Дерево отрезков: просто и быстро
Накануне очередного запуска курса «Алгоритмы для разработчиков» мы провели открытый урок. На нём поговорили об известной идее дерева отрезков, обсудили, как его строить, обновлять и быстро O(log n) вычислять сумму чисел любого отрезка данного массива. Алгоритм очень простой и экономный: нужно O(n) памяти. Для закрепления материала решили олимпиадную задачу.
Вебинар провёл опытный программист и преподаватель, а также руководитель курса «Алгоритмы для разработчиков» Евгений Волосатов.
Присказка
Дерево отрезков — это структура данных, которая позволяет алгоритмически просто и логарифмически быстро находить сумму элементов массива на заданном отрезке.
К примеру, представьте, что надо найти сумму следующих чисел:
При этом нам нужно не просто вычислить сумму чисел указанной последовательности (сумму элементов определённого массива), а максимально быстро найти сумму любой последовательности из этих чисел. То есть мы можем задать какой-нибудь интервал (отрезок) и максимально быстро дать ответ, чему равна сумма чисел из этого интервала:
Что значит быстро? Это значит быстрее, чем, если бы мы просто суммировали числа. Ведь чисел может быть и миллионы, и миллиарды…
Именно желание быстро находить сумму последовательных элементов и стало мотивацией нашего вебинара. Причём, речь идёт не только о сумме, но и о других задачах, например, вычислении любой ассоциативной функции. Таким образом, мы говорим об операциях, выполнение которых не зависит от порядка вычисления.
Возвратимся к нашему ряду:
Очевидно, что если мы хотим находить результат быстро, нужно посчитать некоторые суммы заранее. Первое, что приходит на ум, складывать попарно:
Теперь, если нужно найти сумму чисел, мы можем сделать это практически моментально. Например, чтобы найти сумму упомянутого выше отрезка, достаточно будет 13 прибавить к 9. Всё элементарно: для нахождения суммы четырёх чисел мы сложили только два.
Чтобы найти сумму этого отрезка, нам нужно сложить элементы, которые, так или иначе, покрывают наш отрезок:
Разумеется, 3 + 13 + 19 = 35. Обратите внимание, чтобы найти сумму семи чисел, мы сложили только три. Если бы отрезок состоял из тысячи элементов, достаточно было бы сложить в среднем 10 элементов, так как мы имеем логарифмическую сложность с логарифмом по основанию 2. И это быстро!
Полное двоичное дерево
Полное двоичное дерево — это дерево, у каждого элемента которого есть ровно два дочерних элемента.
Для работы с полным двоичным деревом можно и нужно использовать такую структуру данных, как массив. Нумеровать этот массив удобно с единицы. Пронумеруем каждый элемент двоичного дерева натуральными числами от 1 до 2 n -1:
Вся красота подхода в том, что очень легко вычислять номер детей и родителей.
Формула вычисления «левого ребёнка»: i*2, «правого»: i*2+1.
Например, вычислим номера детей у пятого элемента:
А как от «ребёнка» подняться к «родителю»? Используем целочисленное деление i / 2
Ок, а как определить, левый ребёнок или правый? Ответ следующий: у левых детей чётные номера, у правых — нечётные.
Возвратившись к нашему примеру бинарного дерева, зададимся вопросом, как нам его построить? Смотрите, у нас вначале есть массив чисел:
Для него нужно построить двоичное дерево. Сколько потребуется памяти для хранения двоичного дерева, внизу которого находятся эти элементы?
Ответ на этот вопрос — 2n, если n является степенью двойки.
Идём дальше, ведь перед нами возникают ещё два вопроса:
- с какого элемента необходимо разместить исходные числа в массиве полного двоичного дерева?
- с какого элемента и в какую сторону мы начнём заполнять наше дерево предварительно рассчитанными суммами?
Ответить на первый вопрос достаточно просто: у нас 8 элементов, всего в массиве будет 16 элементов, значит, первый элемент будет под номером 16 — 8 = 8. И начинать строить мы будем слева-направо и снизу-вверх, начиная с 7 элемента, складывая значения у детей, вот так:
Далее необходимо определить, как именно находить сумму нужного отрезка. Вернёмся к нашему первому примеру, пронумеруем элементы и зададим отрезок, причём обозначим первый элемент в отрезке, который нужно сложить, буквой L, а последний — R:
Теперь необходимо ввести ещё одно понятие, чтобы был ясен алгоритм действий. Речь идёт о понятии фундаментальных элементов и соответствующих им фундаментальных отрезков. Фундаментальный элемент — это какой угодно элемент из всего массива, и ему соответствует фундаментальный отрезок, то есть те элементы из начального массива, которые являются его непосредственными детьми/внуками. Для фундаментального элемента с номером 4 “5” фундаментальный отрезок будет с 8 по 9 элемент: [“2”; “3”]:
Что касается фундаментального элемента с номером 10 — “7” (мы обозначили его L), он совпадает со своим фундаментальным отрезком. Можно ли расширить этот фундаментальный отрезок, не выходя за пределы L-R? В нашем случае можно. Правило для левой границы такое: если это левый ребёнок, то фундаментальный отрезок можно расширить, новый фундаментальный элемент будет являться родителем текущего. То есть мы можем в программе писать следующее:
Теперь перейдём к правому элементу R. Он является фундаментальным элементом и левым ребёнком, поэтому расширить область мы уже не можем (выйдем за пределы отрезка). Значит, можем добавить этот элемент к ответу:
Далее нужно, чтобы левый элемент двигался к правому, а правый — к левому. Для левого элемента с индексом L = 10 следующий индекс равен 5, т. к. он пойдёт к родителю. Но пойдёт сначала вправо, а потом вверх:
Итак, значение L перешло на уровень выше и немного правее. Как же будет уменьшаться R? С помощью формулы (R – 1) / 2.
Вот такой алгоритм. Что касается следующих значений переменных L и R, то далее они будут перемещаться следующим образом:
Если же в дереве будет не 8 элементов, а неудобное число, скажем 12, нам придётся дополнить дерево (двоичное дерево должно быть полным) до 16-ти.
Формула для вычисления количества элементов (берётся целая часть логарифма):
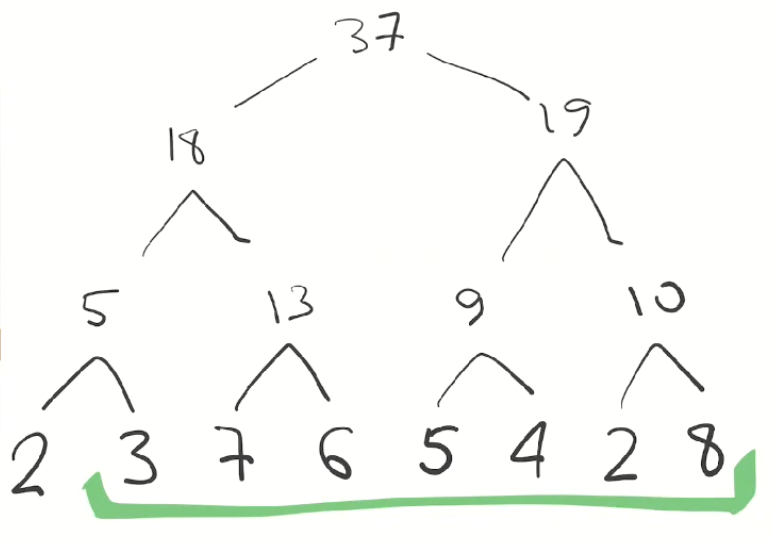
Теперь вычислим ассоциативную функцию нахождения минимума. Вот наше дерево и отрезок:
Как думаете, сколько раз в нашей функции будет задействован элемент № 5 — один или два? Разумеется, один, но каким образом это проверяется в алгоритме? На самом деле, этот элемент является либо левым, либо правым сыном, а значит, выполнится действие либо для L, либо для R.
+
Теперь рассмотрим операцию изменения. Допустим, изменился какой-нибудь элемент, например, вместо 7 пришёл 0. Чтобы наше дерево отрезков осталось в рабочем состоянии, необходимо обновить всех родителей, причём нужно идти до самого верха.
Решение олимпиадной задачи
Одно из требований к таким задачам — всё должно работать быстро. Итак, имеем следующее условие:
Будем решать её, используя знания о дереве отрезков. В результате получим следующий код на C#:
Отправляем на проверку, видим, что решение принято и является полным, а значит, наш алгоритм работает.
На этом всё, если хотите подробностей, смотрите видео целиком. Также можете на досуге почитать следующие авторские статьи нашего преподавателя Евгения Волосатова на Хабре:
Источник
Персистентные деревья отрезков
Структуры данных можно разделить на две группы: эфемерные (ephemeral) и персистентные (persistent).
Эфемерными называются структуры данных, хранящие только последнюю свою версию.
Персистентные структуры, то есть те, которые сохраняют все свои предыдущие версии, в свою очередь можно разделить еще на две подгруппы: если структура данных, позволяет изменять только последнюю версию, она называется частично персистентной (partially persistent), если же позволяется изменять любую версию, такая структура считается полностью персистентной (fully persistent).
Далее будет рассмотрено дерево отрезков и его полностью персистентная версия.
Весь код доступен на GitHub.
Дерево отрезков
Те, кто уже знаком с деревьями отрезков, могут сразу перейти к разделу о персистентной версии.
Деревом отрезков называется структура данных, позволяющая для данного массива A быстро выполнять следующие операции:
Описание
Пусть n — длина массива A , будем заполнять его нейтральными элементами до тех пор, пока его длина не станет равна степени двойки (например, если f — сумма, массив будет дополняться нулями).
Теперь построим такое двоичное дерево, что его листьями будут все элементы A и глубина всех листьев одинакова, а во всех остальных вершинах будут храниться значения f от значений дочерних вершин.
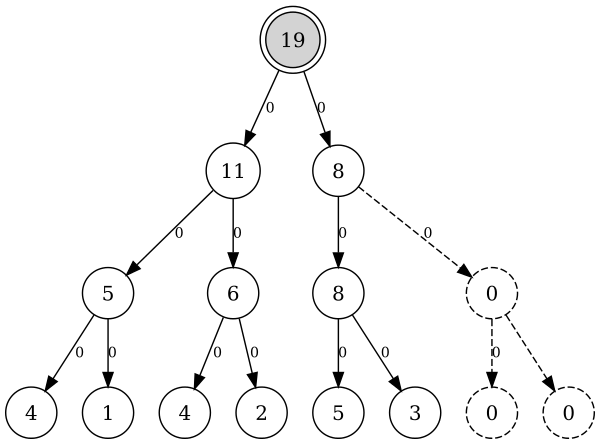
Рассмотрим в качестве примера дерево отрезков для массива A = [4, 1, 4, 2, 5, 3] :
Хранить такое дерево удобно как и двоичную кучу: в виде массива вершин, записанных подряд сверху вниз слева направо:
19 11 8 5 6 8 0 4 1 4 2 5 3 0 0
В таком случае для вершины с индексом i ее предком будет вершина ((i — 1) / 2) , а левый и правый дочерние вершины будут иметь индексы (2 * i + 1) и (2 * i + 2) соответственно (считая, что элементы в массиве нумеруются с нуля).
Построение
Удобно строить дерево отрезков рекурсивно сверху вниз: для каждой вершины построить левую и правую дочерние вершины, после чего посчитать значение f от их значений, а для листов же просто записать соответствующее значение массива в дерево.
Строя дерево таким образом каждая вершина будет посещена один раз, и, так как количество вершин в дереве Θ(n), сложность построения также Θ(n).
Изменение
После того, как было изменено значение какого-либо элемента, в дереве могли испортиться некоторые из значений предков данного элемента. Исправить это можно, пересчитав значения предков данного элемента, поднимаясь по дереву снизу вверх.
Например, если в массиве A заменить A[3] на 10 , то будут пересчитаны вершины со значениями 6 , 11 и 19 .
Так как высота дерева log n, то операция изменения затронет ровно log n вершин, значит, асимптотика операции O(log n).
Вычисление F
Данная операция будет выполняться рекурсивно сверху вниз.
Пусть в произвольной вершине v посчитано F для диапазона l..r , тогда нетрудно проверить, что в левой дочерней вершине посчитано значение F для l..((l + r) / 2) , а в правой — для ((l + r) / 2 + 1)..r .
Предположим, что поступил запрос F(i, j) , и текущая вершина — v . Возможны два случая:
- В узле v уже посчитано значение F(i, j) . Тогда ответом на полученный запрос будет значение вершины v .
- В узле v записано F для большего диапазона. В таком случае рекурсивно вызовем вычисление F(i, (l + r) / 2) для левого дочерней вершины и F((l + r) / 2 + 1, j) для правой, и ответом будет f от этих двух значений.
Пример
Персистентное дерево отрезков
Добиться персистентности можно разными способами, самый простой из них — при каждом изменении делать полную копию старой версии и изменять ее, как обычное дерево отрезков, однако такой способ слишком затратен по памяти и ухудшает асимптотику операции Change до O(n).
Построение
Построение персистентного дерева отрезков будет аналогично построению обычного дерева отрезков за исключением того, что теперь для каждой вершины дополнительно придется в явном виде хранить ссылки на дочерние вершины.
Также дополнительно понадобится хранить массив вершин, являющихся корнями в соответствующих версиях дерева. При построении в него добавляется единственная вершина, являющаяся корнем полученного дерева.
Так как единственное изменение по сравнению с эфемерным деревом отрезков — это добавление информации о левой и правой дочерних вершинах, сложность построения осталось неизменной, то есть Θ(n).
Изменение
Вместо полного копирования дерева при изменении вершины к нему будут добавлены только те вершины, которые должны были измениться, и вместо изменения значений старых вершин, пересчитанные значения будут сохранены в новые. Все новые вершины будут ссылаться на одну вершину из дерева старой версии и на одну из только что добавленных.
Добавление новой ветки делается аналогично построению всего дерева за исключением того, что вместо построения двух дочерних вершин, новая вершина строится только в том направлении, в котором лежит измененная вершина.
После этого обновляется массив корневых вершин.
Так как при изменении только добавляется log n вершин, асимптотика операции — O(log n).
Вычисление F
Вычисление F производится аналогично эфемерному дереву. Единственные отличия: переходы к дочерним вершинам и запуск из разных корневых вершин.
Отсюда следует сложность O(log n).
Пример
Задачи
При помощи персистентного дерева отрезков можно решить задачу «Откат» (разбор задачи). Решение задачи с использованием приведенной выше реализации персистентного дерева отрезков доступно на GitHub.
Также здесь можно прочитать обсуждение задачи о k-ой порядковой статистике на диапазоне.
Источник


















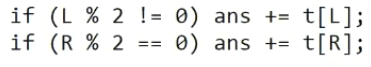




![Дерево отрезков для массива [4, 1, 4, 2, 5, 3]](https://habrastorage.org/storage2/549/053/b2f/549053b2f992ca7dae0fd0f6013b51ed.png)
![Персистентное дерево отрезков, версия 1 (A[3] = 10)](https://habrastorage.org/storage2/0c8/68b/0aa/0c868b0aa3d58afe2ef715d1b0f6c18e.png)