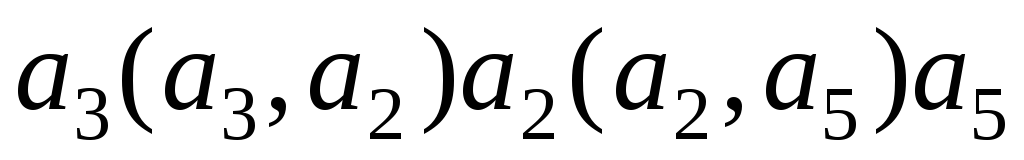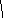Остовное дерево связного графа
Деревом называется связный граф без контуров (а значит, и без циклов). Граф (несвязный), состоящий из нескольких деревьев иногда называют лесом.
Напомним, что вершина в графе называется висячей, если ее степень равна единице. Дерево должно обязательно иметь висячую вершину, так как если бы степень всех вершин в дереве была бы больше или равна 2, то по самой первой лемме граф должен иметь цикл, что противоречит определению дерева.
Докажем сейчас следующую достаточно важную теорему.
Теорема. Если граф G является деревом, то число его ребер (т) и число его вершин (п) связаны соотношением т = п – 1.
Доказательство этой теоремы проведем по индукции по числу вершин. Если данный граф содержит всего 2 вершины, то в нем только 1 ребро, и нужное соотношение выполнено. Пусть наше утверждение выполнено для любого дерева, число вершин которого строго меньше п, Докажем его для дерева G, содержащего п вершин. Возьмем висячую вершину дерева G и удалим ее из графа (вместе с единственным ребром, выходящим из этой вершины). Тогда новый граф также является деревом: новый граф не содержит контуров (циклов), он остается связным. (Если бы новый граф оказался несвязным, то какие-то две вершины графа G были бы связаны между собой через удаленную (висячую) вершину. В этом случае степень этой висячей вершины была бы больше или равна 2, что невозможно). Таким образом, новый граф является деревом, и по индукционному предположению для него число ребер меньше числа вершин на единицу. Так как число вершин и число ребер нового графа отличается от числа вершин и ребер “старого” графа G на единицу, то для графа G также выполнено то же самое соотношение. Таким образом, индукция проведена, и теорема доказана.
На самом деле верно и обратное утверждение, которое является частью более общей теоремы, отражающей простейшие свойства дерева.
Теорема. Следующие 4 условия равносильны:
число ребер (т) и число вершин в графе (п) связаны соотношением т = п – 1;
любые две вершины в графе могут быть связаны (простым) путем, и этот путь единствен;
граф G связен и не содержит контуров.
Заметим, что генеалогическое дерево (в котором вершины графа – это некоторый человек и его прямые предки, а смежные вершины – это люди, связанные родством: мать и ее ребенок или отец и его ребенок) деревом в смысле теории графов не является (так как оно обязательно должно содержать циклы: некоторые предки данного человека должны иметь общего предка).
Однако игры с полной информацией (т. е. игры, не имеющие вероятностного характера: шахматы, шашки, уголки и т. д.) могут быть изображены в виде дерева. Именно поэтому такого типа игры допускают возможность применения компьютеров даже для решения теоретических вопросов этих игр.
Остовное дерево
Деревом называется связный неориентированный граф без циклов.
Существует ещё несколько разновидностей определения дерева:
1. Дерево — это связный граф, у которого число рёбер на 1 меньше числа вершин.
2. Дерево — это связный граф, любые две вершины коотрого соеденены единственной цепью.
3. Дерево — это граф, не содержащий циклов, такой, что при добавлении нового ребра, получаем ровно один цикл.
Остовным деревом неориентированного графа G будем называть его подграф DНG, содержащий все его вершины и являющийся деревом.
Остовное дерево D нагруженного графа G(V,Q,W) называется минимальным, если сумма весов всех его рёбер минимальна по сравнению с другими остовными деревьями.
Остовное дерево связного графа
Определение. Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.
Определение. Число m(G)-n(G)+1 называется цикломатическим числом связного графа G и обозначается через v(G).
Замечание. Понятие остовного дерева и цикломатического числа аналогичным образом определяется и для произвольного связного псевдографа G.
Покажем существование остовного дерева для произвольного связного псевдографа G=(V,X), описав алгоритм его выделения.
Шаг 1. Выбираем в G произвольную вершину u1, которая образует подграф G1 псевдографа G, являющийся деревом. Полагаем i=1.
Шаг 2. Если i=n, где n=n(G), то задача решена, и Gi – искомое остовное дерево псевдографа G. В противном случае переходим к шагу 3.
Шаг 3. Пусть уже построено дерево Gi, являющееся подграфом псевдографа G и содержащий некоторые вершины u1, …, ui, где 1didn-1. Строим граф Gi+1, добавляя к графу Gi новую вершину ui+1О V, смежную в G с некоторой вершиной uj графа Gi, и новое ребро (ui+1, uj) (в силу связности G и того обстоятельства, что i < n, указанная вершина ui+1 обязательно найдется). Согласно утверждению граф Gi+1 также является деревом. Присваиваем i:=i+1 и переходим к шагу 2.
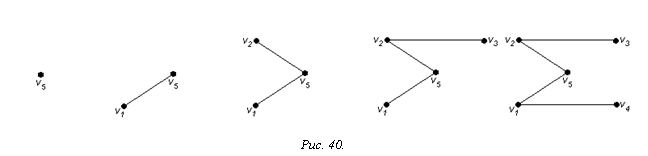
Используя алгоритм, выделим остовное дерево графа G, изображенного на рисунке 39.
На рисунке 40 приведена последовательность графов Gi, i=1, 2, 3, 4, 5, получаемых в результате выполнения алгоритма.
При этом в силу того, что n(G)=5, G5 — остовное дерево графа G.
Замечание. Остовное дерево связного графа может быть выделено, вообще говоря, не единственным способом.
Общее число остовных деревьев связного графа может оказаться весьма большим. Например, для полного графа с n вершинами оно равно nn-2.
В общем случае обозначим через G произвольный граф с n вершинами, m ребрами и k компонентами. Как уже было сказано, применяя выше описанный алгоритм, получим в результате граф, являющийся остовным лесом.
Определение. Число ребер, удаленных при построении остовного леса произвольного графа G, называется цикломатическим числом (или цикломатическим рангом) графа G и обозначается через g (G) = m – n + k.
Циклический ранг дерева равен нулю, а циклический ранг циклического графа равен единице.
Определение. Коциклическим рангом графа G называется число ребер в его остовном дереве.
С понятием остовного леса Т графа G тесно связано понятие фундаментальной системы циклов, ассоциированной с Т.
Определение. Если добавить к Т любое не содержащиеся в нем ребро графа G, то получим единственный цикл; множество всех циклов, получаемых таким способом (т.е. путем добавления по отдельности каждого ребра из G, не содержащегося в Т), называется фундаментальной системой циклов, ассоциированной с Т.
Источник
Пути. Циклы. Цепи в графах
Пусть G = (V, E) некоторый граф. Путем (маршрутом) в графе G, соединяющим вершины v1 и vn, называется любая чередующаяся последовательность вершин и ребер вида v0,e 0,v1,e1,v2,e 2…vn-1,e n-1,vn, в которой каждое ребро ei инцидентно вершинам vi и vi+1.
Путь называется замкнутым, если его начальная и конечная вершины совпадают.
Путь называется цепью, если все его ребра различны.
Цепь называется простой, если все ее вершины различны.
Замкнутая цепь называется циклом.
Цикл называется простым, если его вершины не повторяются.
Вот схематическое изображение простого цикла:
А вот схематическое изображение цикла, не являющегося простым:
Для пути v0, e 0 ,v1, e1 , ….vn число ребер n называется длиной пути.
Две вершины графа могут быть связаны некоторым путем: их называют связанными. Например, в графе
a
a2 a3 . a4
вершины a3 и a5 связаны (путем ), а вершины a4 и a1 нет.
Простой граф – это граф, не содержащий петель и кратных ребер.
Граф называется связным, если для любой пары его вершин существует соединяющая их простая цепь. Т.о. граф связен, если из любой его вершины можно прийти к любой другой. Таким образом, выше приведен пример графа несвязного. Связной компонентой графа называется такой его подграф, который является сам по себе графом связным и при этом совпадающим с любым другим содержащим его связным подграфом. Таким образом, связный граф обладает единственной связной компонентой — это он сам. А вот пример графа с тремя связными компонентами (имена вершин не имеют значения):

Компонентой связности графа называется максимальный (по числу вершин и ребер) связный подграф этого граф.
Каждый граф или сам является компонентой связности или распадается на компоненты. Граф, содержащий хотя бы две компоненты связности, называется несвязным. Связный граф состоит из одной компоненты связности.
Граф называется эйлеровым, если он содержит цикл, проходящий через все ребра этого графа по одному разу. Такой цикл называется эйлеровым циклом.
Вот пример эйлерова графа:

А вот пример графа, не являющегося эйлеровым:

Во многих задачах, решаемых с использованием графов, требуется проложить маршрут от одной вершины графа к другой или обойти все его вершины, учитывая те или иные ограничения.
Смысл такой задачи на интуитивном уровне ясен, но требуется уточнить понятия, используемы при решении подобного рода задач.
Прежде всего, уточним термины «маршрут», «цепь», «цикл» и «путь». Эти четыре понятия находятся в следующем соотношении: пути и циклы – это особые виды цепей, цепь – особый вид маршрута.
Маршрут – это последовательность вершин и ребер графа, следуя по которым, можно попасть из одной его вершины в другую.
Цепь – это маршрут без повторяющихся ребер.
Путь – это цепь, все вершины которой (за исключением, быть может, начальной и конечной) различны.
Цикл – это цепь, у которой совпадают начальная и конечная вершины, а все остальные различны.
Можно составить следующие маршруты из А в С в графе G:
М2: А – е2 – Е – е6 – Д – е7 – Д – е6 – Е – е5 – С (не цепь);
М3: А – е1 – B – е3 – C – е5 – Е – е4 – С (цепь, но не путь).
А – е1 – В – е3 – С – е4 – Е – е2 – А;
Граф называют связным, если из каждой его вершины существует путь в любую другую его вершину. Граф, рассмотренный в примере, является, связным. Если удалить из него ребро , то он потеряет связность и распадется на компоненты: одна из компонент будет содержать вершину Д и петлю , вторая компонента – вершины А,В,С,Е, связанные между собой всеми оставшимися ребрами.
Для представления данных в алгоритмах на дискретных структурах часто используются графы, которые называются деревьями.
Деревом называют связный неорграф, не содержащий циклов.
На рис. 6.8 показано, так называемое, корневое дерево. Одна из вершин корневого дерева (вершина 1) выделена, ее называют корнем дерева. Оставшиеся вершины разбиты на поддеревья (поддерево с вершинами 2,5,6 и поддерево 4,7,8,9). Вершины 5,6,3,7,8,9 называют листьями дерева. Несвязный неорграф, компонентами которого являются деревья, называют лесом.
Если граф связный, но не является деревом, в нем всегда можно выделить часть, включающую все вершины и образующую дерево. Такую часть графа называют остовом графа. Если граф несвязен, то можно превратить в дерево каждую его компоненту. Полученная совокупность деревьев носит название остовного леса.
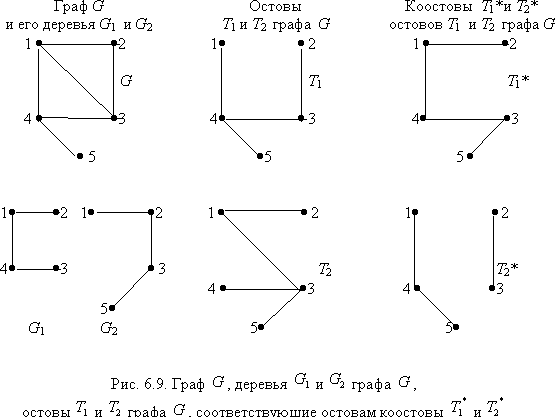
Вообще говоря, в графе можно выделить несколько различных остовов. Каждый из них будет являться деревом, включающим все вершины графа, а следовательно, число ребер любом из остовов будет на единицу меньше числа вершин графа. Если выделен какой-либо остов, то все ребра графа, не вошедшие в этот остов, образуют коостов, соответствующий данному остову.
Остовным деревом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пусть G связный граф. Тогда остовное дерево графа G (если оно существует) должно содержать n(G) – 1 ребер. Таким образом, любое остовное дерево графа G есть результат удаления из G ровно m(G)-(n(G)-1)=m(G)-n(G)+1 ребер.
На рис. 6.9 показан пример выделения деревьев, остовов и коостовов из графа .
Источник