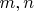Главная » Деревья

Дерево примитивных пифагоровых троек

Содержание
  1. Древовидная структура примитивных пифагорейских троек
  2. содержание
  3. доказательства
  4. Существование только примитивных пифагорейских троек
  5. Сохранение пифагорейской собственности
  6. Сохранение первобытности
  7. Наличие каждой примитивной пифагорейской тройки ровно один раз
  8. характеристики
  9. Альтернативные методы построения дерева
  10. Другое дерево
  11. Индивидуальные доказательства
  12. Научный форум dxdy

Древовидная структура примитивных пифагорейских троек

В математике , то дерево примитивных пифагорейских троек данных дерево , в котором каждый узел переходит к трем последующим узлам, бесконечное множество всех узлов получают все (и только) примитивные пифагорейские тройки без дубликатов.

Пифагорова тройка — это набор из трех положительных целых чисел a, b и c, каждое из которых может быть длинами сторон прямоугольного треугольника, таким образом удовлетворяя уравнению . Тройка считается примитивной тогда и только тогда, когда наибольший общий делитель a, b и c равен единице. Примитивные тройки Пифагора (a, b, c) даже попарно взаимно просты . Множество всех примитивных пифагоровых троек естественно имеет структуру корневого дерева , особенно тройного дерева. Впервые это было обнаружено Б. Берггреном в 1934 году. а 2 + б 2 знак равно c 2 + b ^ = c ^ >

FJM Barning показал следующее: Если какая-либо из следующих матриц

А. знак равно [ 1 — 2 2 2 — 1 2 2 — 2 3 ] Б. знак равно [ 1 2 2 2 1 2 2 2 3 ] С. знак равно [ — 1 2 2 — 2 1 2 — 2 2 3 ] A = 1 & -2 & 2 \\ 2 & -1 & 2 \\ 2 & -2 & 3 \ end > & B = 1 & 2 & 2 \\ 2 & 1 & 2 \\ 2 & 2 & 3 \ end > & C = -1 & 2 & 2 \\ — 2 & 1 & 2 \\ — 2 & 2 & 3 \ end > \ end >>

умножается справа на вектор-столбец , компоненты которого образуют пифагорову тройку , тогда результатом является другой вектор-столбец, компоненты которого образуют еще одну пифагорову тройку. Если исходная тройка примитивна, результирующая тройка также примитивна. Таким образом, каждая примитивная пифагорейская тройка имеет трех «детей». Таким образом, все примитивные тройки Пифагора являются производными от тройки (3, 4, 5), и никакая примитивная тройка не появляется более одного раза. Результат можно представить графически в виде бесконечного троичного дерева с (3, 4, 5) в качестве корневого узла (см. Классическое дерево справа). Это дерево также появилось в работах А. Холла в 1970 г. и А. Р. Канги в 1990 г. В 2008 г. В. Е. Фирстов в целом показал, что существует только три таких дерева и явно приводит к дереву, аналогичному дереву Берггрена, но начиная с начального узла (4, 3, 5) .

содержание

доказательства

Существование только примитивных пифагорейских троек

Путем полной индукции можно показать, что дерево содержит примитивные пифагоровы тройки и ничего больше, показав, что, начиная с примитивной пифагоровой тройки (как в начальном узле с (3, 4, 5)), каждая сгенерированная тройка является как Пифагорейский и примитивный.

Сохранение пифагорейской собственности

Если одна из вышеперечисленных матриц, скажем, A , применяется к тройке ( a , b , c ) T со свойством Пифагора, чтобы получить новую тройку ( d , e , f ) T = A ( a , b , c ) T , эта новая тройка тоже пифагорейская. Это можно показать путем записи каждого из д , е, и е в виде суммы трех слагаемых с в , б, и с , а затем возведения в квадрат каждого из них и подставляя для того чтобы получить. Это относится как к B, так и к C, а также к A. а 2 + б 2 знак равно c 2 + b ^ = c ^ > c 2 знак равно а 2 + б 2 <\ displaystyle c ^ = a ^ + b ^ > ж 2 знак равно d 2 + е 2 <\ displaystyle f ^ = d ^ + e ^ >

Читайте также:  1с дерево значений добавить строки

Сохранение первобытности

Матрицы , B и C являются всеми унимодулярными — то есть, они имеют только число записей и их определители ± 1. Таким образом, их инверсии также унимодулярны и, в частности, имеют только целочисленные элементы. Таким образом, если один из них, например, , к примитивной пифагорейской тройки ( в , б , с ) Т применяется, получается дополнительно тройка ( д , е , F ) T . Мы имеем ( d , е , п ) Т = A ( , Ь , гр ) T и ( , Ь , с ) Т = -1 ( д , е , ф ) Т . Если любое простое число делит два (и, следовательно, все три из них) d , e и f , то по этому последнему уравнению это простое число также делит каждое из a , b и c . Таким образом, если a , b и c на самом деле взаимно просты в парах, то d , e и f также должны быть взаимно просты в парах. Это относится как к B, так и к C, а также к A.

Наличие каждой примитивной пифагорейской тройки ровно один раз

Чтобы показать, что дерево содержит каждую примитивную тройку Пифагора, но не более одного раза, достаточно показать, что для такой тройки существует ровно один путь назад через дерево к начальному узлу (3, 4, 5). В этом можно убедиться, последовательно применяя каждую из унимодулярных обратных матриц A −1 , B −1 и C −1 к любой примитивной пифагоровой тройке ( d , e , f ), при этом следует отметить, что из приведенных выше рассуждений примитивность и свойство Пифагора сохраняется, и со ссылкой на тот факт, что для каждой тройки, которая больше, чем (3, 4, 5), ровно одна из матриц обратных переходов приводит к новой тройке со всеми положительными элементами (и меньшей гипотенузой). По индукции эта новая действительная тройка сама по себе приводит ровно к одной действительной тройке меньшего размера и так далее. Из-за конечности числа все меньших потенциальных гипотенуз (3, 4, 5) наконец достигается. Это доказывает, что ( d , e , f ) действительно встречается в дереве, поскольку до него можно добраться из (3, 4, 5), изменив шаги; и это происходит однозначно, потому что существует только один путь от ( d , e , f ) до (3, 4, 5).

характеристики

Преобразование с использованием матрицы A при повторном выполнении на ( a , b , c ) = (3, 4, 5) сохраняет признак ; матрица B сохраняется ; а матрица C сохраняет связь . б + 1 знак равно c | а — б | знак равно 1 а + 2 знак равно c

Геометрическая интерпретация этого дерева включает круги, присутствующие в каждом узле . Три дочерних элемента родительского треугольника «наследуют» свой радиус вписанной окружности от родительского треугольника: радиусы окружности родительского треугольника становятся радиусами вписанной окружности для следующего поколения. Например, родительский треугольник (3, 4, 5) имеет радиусы окружности 2, 3 и 6. Это в точности радиусы вписанной окружности трех дочерних треугольников (5, 12, 13), (15, 8, 17) и ( 21, 20, 29).

Если A или C многократно применяются к пифагоровой тройке, то динамика a , b и c может быть выражена как динамика x в следующем уравнении

Икс п + 3 — 3 Икс п + 2 + 3 Икс п + 1 — Икс п знак равно 0 -3x_ + 3x_ -x_ = 0> ,

Читайте также:  Долларовое дерево пожелтела веточка

который структурно напоминает характеристические многочлены матриц A и C :

λ 3 — 3 λ 2 + 3 λ — 1 знак равно 0 -3 \ lambda ^ +3 \ lambda -1 = 0>

Если B многократно применяется к пифагоровой тройке, динамика a , b и c соответствует динамике x следующим образом

Икс п + 3 — 5 Икс п + 2 — 5 Икс п + 1 + Икс п знак равно 0 -5x_ -5x_ + x_ = 0> ,

что структурно характеристический многочлен B похож.

Кроме того, бесконечное количество разностных уравнений третьего порядка можно найти, умножив три матрицы друг на друга любое количество раз в любом порядке. Например, матрица D = CB перемещает узел в дереве на две позиции (поперек, затем вниз) за один шаг. Характеристический многочлен D обеспечивает образец динамики 3-го порядка a , b или c в дереве, сформированном D.

Альтернативные методы построения дерева

Другой подход к динамике этого дерева основан на стандартной формуле для генерации всех примитивных пифагоровых троек:

а знак равно м 2 — п 2 , -n ^ ,> б знак равно 2 м п , c знак равно м 2 + п 2 , <\ displaystyle c = m ^ + n ^ ,>

с m > n > 0 и m и n взаимно простыми и разной четностью . Пары ( m , n ) можно повторять, умножая одну из следующих матриц на предыдущую пару как вектор-столбец.

Каждое из умножений сохраняет указанное выше неравенство, взаимно простые числа и противоположную четность. Результирующее тернарное дерево — начиная с (2,1) — содержит каждую такую пару ( m , n ) ровно один раз, и когда оно преобразуется в ( a , b , c ), дерево, описанное выше, создается точно.

Другая возможность — с двумя базовыми параметрами для генерации тройного дерева — использует альтернативную формулу для всех примитивных троек:

где u > v > 0, u и v взаимно просты и нечетны. Пары ( u , v ) можно повторять, умножая одну из указанных выше матриц (2 × 2) на предыдущую пару в качестве вектора-столбца. Каждое из умножений сохраняет указанное выше неравенство, взаимно простые числа и то, что оба члена нечетные. Если этот процесс запускается в (3, 1), результирующее троичное дерево содержит каждую такую пару ( u , v ) ровно один раз, и если оно преобразуется в ( a , b , c ), также создается дерево, описанное выше.

Другое дерево

В качестве альтернативы вы можете использовать три другие матрицы, найденные Прайсом. Эти матрицы A ‘, B’, C ‘ :

Соответствующие им линейные преобразования:

+ 2 а + б — c знак равно а 1 — 2 а + 2 б + 2 c знак равно б 1 — 2 а + б + 3 c знак равно c 1 → [ а 1 , б 1 , c 1 ] + 2 а + б + c знак равно а 2 + 2 а — 2 б + 2 c знак равно б 2 + 2 а — б + 3 c знак равно c 2 → [ а 2 , б 2 , c 2 ] + 2 а — б + c знак равно а 3 + 2 а + 2 б + 2 c знак равно б 3 + 2 а + б + 3 c знак равно c 3 → [ а 3 , б 3 , c 3 ] & + 2a + bc = a_ \ quad & -2a + 2b + 2c = b_ \ quad & -2a + b + 3c = c_ & \ quad \ to \ left [> a_ , > b_ , > c_ \ right] \ end > \\ & + 2a + b + c = a_ \ quad & + 2a-2b + 2c = b_ \ quad & + 2a-b + 3c = c_ & \ quad \ to \ left [> a_ , > b_ , > c_ \ right] \ end > \ \ & + 2a-b + c = a_ \ quad & + 2a + 2b + 2c = b_ \ quad & + 2a + b + 3c = c_ & \ quad \ to \ left [> a_ , > b_ , > c_ \ right] \ end > \\ & \ конец >>

Читайте также:  Симметричный обход дерева алгоритм

Три дочерних элемента, сгенерированные каждым из двух наборов матриц (Берггрена и Прайса), не совпадают, но каждый набор отдельно генерирует все примитивные тройки. Например, если вы используете (5, 12, 13) в качестве родительского триплета, вы получите два предложения с тремя дочерними элементами в каждом:

[ 5 , 12-е , 13-е ] А. Б. С. [ 45 , 28 год , 53 ] [ 55 , 48 , 73 ] [ 7-е , 24 , 25-е ] [ 5 , 12-е , 13-е ] А. ′ Б. ′ С. ′ [ 9 , 40 , 41 год ] [ 35 год , 12-е , 37 ] [ 11 , 60 , 61 ] & \ left [5,12,13 \ right] & \\ A & B & C \\\ left [45,28,53 \ right] & \ left [55 , 48,73 \ right] & \ left [7,24,25 \ right] \ end > \ quad \ quad \ quad \ quad \ quad \ quad <\ begin & \ left [ 5,12, 13 \ вправо] & \\ A '& B' & C '\\\ влево [9,40,41 \ вправо] и \ влево [35,12,37 \ вправо] и \ влево [11, 60,61 \ right] \ end >>

Индивидуальные доказательства

  1. ↑ Б. Берггрен, Pytagoreiska trianglar (на шведском языке), Elementa: Tidskrift för elementär matematik, fysik och kemi 17 (1934), 129-139. См. Стр. 6 для корневого дерева.
  2. ↑ Барнинг, FJM (1963), Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices (на голландском языке), Math. Centrum Amsterdam Afd. Zuivere Wisk. ZW-011: 37, ir.cwi.nl .
  3. ↑ A. Холл, Генеалогия пифагорейских триад, The Mathematical Gazette , том 54, номер 390, декабрь 1970 г., страницы 377-9.
  4. ↑ Канга, А.Р., Генеалогическое древо троек Пифагора, Бюллетень Института математики и его приложений 26, январь / февраль 1990 г., стр. 15-17.
  5. ↑ Фирстов В. Е. Специальная полугруппа матричных преобразований примитивных пар и генеалогия троек Пифагора , Математические заметки, том 84, номер 2, август 2008 г., страницы 263-279, русский язык; mathnet.ru .
  6. ^ Аб Х. Ли Цена: Дерево Пифагора: Новый вид . С. 7, 25 сентября 2008 г.
  7. ^ Mitchell, Douglas W., связь по 92.60, Математическая газета 93, июль 2009, 358-9.
  8. ^ Роберт А. Сондерс: Возвращение к генеалогическому древу пифагорейских троек . В кн . : Математический вестник . 78, июль 1994 г., стр. 190–193.
  9. ↑ Митчелл, Дуглас В., Альтернативная характеристика всех примитивных пифагорейских троек, Mathematical Gazette 85, июль 2001, 273-275.

Источник

Научный форум dxdy

$m, n$

Есть формула Евклида с параметрами ,
а также способ, который предложили в 1971 г. американские математики Тейган и Хедвин:
ananserr.narod.
Какие ещё есть способы и формулы для генерации всех Пифагоровых троек?

Последний раз редактировалось vicvolf 11.03.2019, 23:01, всего редактировалось 1 раз.

Последний раз редактировалось Soul Friend 14.03.2019, 22:32, всего редактировалось 1 раз.

предлагаю двоичное дерево примитивных троек:
1)метод Евклида $x=m^2-n^2$, $y=2mn$, $z=m^2+n^2$
из неё образуются две примитивные тройки:
2)$x=m^4-n^2$, $y=2m^2n$, $z=m^4+n^2$
3)$x=m^4-n^4$, $y=2m^2n^2$, $z=m^4+n^4$
При желании можно добавить ещё одну ветвь, я так думаю.
Но я сейчас работаю над другим способом, похожий на способ предложенный американцами.

предлагаю двоичное дерево примитивных троек:
1)метод Евклида $x=m^2-n^2$, $y=2mn$, $z=m^2+n^2$
из неё образуются две примитивные тройки:
2)$x=m^4-n^2$, $y=2m^2n$, $z=m^4+n^2$
3)$x=m^4-n^4$, $y=2m^2n^2$, $z=m^4+n^4$
При желании можно добавить ещё одну ветвь, я так думаю

4)$x=n^4-m^2$, $y=2mn^2$, $z=m^2+n^4$
Вуаля, получилось троичное дерево.

Последний раз редактировалось Soul Friend 15.03.2019, 08:12, всего редактировалось 3 раз(а).

4)$x=n^4-m^2$, $y=2mn^2$, $z=m^2+n^4$

здесь правильно будет для $x$так:
$\sqrt<n^8-2m^2n^4+m^4 data-lazy-src=

Источник

Оцените статью
© 2024 Деревья и растения