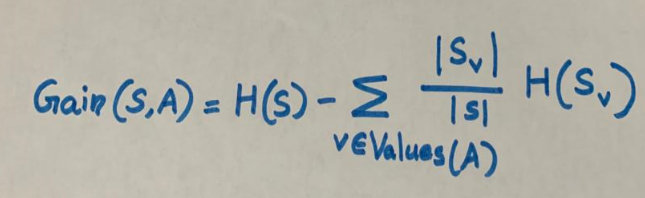Дерево принятия решений энтропия

Машинное обучение 101-ID3 Деревья принятия решений и вычисление энтропии (1)

Энтропия, известная как контроллер дерева решений, решающая, где разделить данные. Алгоритм ID3 использует энтропию для вычисления однородности образца. Если образец полностью однороден, энтропия равна нулю, а если образец разделен поровну, он имеет энтропию, равную единице [1].

Энтропия n-класса — ›E (S) = ∑ — (pᵢ * log₂pᵢ)

2-х классная энтропия: (S) = — (p₁ * log₂p₁ + p₂ * log₂p₂)

Ex-1:

p₁ = 9 / (9 + 5) = 9/14 (вероятность попадания выборки в один обучающий класс с классом 1)

p₂ = 5/14 (вероятность попадания образца в один учебный класс с классом 2)

E = — (9/14 * log₂ (9/14) + (5/14) * log₂ (5/14))

Получение информации

Границы корня, узлов и листьев определяются приростом информации (IG).

Усиление (S, A) = E (до) — G (после_разбиения)

Примечание. Вы можете найти ID3 как C4.5 в WEKA Tool.

Сначала выберите функцию, которая наиболее точно разделит всю таблицу. Для этого необходимо определить функцию, которая дает наибольший выигрыш.
Значения для 10 примеров тренировок делятся следующим образом:
* 6 Кино
* 2 Теннис
* 1 Хаус * 1 Покупки
Значение энтропии должно быть рассчитано на основе этих значений для начала определения корневого объекта.

E (S) = — ((6/10) * log2 (6/10) + (2/10) * log2 (2/10) + (1/10) * log2 (1/10) + (1/10 ) * log2 (1/10))

Вычисляя значения усиления для всех отдельных объектов, объекты с наибольшим значением усиления выбираются в качестве корневого узла:

Прирост (S, Погода) =?

Солнечный = 3 (1 кино + 2 теннис)

Windy = 4 (3 кинотеатра + 1 покупка)

Rainy = 3 (2 кинотеатра + 1 дом)

Энтропия (S солнечный) = — (1/3) * log2 (1/3) — (2/3) * log2 (2/3) = 0,918

Энтропия (S ветрено) = — (3/4) * log2 (3/4) — (1/4) * log2 (1/4) = 0,811

Энтропия (S дождливый) = — (2/3) * log2 (2/3) — (1/3) * log2 (1/3) = 0,918

Прирост (S, Погода) = 1,571 — (((1 + 2) / 10) * 0,918 + ((3 + 1) / 10) * 0,811 + ((2 + 1) / 10) * 0,918)

Прирост (S, Погода) = 0,70

Gain (S, Parental_Availability) =?

Нет = 5 (2 тенниса + 1 кинотеатр + 1 магазин + 1 дом)

Энтропия (S да) = — (5/5) * log2 (5/5) = 0

Энтропия (S нет) = — (2/5) * log2 (2/5) -3 * (1/5) * log2 (1/5) = 1,922

Прирост (S, родительская_доступность) = энтропия (S) — (P (да) * энтропия (S да) + P (нет) * энтропия (S нет))

Прирост (S, родительская_доступность) = 1,571 — ((5/10) * энтропия (S да) + (5/10) * энтропия (S нет))

Прирост (S, родительская_доступность) = 0,61

Богатые = 7 (3 кинотеатра + 2 тенниса + 1 магазин + 1 дом)

Прирост (S, богатство) = энтропия (S) — (P (богатый) * энтропия (S богатый) + P (бедный) * энтропия (S бедный))

Прирост (S, богатство) = 0,2816

Наконец, все значения усиления перечисляются одно за другим, и в качестве корневого узла выбирается объект с наибольшим значением усиления. В этом случае погода имеет наибольшее значение усиления, поэтому она будет корнем.

Прирост (S, Погода) = 0,70

Прирост (S, Родительская_доступность) = 0,61

Прирост (S, богатство) = 0,2816

Как показано в приведенном выше примере, после выбора корня каждое из отдельных значений функций определяется как листья, и на этот раз набор данных настраивается с этими отдельными значениями. Другими словами, приведенная выше таблица была преобразована в отдельный набор данных, показывающий значения, которые могут принимать другие функции, если погода солнечная. Таким образом, при солнечной погоде, согласно этой таблице, возможные классы интер узла будут следующими:

Энтропия (S солнечный) = — (1/3) * log2 (1/3) — (2/3) * log2 (2/3) = 0,918

Усиление (S солнечно, Parental_Availability) =?

Прирост (S солнечно, Parental_Availability) = энтропия (S солнечно) — (P (да | S солнечно) * энтропия (S да) + P (нет | S солнечно) * энтропия (S нет))

Энтропия (S да) = — (1/3) * log2 (0) — 0 = 0

Энтропия (S нет) = — (2/3) * log2 (0) — 0 = 0

Прирост (S солнечно, Родительская_доступность) = 0,928 — ((1/3) * 0 + (2/3) * 0) = 0,928

Прирост (S солнечно, богатство) = 0,918 — ((3/3) * 0,918 + (0/3) * 0) = 0

Поскольку усиление функции Parental_Availability больше, лист состояния Sunny будет Parental_Availability. В соответствии с набором данных для солнечных условий, если да, будет выбрано Кино, а если нет, то будет выбрано Теннис:

Когда те же расчеты будут выполнены для ветреной и дождливой ситуаций, окончательное дерево решений будет завершено.

Переоснащение

• Это превращение обучения в запоминание.
• График производительности таков, что через определенный момент прирост производительности прекращается и начинает уменьшаться.
• Когда у вас высокий уровень успешности тренировок, но наоборот — результативность тестов, это пример переобучения.
• Более того, если в наших данных есть зашумленная выборка, это может привести к переобучению.
• Когда дерево становится слишком большим, результат получается почти для каждой возможной ветви, что приводит к переоснащению.

Чтобы избежать переобучения, необходимо обрезать дерево либо когда оно растет, либо после того, как дерево сформируется.

Источник

Как разобраться в дереве принятия решений и сделать его на Python

Совсем скоро, 20 ноября, у нас стартует новый поток «Математика и Machine Learning для Data Science», и в преддверии этого мы делимся с вами полезным переводом с подробным, иллюстрированным объяснением дерева решений, разъяснением энтропии дерева решений с формулами и простыми примерами, вводом понятия «информационный выигрыш», которое игнорируется большинством умозрительно-простых туториалов. Статья рассчитана на любящих математику новичков, которые хотят больше разобраться в работе дерева принятия решений. Для полной ясности взят совсем маленький набор данных. В конце статьи — ссылка на код на Github.

Дерево решений — тип контролируемого машинного обучения, который в основном используется в задачах классификации. Дерево решений само по себе — это в основном жадное, нисходящее, рекурсивное разбиение. «Жадное», потому что на каждом шагу выбирается лучшее разбиение. «Сверху вниз» — потому что мы начинаем с корневого узла, который содержит все записи, а затем делается разбиение.

Корневой узел — самый верхний узел в дереве решений называется корневой узел.
Узел принятия решения — подузел, который разделяется на дополнительные подузлы, известен как узел принятия решения.

Лист/терминальный узел — узел, который не разделяется на другие узлы, называется терминальный узел, или лист.

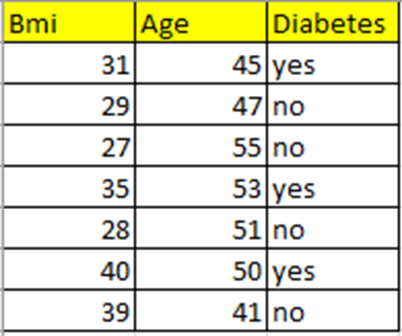
Набор данных

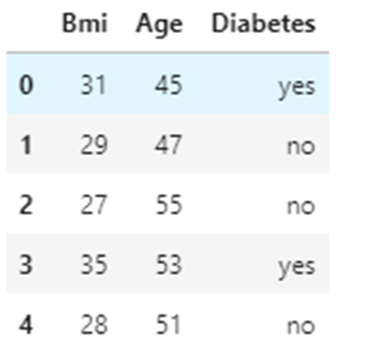
Я взяла совсем маленький набор данных, содержащий индекс массы тела (BMI), возраст (Age) и целевую переменную Diabetes (диабет). Давайте спрогнозируем, будет у человека данного возраста и индекса массы тела диабет или нет.

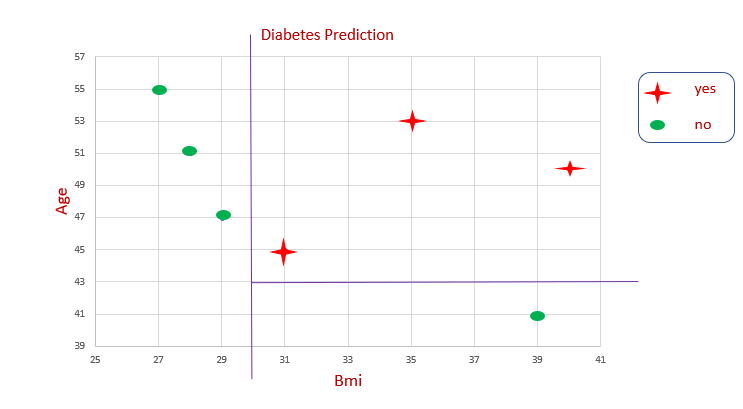
Представление набора данных

На графике невозможно провести какую-то прямую, чтобы определить границу принятия решения. Снова и снова мы разделяем данные, чтобы получить границу решения. Так работает алгоритм дерева решений.

Вот так в дереве решений происходит разбиение.

Важные теоретические определения

Энтропия

Энтропия — это мера случайности или неопределенности. Уровень энтропии колеблется от 0 до 1 . Когда энтропия равна 0, это означает, что подмножество чистое, то есть в нем нет случайных элементов. Когда энтропия равна 1, это означает высокую степень случайности. Энтропия обозначается символами H(S).

Формула энтропии

Энтропия вычисляется так: -(p(0) * log(P(0)) + p(1) * log(P(1)))

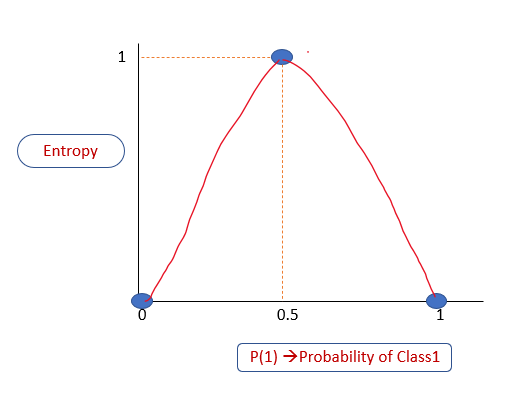
Связь между энтропией и вероятностью

Когда энтропия равна 0, это означает, что подмножество «чистое», то есть в нем нет энтропии: либо все «да», либо все голоса «нет». Когда она равна 1, то это означает высокую степень случайности. Построим график вероятности P(1) вероятности принадлежности к классу 1 в зависимости от энтропии. Из объяснения выше мы знаем, что:

Если P(1) равно 0, то энтропия равна 0
Если P(1) равно 1, то энтропия равна 0
Если P(1) равно 0,5, то энтропия равна 1

Уровень энтропии всегда находится в диапазоне от 0 до 1.

Информационный выигрыш

Информационный выигрыш для разбиения рассчитывается путем вычитания взвешенных энтропий каждой ветви из исходной энтропии. Используем его для принятия решения о порядке расположения атрибутов в узлах дерева решений.

Как работает дерево решений

В нашем наборе данных два атрибута, BMI и Age. В базе данных семь записей. Построим дерево решений для нашего набора данных.

1. Корневой узел

В дереве решений начнем с корневого узла. Возьмем все записи (в нашем наборе данных их семь) в качестве обучающих выборок.

В корневом узле наблюдаем три голоса за и четыре против.
Вероятность принадлежности к классу 0 равна 4/7. Четыре из семи записей принадлежат к классу 0.
P(0) = 4/7
Вероятность принадлежности к классу 1 равна 3/7. То есть три из семи записей принадлежат классу 1.
P(1) = 3/7.

Вычисляем энтропию корневого узла:

2. Как происходит разбиение?

У нас есть два атрибута — BMI и Age. Как на основе этих атрибутов происходит разбиение? Как проверить эффективность разбиения?

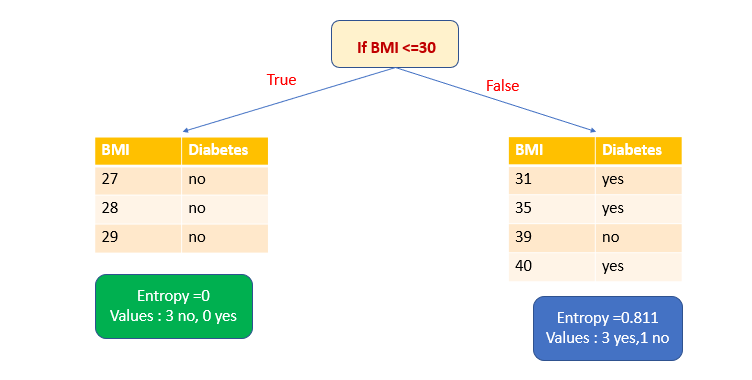
1. При выборе атрибута BMI в качестве переменной разделения и ≤30 в качестве точки разделения мы получим одно чистое подмножество.

Точки разбиения рассматриваются для каждой точки набора данных. Таким образом, если точки данных уникальны, то для n точек данных будет n-1 точек разбиения. То есть в зависимости от выбранных точки и переменной разбиения мы получаем высокий информационный выигрыш и выбираем разделение с этим выигрышем. В большом наборе данных принято считать только точки разделения при определенных процентах распределения значений: 10, 20, 30%. У нас набор данных небольшой, поэтому, видя все точки разделения данных, я выбрала в качестве точки разделения значения ≤30.

Энтропия чистого подмножества равна нулю. Теперь рассчитаем энтропию другого подмножества. Здесь у нас три голоса за и один против.

Чтобы решить, какой атрибут выбрать для разбиения, нужно вычислить информационный выигрыш.

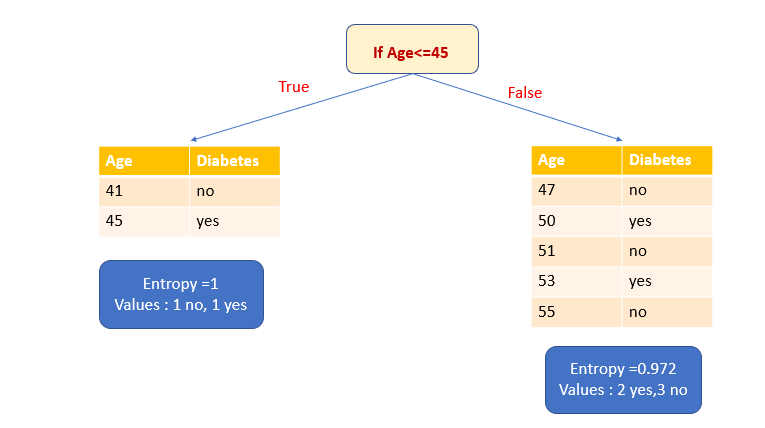
2. Выберем атрибут Age в качестве переменной разбиения и ≤45 в качестве точки разбиения.

Давайте сначала вычислим энтропию подмножества True. У него есть одно да и одно нет. Это высокий уровень неопределенности. Энтропия равна 1. Теперь рассчитаем энтропию подмножества False. В нем два голоса за и три против.

3. Рассчитаем информационный выигрыш.

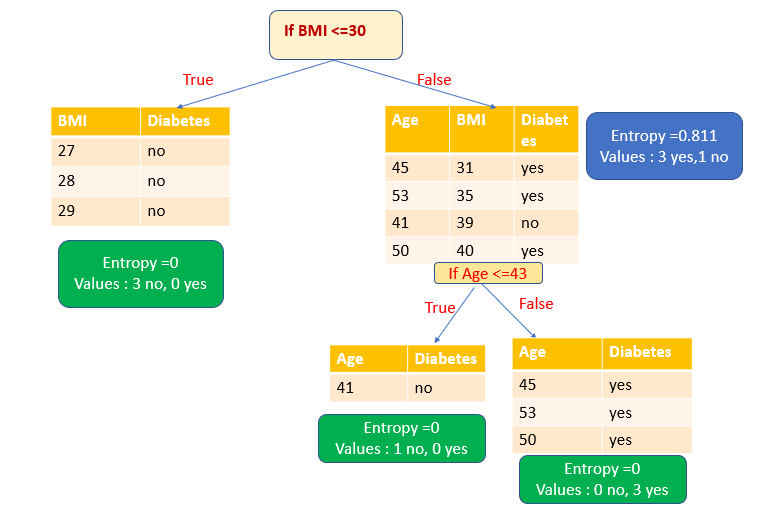
Мы должны выбрать атрибут, имеющий высокий информационный выигрыш. В нашем примере такую ценность имеет только атрибут BMI. Таким образом, атрибут BMI выбирается в качестве переменной разбиения. После разбиения по атрибуту BMI мы получаем одно чистое подмножество (листовой узел) и одно нечистое подмножество. Снова разделим это нечистое подмножество на основе атрибута Age. Теперь у нас есть два чистых подмножества (листовой узел).

Итак, мы создали дерево решений с чистыми подмножествами.

Напишем это на Python с помощью sklearn

1. Импортируем библиотеки.

import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns 

2. Загрузим данные.

df=pd.read_csv("Diabetes1.csv") df.head() 

3. Разделим переменные на x и y.

Атрибуты BMI и Age принимаются за x.
Атрибут Diabetes (целевая переменная) принимается за y.

x=df.iloc[. 2] y=df.iloc[:,2:] x.head(3) 

4. Построим модель с помощью sklearn

from sklearn import tree model=tree.DecisionTreeClassifier(criterion="entropy") model.fit(x,y) 

Вывод: DecisionTreeClassifier (criterion=«entropy»)

5. Оценка модели

Вывод: 1.0 . Мы взяли очень маленький набор данных, поэтому оценка равна 1.

6. Прогнозирование с помощью модели

Давайте предскажем, будет ли диабет у человека 47 лет с ИМТ 29. Напомню, что эти данные есть в нашем наборе данных.

Вывод: array([‘no’], dtype=object)
Прогноз — нет, такой же, как и в наборе данных. Теперь спрогнозируем, будет ли диабет у человека 47 лет с индексом массы тела 45. Отмечу, что этих данных в нашем наборе нет.

Вывод: array([‘yes’], dtype=object)

7. Визуализация модели:

Код и набор данных из этой статьи доступны на GitHub.

Приходите изучать математику к нам на курс «Математика и Machine Learning для Data Science» а промокод HABR, добавит 10 % к скидке на баннере.

Рекомендуемые статьи

Источник