Дерево разметок сети петри

45. Эквивалентность и включение сетей Петри. Построение дерева достижимости сети Петри.

Сети Петри эквивалентны, если они имеют одинаковое множество достижимых состояний или множество реализуемых последовательностей переходов.

Сеть СП1, включается в СП2, если поведение СП1 явл. подмнож. поведения СП2.

Вершинами дерева достижимости явл. разметки сети.

Дерево достижимости представляет все достижимые разметки сети Петри, а также — все возможные последовательности запусков её переходов.

1. Если в дереве есть вершина y, с той же маркировкой (m[x]=m[y]), то х — дублирующая вершина.
2. Если для маркировки m[х] ни один из переходов не разрешен, то х — терминальная.
3. В противном случае, для всякого перехода ti разрешенного в m[х], создаётся новая вершина z дерева достижимости. Маркировка m[z] для позиции pi, определяется по следующим правилам:

1. Если m[х](pi)=w, то m[z](pi)=w.
2. Если на пути от корня к z существует вершина y такая, что все позиции имеют маркировки , чем для вершины z, то маркировка позиции pi, для которых m[z](pi) > m[y](pi), следующая m[z](pi)=w .

1. Строится дуга с меткой ti, направ. от вершины x к вершине z. Вершина х становится внутр., а вершина z — граничной.
2. Алгоритмом останавливается если все вершины дерева станут терминальными, дублирующими.

46. Виды сетей Петри: временная, стохастическая, функциональная, цветная, ингибиторная. Использование сети Петри для проверки абстрактного сценария. Сеть Петри для задачи об обедающих философах.

Временная сеть Петри — переходы обладают весом, опред. продолжит. срабатывания (задержку).

Стохастическая сеть Петри — задержки являются случайными величинами.

Функциональная сеть Петри — задержки определяются как функции аргументов (например, кол-ва меток в позициях, состояния переходов).

Цветная сеть Петри — метки могут быть различных типов, обозначаемых цветами, тип метки может быть использован как аргумент в функциональных сетях.

Ингибиторная сети Петри — возможны ингибиторные дуги, запрещающие срабатывание перехода, если во входной позиции, связанной с переходом ингибиторной дугой находится метка.

Сеть Петри использ. для выявл. ошибок абстрактного сценария системы. С этой целью сценарий трансформир. в сеть Петри и провер. ее св-ва.

Применительно к сценарию проверяются 3 св-ва:

1) Сеть Петри должна быть ограниченной.

2) При работе сети Петри не должны появл. неконечные тупиковые состояния, в которых не активирован ни один переход.

3) При работе сети Петри не должно возникать «ловушек» — циклов без выхода (если объект попал в нее, будет циклич. циркулир., но не сможет выйти).

С еть Петри для задачи об обедающих философах:

Была предложена Дейкстрой.

5 философов гуляют в саду и размышляют. Когда философ чувствует голод, он заходит в столовую, где стоит круглый стол с 5 стульями и миской спагетти посреди стола. На столе — пять вилок, по одной слева и справа от каждого стула. Философ берет 2 вилки и ест спагетти. Утолив голод, философ кладет вилки на стол и выходит в сад размышлять, пока вновь не почувствует голод.

Задача: требуется предложить такую модель, которая позволила бы синхронизировать независимые действия философов и не допускала взаимной блокировки, когда все философы сидят за столом, каждый взял по вилке и никто не может начать есть (состояние тупика).

Пример решения: запрет на присутствие в столовой более 2-х философов (доп. позиция с 2-мя маркерами), запрет на соседство 2-х философов (доп. позиция с 1 маркером).

47. Логическое представление исследуемой системы. Простые и сложные высказывания. Логич. операции. Таблица истинности и таблица Кэли. Конверсия, инверсия, контрапозиция. Необходимое, достаточное, необходимое и достаточное условия.

Логические (формальные) представления системы — описание в виде совокупн. сложных высказ., составл. из простых (элементарных) и логич. связок между ними.

Логич. представ. характеризуются опред. св-вами и набором допустимых преобраз. над ними (операций, правил вывода, …), кот. явл. правильными методами рассуждений — законами логики.

Высказывание — повествовательное предложение , о котором имеет смысл говорить, что оно истинно или ложно.

Простые высказывания рассм. в данном контексте как неделимое целое (аналог эл-та множества).

Сложные высказывания формулируются из простых с помощью логич. связок (операций), заменяющие связки естественного языка в сложных предложениях.

Логическая операция – функция, завис. от логических переменных (= 0,1), кот. может быть = 2 знач: 0 и 1.

Логическая операция — функция вида f(x1,x2,…xn): B n →B, где В — множ., состоящее из 2 эл-тов В=.

В таблице истинности для бинар. операций первые 2 столбца содержат все возмож. наборы операндов, а последующие столбцы — значения логич. функций.

Источник

10.10. Дерево достижимости сети Петри

Основным методом анализа сетей Петри является построение дерева достижимости, позволяющий найти множество маркировок, достижимых из заданной начальной маркировки сети Петри.

Построение дерева достижимости легко выполняется путем счета по компьютерной программе, написанной для данного варианта сети.

Рассмотрим процесс построения дерева достижимости на конкретном примере.

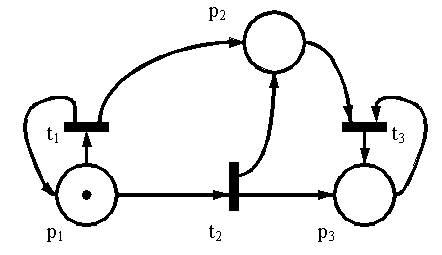
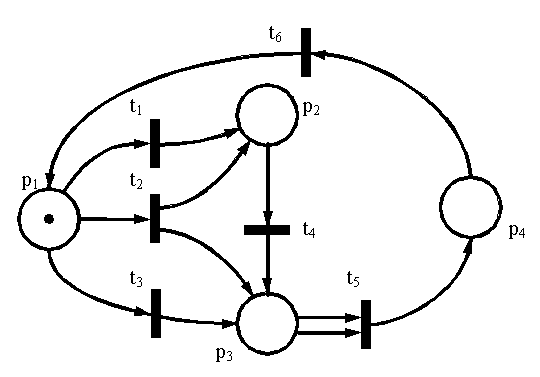
Рис. 10.21. Сеть Петри, для которой строится дерево достижимости.

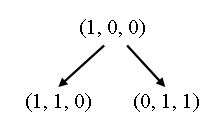
Начальная маркировка сети μ₀ = (1, 0, 0) – фишка находится в позиции p₁. В этот момент разрешены два перехода: t₁ и t₂. Дерево достижимости должно охватывать все возможные варианты эволюции сети. В результате срабатывания перехода t₁ будет достигнута маркировка μ₁ = (1, 1, 0), а в результате срабатывания перехода t₂ — маркировка μ₂ = (0, 1, 1). Фрагмент дерева достижимости для первого шага имеет следующий вид:

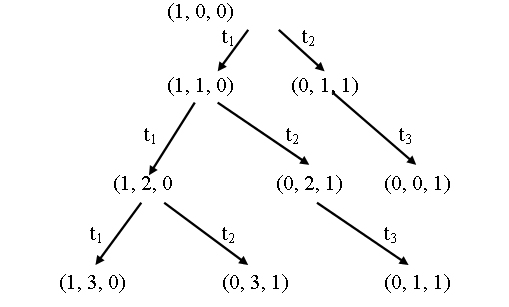
Из маркировки μ₁ = (1, 1, 0) можно запустить переход t₁ и получить маркировку μ₃ = (1, 2, 0).и запустить переход t₂ и получить переход μ₄ = (0, 2, 1). Из маркировки μ₂ = (0, 1, 1) можно запустить переход и получить маркировку μ₅ = (0, 0, 1). В результате получим

дерево достижимости для второго шага построения.

Для третьего шага получим

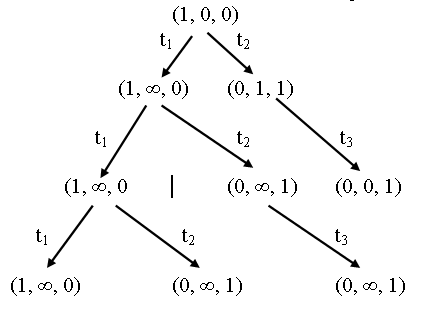
Продолжая таким образом заметим, что в результате для конечной сети Петри строится бесконечное дерево достижимости. Приведение такого дерева к конечному виду проводится следующим способом. Введение новых маркировок ограничивается на каждом шаге граничными вершинами. Это:

• пассивные маркировки, из которых никакие переходы невозможны (такой является маркировка μ₅ = (0, 0, 1), полученная в результате срабатывания переходов t₂ t₃, и
• ранее встречавшиеся маркировки, из которых повторяются уже построенные фрагменты дерева достижимости. Такой является маркировка μ₂ = (0, 1, 1), полученная в результате срабатывания последовательности переходов t₁ t₂ t₃ .

Для этого дерева только маркировка μ₅ = (0, 0, 1) является пассивной. Для всех остальных маркировок некоторые переходы сети оказываются разрешенными, что приводит к постепенному накоплению фишек в позиции p₂. Это означает, что сеть имеет бесконечное множество маркировок, что отмечено на конечном дереве достижимости для этой сети.

Если последовательность маркировок ограничена (символ ∞ отсутствует в дереве достижимости), то число состояний сети Петри конечно. Дерево достижимости является графом состояний для этой сети. В этом практически важном случае находить множество всех достижимых маркировок (множество состояний сети) можно простым перебором. Понятно, что только ограниченная сеть Петри является безопасной, в которой число фишек в позициях не может превышать некоторое конечное число. Такая сеть аппаратно осуществима. Пример ограниченной сети Петри приведен на следующем рисунке.

Рис. 10.22. Ограниченная сеть Петри

Дерево достижимости для этой сети имеет следующий вид:

Граф достижимости показывает, что сеть Петри ограничена и безопасна. Дерево достижимости позволяет легко проверить, является ли сеть сохраняющей или нет. Для этого достаточно сложить количество фишек для каждой маркировки (для каждой вершины дерева достижимости) и сравнить суммы. Если они одинаковы, то сеть сохраняющая. Сеть на рис. 10.22 не является сохраняющей.

Анализ дерева достижимости для ограниченной сети Петри позволяет определить все его свойства, перечисленные выше. Если сеть неограниченна (в разметке дерева достижимости присутствует символ ∞), то анализ сети затруднен. Наличие символа ∞ означает потерю части информации о свойствах сети.

Основным недостатком сетей Петри являются трудности моделирования времени работы (времени задержки) переходов. Поэтому классические сети Петри позволяют эффективно моделировать логику работы программ и технических устройств, но имитационное моделирование временных характеристик в них затруднено. Поэтому разработаны различные варианты расширения возможностей сетей Петри, приспособленных к решению различных конкретных задач.

10.11. Е – сеть

Наиболее современным и продвинутым к задачам графического программирования и моделирования вычислительных систем являются Е–сети (от английского evaluation – вычисления).

Е-сети включают несколько типов позиций:

Меткам (фишкам) в Е-сети могут присваиваться атрибуты.

Переходам приписывается время задержки и функции преобразования атрибутов меток.

Источник

4 Анализ сетей Петри с использованием дерева достижимости и матричных уравнений.

Дерево достижимости: Анализ безопасности и ограниченности . Сеть Петри ограниченна тогда и только тогда, когда символ w отсутствует в ее дереве достижимости. Присутствие символа w в дереве достижимости ( [х](p)=w для некоторой вершины x и позиции p) означает, что для произвольного положительного целого k существует достижимая маркировка со значением в позиции p, большим, чем k (а также бесконечность множества достижимых маркировок). Это, в свою очередь, означает неограниченность позиции p, а следовательно, и самой сети Петри. Отсутствие символа w в дереве достижимости означает, что множество достижимых маркировок конечно. Следовательно, простым перебором можно найти верхнюю границу, как для каждой позиции в отдельности, так и общую верхнюю границу для всех позиций. Последнее означает ограниченность сети Петри. Если граница для всех позиций равна 1, то сеть Петри безопасна. Анализ сохранения. Так как дерево достижимости конечно, для каждой маркировки можно вычислить сумму начальной маркировки. Если эта сумма одинакова для каждой достижимой маркировки, то сеть Петри является сохраняющей. Если суммы не равны, сеть не является сохраняющей. Если маркировка некоторой позиции совпадает с w, то эта позиция должна быть исключена из рассмотрения. Анализ покрываемости. Задача покрываемости: требуется для заданной маркировки ‘ определить, достижима ли маркировка ‘‘ ‘’. Такая задача решается перебором вершин дерева достижимости. При этом ищется такая вершина х, что [x] ‘. Если такой вершины не существует, то маркировка ‘ не

является покрываемой. Если она найдена, то [x] определяет покрывающую маркировку для ‘ Если компонента маркировки [x], соответствующая некоторой позиции p совпадает с w, то конкретное еѐ значение может быть вычислено. В этом случае на пути от начальной маркировки к покрывающей маркировке имеется повторяющаяся последовательность переходов, запуск которой увеличивает значение маркировки в позиции p. Число таких повторений должно быть таким, чтобы значение маркировки в позиции p превзошло или сравнялось с ‘(p). Анализ живости. Переход t сети Петри является потенциально живым, тогда и только тогда, когда он метит некоторую дугу в дереве достижимости этой сети. Ограниченность метода дерева достижимости. Как видно из предыдущего, дерево достижимости можно использовать для решения задач безопасности, ограниченности, сохранения и покрываемости. К сожалению, в общем случае его нельзя использовать для решения задач достижимости и активности, эквивалентности. Решение этих задач ограничено существованием символа w. Символ w означает потерю информации: конкретные количества фишек отбрасываются, учитывается только существование их большого числа. Матричные уравнения. Другой подход к анализу сетей Петри основан на матричном представлении сетей Петри и решении матричных уравнений. Альтернативным по отношению к определению сети Петри N в виде (P,T,I,O) является определение сети N в виде двух матриц D — и D + , представляющих входную и выходную функции I и O. Пусть каждая из матриц D — и D + имеет m=|T| строк (по одной на

переход) и n=|P| столбцов (по одному на позицию).
Матричный вид сети Петри N=(P,T,I,O) задаѐтся парой ( D -, D +), где
D -[k,i] = ^ #(pi,tk) – кратность дуги, ведущей из позиции pi в переход tk.
D +[k,i] = # ^ (pi,tk) – кратность дуги, ведущей из перехода tk в позицию pi,
для произвольных 1 k m, 1 i n.
Пусть e[k] — m-вектор, k-тый элемент которого равен 1, а остальные равны 0. Переход tk, 1 k		m,
в маркировке	разрешен, если > e[k]× D -. Результатом запуска разрешѐнного перехода tk	в
маркировке	является следующая ниже маркировка ‘:

‘= — e[k]× D — + e[k]× D +== + e[k]× D , где D =( D + — D -) — составная матрица изменений .

Источник