Дерево решений экономический анализ

31.7. «Дерево» решений

Примеры, которые мы рассматривали до сих пор, включа­ли получение единого решения. Однако на практике результат одного решения приводит к необходимости принятия следую­щего решения и т.д. Эту последовательность принятия реше­ний нельзя выразить таблицей доходов, поэтому приходится использовать другой алгоритм принятия управленческих ре­шений.

Графически подобные процессы могут быть представлены с помощью «дерева» решений. Такое представление облегчает описание многоэтапного процесса принятия управленческого решения в целом.

Рассмотрим «дерево» решений, которое применяют тогда, когда нужно принять несколько взаимосвязанных решений в условиях неопределенности в случае принятия решения, зави­сящего от исхода предыдущего или исходов испытаний.

Составляя дерево решений, рисуют «ствол» и «ветви», ото­бражающие структуру проблемы. Располагают «дерево» ре­шений слева направо. «Ветви» обозначают возможные альтер­нативные решения, которые могут быть приняты, и возмож­ные исходы, возникающие в результате этих решений.

Квадратные «узлы» на дереве решений обозначают места, в которых принимаются решения, круглые «узлы» — места исходов. Так как не представляется возможным влиять на по­явление исходов, то в круглых узлах вычисляют вероятнос­ти их появления. Когда все решения и их исходы указаны на «дереве», оценивается каждый из вариантов и проставляются денежные доходы. Все расходы, вызванные решениями, про­ставляются на соответствующих «ветвях».

Рассмотрим задачу с применением «дерева» решений.

Выбор оптимальной стратегии развития предприятия в условиях трансформации рынка

Фирма может принять решение о строительстве средне­го или малого предприятия. Малое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать на сооружае­мом предприятии. Строительство среднего предприятия эко­номически оправданно при высоком спросе. С другой стороны, можно построить малое предприятие и через два года его рас­ширить.

Фирма рассматривает данную задачу на десятилетний пе­риод. Анализ рыночной ситуации показывает, что вероятности высокого и низкого уровней спроса равны 0,7 и 0,3 соот­ветственно. Строительство среднего предприятия обойдется в 4 млн р., малого — в 1 млн р. Затраты на расширение через два года малого предприятия оцениваются в 3,5 млн р.

Ожидаемые ежегодные доходы для каждой из возможных альтернатив:

• среднее предприятие при высоком (низком) спросе дает 0,9 (0,2) млн р.;
• малое предприятие при низком спросе дает 0,1 млн р.;
• малое предприятие при высоком спросе дает 0,2 млн р. в течение 10 лет;
• расширенное предприятие при высоком (низком) спросе дает 0,8 (0,1) млн р.;
• малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает 0,1 млн р. в год за остальные восемь лет.

Определить оптимальную стратегию фирмы в строительстве предприятий. Решение. Данная задача является многоэтапной, так как если фирма решит строить малое предприятие, то через два года она может принять решение о его расширении. В этом случае процесс принятия решения состоит из двух этапов: ре­шение в настоящий момент времени о размере предприятия и решение о необходимости его расширения, принимаемое через два года. На рис. 31.7 задача представлена в виде «дерева» решений. Предполагается, что спрос может оказаться высоким и низ­ким. Дерево имеет два типа вершин: «решающие» вершины, обозначенные квадратными узлами, и «случайные» вершины, обозначенные круглыми узлами. 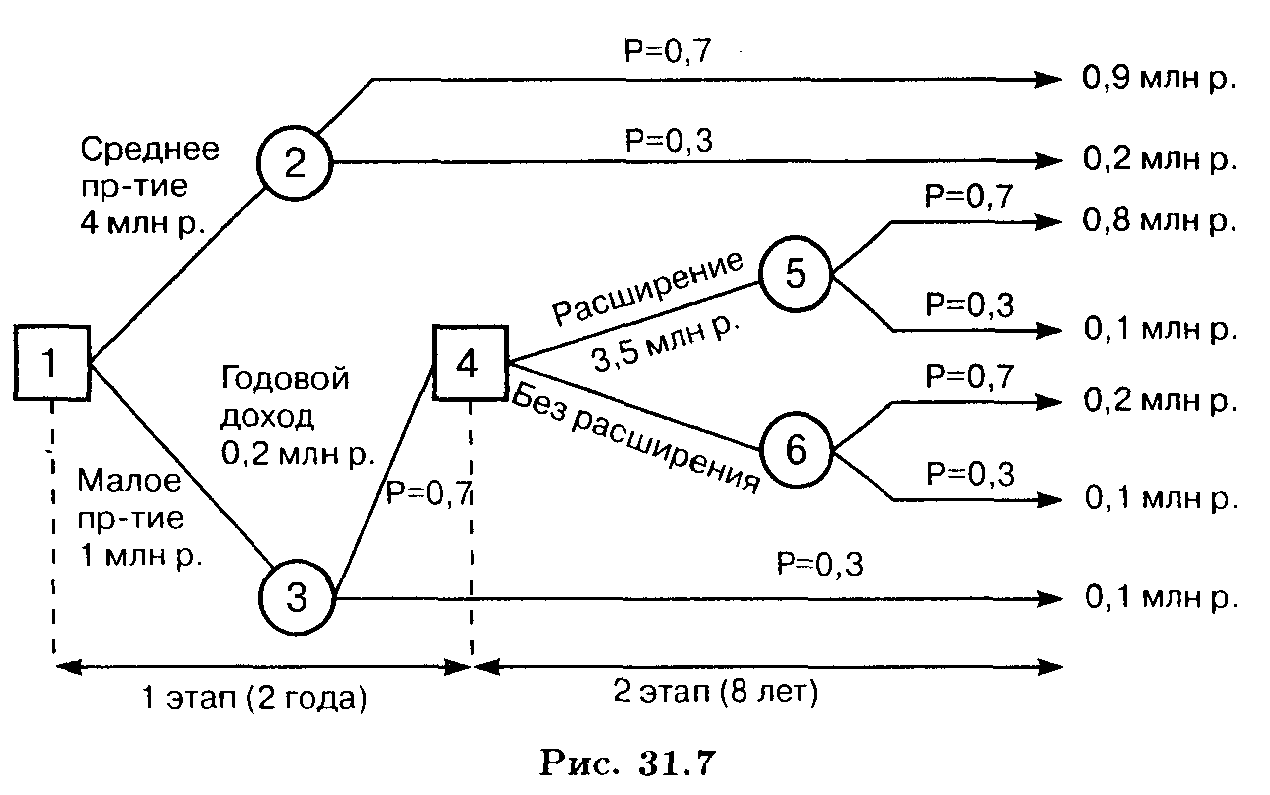Начиная с вершины 1, являющейся «решающей», необходи­мо принять решение относительно размера предприятия. Вер­шины 2 и 3 являются «случайными». Фирма будет рассматри­вать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет устано­вится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или нерасширении предприятия. Вершины 5 и 6 будут «случайными». Произведем расчеты для каждой из альтернатив. Вычис­ления начнем со 2-го этапа. Для последних восьми лет альтер­нативы, относящиеся к вершине 4, оцениваются так: где ДР — доход с расширением, ДБР — доход без расширения предприятия. Таким образом, в вершине 4 выгоднее не проводить расши­рение, при этом доход составит l,36 млн р. Теперь для дальнейших расчетов оставим одну «ветвь», выходящую из вершины 4, которой соответствует доход 1,36 млн р. за остальные восемь лет. Перейдем к вычислениям 1-го этапа. Для вершины 1 где ДС — доход среднего предприятия, ДМ — доход малого предприятия. Сравнивая получаемые в вершине 1 доходы среднего и ма­лого предприятий, видим, что более предпочтительным явля­ется вариант строительства среднего предприятия. Таким образом, фирме целесообразно построить среднее предприятие.

Источник

Метод «дерево решений»

Для анализа рисков инновационных проектов часто применяют метод дерева решений. Он предполагает, что у проекта существует несколько вариантов развития. Каждое решение, принимаемое по проекту, определяет один из сценариев его дальнейшего развития. При помощи дерева решений решаются задачи классификации и прогнозирования. Дерево решений – это схематическое представление проблемы принятия решений. Ветви дерева решений представляют собой различные события (решения), а его вершины – ключевые состояния, в которых возникает необходимость выбора. Чаще всего дерево решений является нисходящим, т. е. строится сверху вниз.

Выделяют следующие этапы построения дерева решений:

1. Первоначально обозначают ключевую проблему. Это будет вершина дерева.

2. Для каждого момента определяют все возможные варианты дальнейших событий, которые могут оказать влияние на ключевую проблему. Это будут исходящие от вершины дуги дерева.

3. Обозначают время наступления событий.

4. Каждой дуге прописывают денежную и вероятностную характеристики.

5. Проводят анализ полученных результатов.

Основа наиболее простой структуры дерева решений – ответы на вопросы «да» и «нет».

Пример 1. Рассмотрим пример дерева решений, задача которого – ответить на вопрос «Пойти ли гулять?». Чтобы решить эту задачу, необходимо ответить на ряд вопросов, которые находятся в узлах дерева (рис. 8.1). Вершина дерева «На улице солнечно» является узлом проверки. Если на этот вопрос получен положительный ответ, то переходим к левой ветви дерева, если отрицательный – то к правой. Движение продолжается до тех пор, пока не будет получен окончательный ответ.

Рис. 8.1. Дерево решений «пойти ли гулять»

Для каждой дуги дерева могут быть определены числовые характеристики, например величина прибыли по проекту и вероятность ее получения. В этом случае оно помогает учесть все возможные варианты действия и соотнести с ними финансовые результаты. Для формулирования сценариев развития проекта необходимо располагать достоверной информацией с учетом вероятности и времени наступления событий. Затем переходят к сравнению альтернатив.

Пример 2. Компания «Конфетти» в настоящее время выпускает плитки молочного шоколада. Директор по развитию считает, что на рынке повысился спрос на молочный шоколад с наполнителями. Перед компанией стоит вопрос: переходить ли на производство молочного шоколада с наполнителем или не стоит этого делать? Если производить шоколад обоих типов, то потребуется увеличить производственные мощности. Информация об ожидаемых выигрышах и вероятности событий в случае того или иного решения представлена на дереве решений (рис. 8.2). Используя дерево решений, руководитель находит наиболее предпочтительное решение – увеличить производственные мощности. Это обусловлено ожидаемой прибылью – 2 млн руб., которая превышает прибыль 1 млн руб. при отказе от такого наращивания, если в точке «а» будет низкий спрос. Руководитель, двигаясь к первой точке принятия решения, рассчитывает предполагаемую прибыль в случае альтернативных действий.

Рис. 8.2. Дерево решений «какой шоколад производить»

Для производства только молочного шоколада с наполнителем она составит 4,4 млн руб. (5 × 0,8 + 0,2 × 2). Аналогично рассчитывается ожидаемое значение для варианта выпуска только молочного шоколада без наполнителя, которое равно всего 2,55.

Таким образом, наращивание производственных мощностей является наиболее желательным решением и приносит наибольший выигрыш.

Пример 3. Руководителю отдела нужно принять решение относительно закупки станков. Второй станок более экономичный, но и в то же время более дорогой и требует больших накладных расходов (рис. 8.3). Руководителю нужно выбрать тот станок, который обеспечит максимизацию прибыли.

Оборудование	Постоянные расходы	Операционный расход на единицу техники
Станок 1	500 000
Станок 2	700 000

Рис. 8.3. Дерево решений

Руководитель оценивает вероятность спроса на продукцию, производимую на станках:

· 2 000 ед. с вероятностью 0,4;

· 3 000 ед. с вероятностью 0,6.

Станок 1: 840 000 × 0,4 + 1 510 000 × 0,6 = 1 242 000.

Станок 2: 1 180 000 × 0,4 + 2 120 000 × 0,6 = 1 744 000.

Таким образом, приобретение второго станка более экономично.

Недостатками дерева решений является ограниченное число вариантов решения проблемы. В процессе построения дерева решений необходимо обращать внимание на его размер. Оно не должно быть слишком перегруженным, т. к. это уменьшает способность к обобщению и способность давать верные ответы.

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:

Источник