3.3 Дерево решений
Таблицу решений удобно использовать при анализе задач, имеющих одно множество альтернативных решений и одно множество состояний среды. Многие задачи требуют анализа последовательности решений и состояний среды, когда одна совокупность стратегий игрока и состояний природы порождает другое состояние подобного типа. Если имеют место два или более последовательных множества решений, причем последующие решения основываются на результатах предыдущих, и/или два или более множества состояний среды (т.е. появляется целая цепочка решений, вытекающих одно из другого, которые соответствуют событиям, происходящим с некоторой вероятностью), используется дерево решений.
Дерево решений – это графическое изображение процесса решений, в котором отражены альтернативные решения, состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.
Процесс принятия решения с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.
Этап 1. Формулировка задачи. Прежде всего, необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к поддающейся анализу форме. Должны быть выполнены следующие основные процедуры: определение возможностей сбора информации для экспериментирования и реальных действий; составление перечня событий, которые с определенной вероятностью могут произойти; установление временного порядка расположения событий, в исходах которых содержится полезная и доступна информация, и тех последовательных действий, которые можно предпринять.
Этап 2. Построение дерева решений
Этап 3. Оценка вероятностей состояний среды, т.е. сопоставление шансов возникновения каждого конкретного события. Следует отметить, что указанные вероятности определяются либо н основании имеющейся статистики, либо экспертным путем.
Этап 4. Установление выигрышей (или проигрышей, как выигрышей со знаком минус) для каждой возможной комбинации альтернатив (действий) и состояний среды.
Этап 5. Решение задачи путем расчета ожидаемой стоимостной ценности (EMV) для каждой вершины состояния среды.
Дерево решений для компании «Буренка» изображено на следующей схеме.
EMV для вершины 1 = (0,5)(200)+(0,5)(-180) = 10
EMV для вершины 2 = (0,5)(100)+(0,5)(-20) = 40
3.4 Ожидаемая ценность достоверной информации
Предположим, что менеджер компании «Буренка» связался с фирмой, занимающейся исследованием рынка, которая предложила ему помочь в принятии решений о том, стоит ли создавать производство навесов для хранение кормов. Исследователи рынка утверждают, что их анализ позволит установить с полной определенностью, будет ли рынок благоприятным для данного продукта. Другими словами, условия в компании меняются в зависимости от того, принимается ли решение в условиях риска или же в условиях определенности. Эта информация может предостеречь Бычкова от очень дорогостоящей ошибки. Фирма, занимающаяся исследованием рынка, хотела бы получить за эту информацию 65 тыс. руб. Чтобы Вы порекомендовали Бычкову? Следует ли заказать проведение исследования рынка? Даже если результаты этого исследования являются совершенно точными, оправдана ли плата в 65 тыс. руб.?
Ожидаемой ценностью достоверной информацией (EVPI) назовем разность между выигрышем в условиях определенности и выигрышем в условиях риска:
EVPI = ожидаемый выигрыш в условиях определенности – максимум EMV
Для того, чтобы определить EVPI, мы должны вначале рассчитать математическое ожидание EMV в условиях определенности, которое равно ожидаемому, или среднему, доходу в случае, когда мы имеем достоверную информацию перед тем, как принять решение.
- Лучший исход для состояния среды «благоприятный рынок» – «создать большое производство» с выигрышем 200 тыс. руб. Лучший исход для состояния среды «неблагоприятный рынок» – «ничего не делать» с выигрышем 0. Ожидаемая ценность в условиях определенности = (200)(0,5) + (0)(0,5)=100. Итак, если бы мы располагали достоверной информацией, то ожидали бы получить в среднем 100 тыс. руб.
- Максимум EMV = 40 — ожидаемый доход без достоверной информации.
- EVPI = ценность в условиях определенности — максимум EMV = 100 — 40 = 60.
Итак, Бычкову следовало бы платить за достоверную информацию не более 60 тыс. руб. Конечно, такой вывод основывается на предположении, что вероятность реализации каждого состояния среды равна 0,5.
Предположим, что Бычкову надо принять два решения, причем второе решение зависит от исхода первого. Прежде чем создать новое производство, Бычков имеет намерение заказать исследование рынка и заплатить за него 10 тыс. руб. Результаты этого исследования могли бы помочь решить вопрос о том, следует ли создавать большое производство, малое производство или не делать ничего. Бычков понимает, что такое обследование рынка не может дать достоверную информацию, но может, тем не менее, оказаться полезным.
На рис. 3.1 показаны возможные состояния среды и решения, а также вероятности различных результатов обследования вероятности наступления различных состояний среды.
Дерево решений имеет два типа вершин:
Дерево решений Бычкова с рассчитанными EMV представлена на следующем рис. 3.2. Короткими параллельными линиями отсекается та ветвь, которая оказывается менее благоприятной по сравнению с другими и может быть отброшена.
Ожидаемая ценность наилучшего решения в случае, если будет заказано обследование рынка, составляет 49,2 тыс. руб. Ожидаемая ценность наилучшего решения без обследования составляет 40 тыс. руб.
Пример 3.2 Компания «Молодой сыр» — небольшой производитель различных продуктов из сыра. Один из продуктов — сырная паста — продается в розницу. Вадим Ароматов, менеджер компании должен решить, сколько ящиков сырной пасты следует производить в течение месяца. Вероятности того, что спрос на сырную пасту будет 6, 7, 8 или 9 ящиков равны соответственно 0,1; 0,3; 0,5; 0,1. Затраты на производство одного ящика 45 руб. Ароматов продает каждый ящик по цене 95 руб. Если ящик сырной пасты не продается в течение месяца, то она портится и компания не получает дохода.
- Сколько ящиков следует производить в течение месяца?
- Какова ожидаемая стоимостная ценность этого решения?
Пользуясь исходными данными, построим матрицу игры. Стратегиями игрока 1 (компания «Российский сыр») являются различные показатели числа ящиков с сырной пастой, которые ему, возможно, следует производить. Состояниями природы выступают величины спроса на аналогичное число ящиков.
Вычислим, например, показатель прибыли, которую получит производитель, если он произведет 8 ящиков, а спрос будет только на 7.
Каждый ящик продается по 95 руб. Компания продала 7, а произвела 8 ящиков. Следовательно, выручка будет , а издержки производства 8 ящиков . Итого прибыль от указанного сочетания спроса и предложения будет равна: руб. Аналогично производятся расчеты при других сочетаниях спроса и предложения.
В итоге получим следующую платежную матрицу. Как видно из таблицы, наибольшая средняя ожидаемая прибыль равна 352,5 руб. Она отвечает производству 8 ящиков.
Источник
Дерево решений
Пример №1 . Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.
Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: «решающие» и «случайные» (рис.).
Рис. Дерево решений
Начиная с «решающей» вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 «случайные».
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.
Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в «решающих» вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ = (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ – доход от частичной замены оборудования на более совершенное; ДДР – доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ > ДДР , то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для «решающей» вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН – доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН > ДЗО , то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.
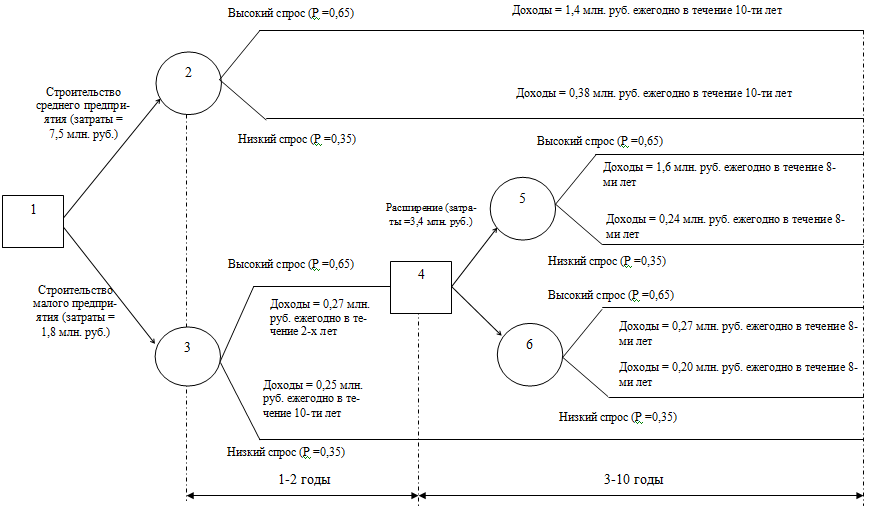
- среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
- малое предприятие при низком спросе – L=0,25 млн. руб.;
- малое предприятие при высоком спросе – М=0,27 млн. руб.;
- расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
- малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.
Начиная с вершины 1, являющейся «решающей», необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или не расширении предприятия. Вершины 5 и 6 будут «случайными».
Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:
— доход малого предприятия с последующим расширением:
ДР = (1,6*0,65 + 0,24*0,35)*8 – 3,4 = 5,592 млн. руб.
— доход малого предприятия без расширения
ДБР = (0,27*0,65 + 0,2*0,35)*8 = 1,964 млн. руб.
Таким образом, в вершине 4 выгоднее провести расширение, при этом доход составит 5,592 млн. руб.
Перейдем к вычислениям 1-го этапа. Для вершины 1:
— доход среднего предприятия:
ДС = (1,4*0,65 + 0,38*0,35)*10 – 7,5 = 2,93 млн. руб.
— доход малого предприятия с последующим расширением через 2 года:
ДМ = 5,592 + 0,27*0,65*2 + 0,25*0,35*10 – 1,8 = 5,018 млн. руб.
Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства малого предприятия с последующим расширением через 2 года.
Источник