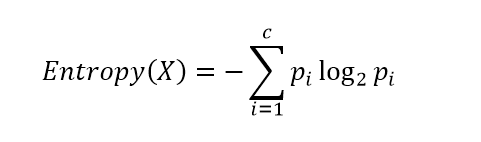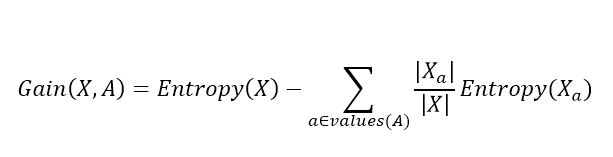Методы классификации и прогнозирования. Деревья решений
Аннотация: Описывается метод деревьев решений. Рассматриваются элементы дерева решения, процесс его построения. Приведены примеры деревьев, решающих задачу классификации. Даны алгоритмы конструирования деревьев решений CART и C4.5.
Метод деревьев решений ( decision trees ) является одним из наиболее популярных методов решения задач классификации и прогнозирования. Иногда этот метод Data Mining также называют деревьями решающих правил , деревьями классификации и регрессии.
Как видно из последнего названия, при помощи данного метода решаются задачи классификации и прогнозирования.
Если зависимая, т.е. целевая переменная принимает дискретные значения, при помощи метода дерева решений решается задача классификации.
Если же зависимая переменная принимает непрерывные значения, то дерево решений устанавливает зависимость этой переменной от независимых переменных, т.е. решает задачу численного прогнозирования.
Впервые деревья решений были предложены Ховилендом и Хантом (Hoveland, Hunt) в конце 50-х годов прошлого века. Самая ранняя и известная работа Ханта и др., в которой излагается суть деревьев решений — «Эксперименты в индукции» («Experiments in Induction «) — была опубликована в 1966 году.
В наиболее простом виде дерево решений — это способ представления правил в иерархической, последовательной структуре. Основа такой структуры — ответы «Да» или «Нет» на ряд вопросов.
На рис. 9.1 приведен пример дерева решений, задача которого — ответить на вопрос: «Играть ли в гольф?» Чтобы решить задачу, т.е. принять решение, играть ли в гольф, следует отнести текущую ситуацию к одному из известных классов (в данном случае — «играть» или «не играть»). Для этого требуется ответить на ряд вопросов, которые находятся в узлах этого дерева, начиная с его корня.
Первый узел нашего дерева «Солнечно?» является узлом проверки , т.е. условием. При положительном ответе на вопрос осуществляется переход к левой части дерева, называемой левой ветвью , при отрицательном — к правой части дерева. Таким образом, внутренний узел дерева является узлом проверки определенного условия. Далее идет следующий вопрос и т.д., пока не будет достигнут конечный узел дерева, являющийся узлом решения . Для нашего дерева существует два типа конечного узла : «играть» и «не играть» в гольф.
В результате прохождения от корня дерева (иногда называемого корневой вершиной) до его вершины решается задача классификации, т.е. выбирается один из классов — «играть» и «не играть» в гольф.
Целью построения дерева решения в нашем случае является определение значения категориальной зависимой переменной.
Итак, для нашей задачи основными элементами дерева решений являются:
Внутренний узел дерева или узел проверки : «Температура воздуха высокая?», «Идет ли дождь?»
Лист , конечный узел дерева, узел решения или вершина : «Играть», «Не играть»
Ветвь дерева (случаи ответа): «Да», «Нет».
В рассмотренном примере решается задача бинарной классификации , т.е. создается дихотомическая классификационная модель. Пример демонстрирует работу так называемых бинарных деревьев.
В узлах бинарных деревьев ветвление может вестись только в двух направлениях, т.е. существует возможность только двух ответов на поставленный вопрос («да» и «нет»).
Бинарные деревья являются самым простым, частным случаем деревьев решений. В остальных случаях, ответов и, соответственно, ветвей дерева, выходящих из его внутреннего узла , может быть больше двух.
Рассмотрим более сложный пример. База данных , на основе которой должно осуществляться прогнозирование, содержит следующие ретроспективные данные о клиентах банка, являющиеся ее атрибутами: возраст, наличие недвижимости, образование, среднемесячный доход, вернул ли клиент вовремя кредит . Задача состоит в том, чтобы на основании перечисленных выше данных (кроме последнего атрибута) определить, стоит ли выдавать кредит новому клиенту.
Как мы уже рассматривали в лекции, посвященной задаче классификации, такая задача решается в два этапа: построение классификационной модели и ее использование.
На этапе построения модели, собственно, и строится дерево классификации или создается набор неких правил . На этапе использования модели построенное дерево , или путь от его корня к одной из вершин, являющийся набором правил для конкретного клиента, используется для ответа на поставленный вопрос «Выдавать ли кредит ?»
Правилом является логическая конструкция, представленная в виде «если : то :».
На рис. 9.2. приведен пример дерева классификации, с помощью которого решается задача «Выдавать ли кредит клиенту?». Она является типичной задачей классификации, и при помощи деревьев решений получают достаточно хорошие варианты ее решения.
Как мы видим, внутренние узлы дерева (возраст, наличие недвижимости, доход и образование) являются атрибутами описанной выше базы данных . Эти атрибуты называют прогнозирующими, или атрибутами расщепления (splitting attribute ). Конечные узлы дерева, или листы, именуются метками класса, являющимися значениями зависимой категориальной переменной «выдавать» или «не выдавать» кредит .
Каждая ветвь дерева, идущая от внутреннего узла , отмечена предикатом расщепления . Последний может относиться лишь к одному атрибуту расщепления данного узла. Характерная особенность предикатов расщепления : каждая запись использует уникальный путь от корня дерева только к одному узлу-решению. Объединенная информация об атрибутах расщепления и предикатах расщепления в узле называется критерием расщепления (splitting criterion ) [33].
На рис. 9.2. изображено одно из возможных деревьев решений для рассматриваемой базы данных . Например, критерий расщепления «Какое образование?», мог бы иметь два предиката расщепления и выглядеть иначе: образование «высшее» и «не высшее». Тогда дерево решений имело бы другой вид.
Таким образом, для данной задачи (как и для любой другой) может быть построено множество деревьев решений различного качества, с различной прогнозирующей точностью.
Качество построенного дерева решения весьма зависит от правильного выбора критерия расщепления . Над разработкой и усовершенствованием критериев работают многие исследователи.
Метод деревьев решений часто называют «наивным» подходом [34]. Но благодаря целому ряду преимуществ, данный метод является одним из наиболее популярных для решения задач классификации.
Источник
Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
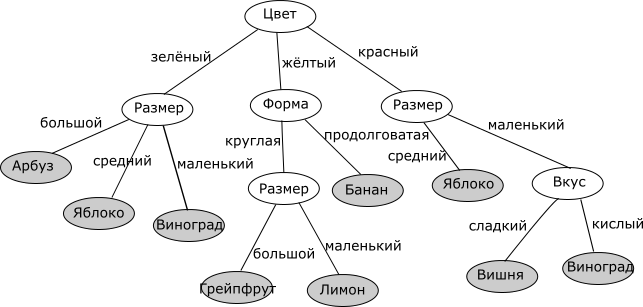
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник