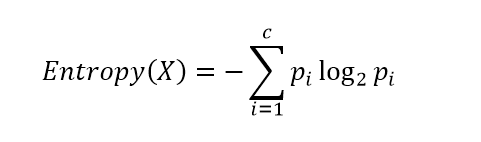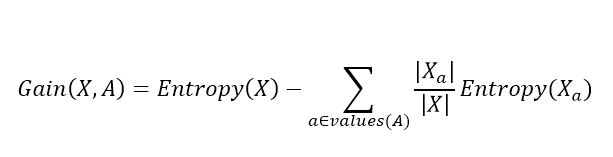Дерево решений
Деревья решений – популярный алгоритм классификации, в котором решающие правила извлекаются непосредственно из исходных данных в процессе обучения. Они представляют собой иерархическую последовательность правил вида «Если…то…».
Деревья решений способны выявить нелинейные зависимости и нетипичные (редкие) случаи. Данный алгоритм обработки подробно рассмотрен в статье «Деревья решений — общие принципы работы».
Примеры применения
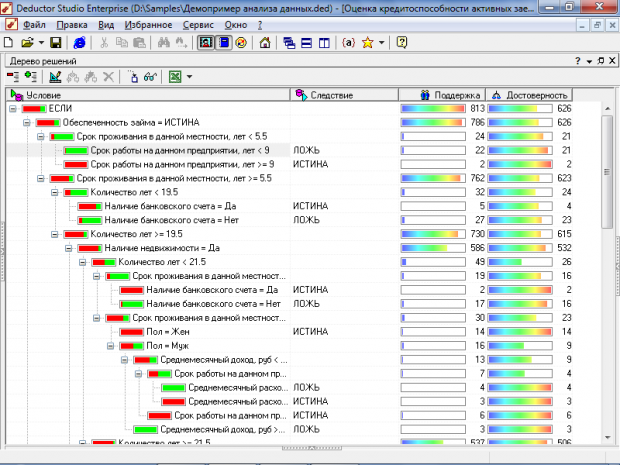
Оценка кредитоспособности клиента при выдаче кредитов. На базе алгоритма строятся скоринговые карты, модели аппликационного и поведенческого скоринга. Это позволяет проводить выбранную кредитную политику и снижать уровень просроченной задолженности.
Контроль за качеством продукции в промышленности. Алгоритм позволяет автоматически выявлять отклонение от заданных параметров, выявлять дефекты, проводить испытания без разрушения (например, проверка качества сварки).
Диагностика различных заболеваний. Обеспечение поддержки принимаемых врачом решений для повышения эффективности постановки диагноза.
Управление проектами. Алгоритм позволяет рассматривать альтернативные последствия принятия решения и последствия их выбора с учетом проектных рисков. Анализ ожидаемого денежного значения с целью определения относительной стоимости альтернативных действий.
Описание алгоритма
Для принятия решения, к какому классу следует отнести некоторый объект или ситуацию, требуется ответить на вопросы, стоящие в узлах этого дерева, начиная с его корня. Вопросы имеют вид, например «значение параметра А больше В?». Если ответ положительный, осуществляется переход к правому узлу следующего уровня. Затем снова идет вопрос, связанный с соответствующим узлом и т. д.
Для интерпретации результатов классификации с помощью дерева решений используются визуализаторы, показывающие структуру дерева, а также сформулированные в нем правила.
В Deductor Studio подобный класс задач реализуется посредством наиболее популярного алгоритма C4.5., в котором количество потомков у узла не ограничено. Не умеет работать с непрерывным целевым полем, поэтому решает только задачи классификации.
Источник
Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
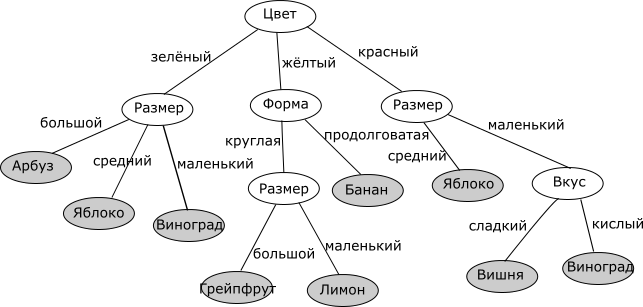
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник