8.10. Метод «дерево решений»
Для анализа рисков инновационных проектов часто применяют метод дерева решений. Он предполагает, что у проекта существует несколько вариантов развития. Каждое решение, принимаемое по проекту, определяет один из сценариев его дальнейшего развития. При помощи дерева решений решаются задачи классификации и прогнозирования. Дерево решений – это схематическое представление проблемы принятия решений. Ветви дерева решений представляют собой различные события (решения), а его вершины – ключевые состояния, в которых возникает необходимость выбора. Чаще всего дерево решений является нисходящим, т. е. строится сверху вниз. Выделяют следующие этапы построения дерева решений:
- Первоначально обозначают ключевую проблему. Это будет вершина дерева.
- Для каждого момента определяют все возможные варианты дальнейших событий, которые могут оказать влияние на ключевую проблему. Это будут исходящие от вершины дуги дерева.
- Обозначают время наступления событий.
- Каждой дуге прописывают денежную и вероятностную характеристики.
- Проводят анализ полученных результатов.
Основа наиболее простой структуры дерева решений – ответы на вопросы «да» и «нет». Пример 1. Рассмотрим пример дерева решений, задача которого – ответить на вопрос «Пойти ли гулять?». Чтобы решить эту задачу, необходимо ответить на ряд вопросов, которые находятся в узлах дерева (рис. 8.1). Вершина дерева «На улице солнечно» является узлом проверки. Если на этот вопрос получен положительный ответ, то переходим к левой ветви дерева, если отрицательный – то к правой. Движение продолжается до тех пор, пока не будет получен окончательный ответ.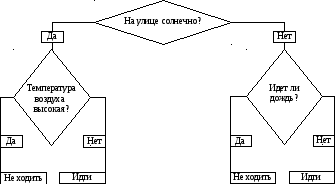 
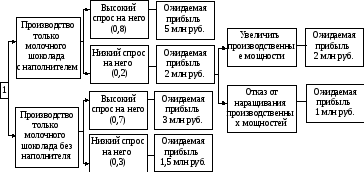
Рис. 8.1. Дерево решений «пойти ли гулять» Для каждой дуги дерева могут быть определены числовые характеристики, например величина прибыли по проекту и вероятность ее получения. В этом случае оно помогает учесть все возможные варианты действия и соотнести с ними финансовые результаты. Для формулирования сценариев развития проекта необходимо располагать достоверной информацией с учетом вероятности и времени наступления событий. Затем переходят к сравнению альтернатив. Пример 2. Компания «Конфетти» в настоящее время выпускает плитки молочного шоколада. Директор по развитию считает, что на рынке повысился спрос на молочный шоколад с наполнителями. Перед компанией стоит вопрос: переходить ли на производство молочного шоколада с наполнителем или не стоит этого делать? Если производить шоколад обоих типов, то потребуется увеличить производственные мощности. Информация об ожидаемых выигрышах и вероятности событий в случае того или иного решения представлена на дереве решений (рис. 8.2). Используя дерево решений, руководитель находит наиболее предпочтительное решение – увеличить производственные мощности. Это обусловлено ожидаемой прибылью – 2 млн руб., которая превышает прибыль 1 млн руб. при отказе от такого наращивания, если в точке «а» будет низкий спрос. Руководитель, двигаясь к первой точке принятия решения, рассчитывает предполагаемую прибыль в случае альтернативных действий. 
Рис. 8.2. Дерево решений «какой шоколад производить» Для производства только молочного шоколада с наполнителем она составит 4,4 млн руб. (5 × 0,8 + 0,2 × 2). Аналогично рассчитывается ожидаемое значение для варианта выпуска только молочного шоколада без наполнителя, которое равно всего 2,55. Таким образом, наращивание производственных мощностей является наиболее желательным решением и приносит наибольший выигрыш. Пример 3. Руководителю отдела нужно принять решение относительно закупки станков. Второй станок более экономичный, но и в то же время более дорогой и требует больших накладных расходов (рис. 8.3). Руководителю нужно выбрать тот станок, который обеспечит максимизацию прибыли.
| Оборудование | Постоянные расходы | Операционный расход на единицу техники |
| Станок 1 | 500 000 | 670 |
| Станок 2 | 700 000 | 940 |
Рис. 8.3. Дерево решений Руководитель оценивает вероятность спроса на продукцию, производимую на станках:
- 2 000 ед. с вероятностью 0,4;
- 3 000 ед. с вероятностью 0,6.
Станок 1: 840 000 × 0,4 + 1 510 000 × 0,6 = 1 242 000. Станок 2: 1 180 000 × 0,4 + 2 120 000 × 0,6 = 1 744 000. Таким образом, приобретение второго станка более экономично. Недостатками дерева решений является ограниченное число вариантов решения проблемы. В процессе построения дерева решений необходимо обращать внимание на его размер. Оно не должно быть слишком перегруженным, т. к. это уменьшает способность к обобщению и способность давать верные ответы.
Источник
1. Дерево решений
Своевременная разработка и принятие правильного решения — главные задачи работы управленческого персонала любой организации. Непродуманное решение может дорого стоить компании. На практике результат одного решения заставляет нас принимать следующее решение и т. д. Когда нужно принять несколько решений в условиях неопределенности, когда каждое решение зависит от исхода предыдущего или исходов испытаний, то применяют схему, называемую деревом решений.
Дерево решений — это графическое изображение процесса принятия решений, в котором отражены альтернативные решения, альтернативные состояния среды, соответствующие вероятности и выигрыши для любых комбинаций альтернатив и состояний среды.
Рисуют деревья слева направо. Места, где принимаются решения, обозначают квадратами □, места появления исходов — кругами О,
возможные решения — пунктирными линиями—-, возможные исходы — сплошными линиями—-.
Задачи с решениями
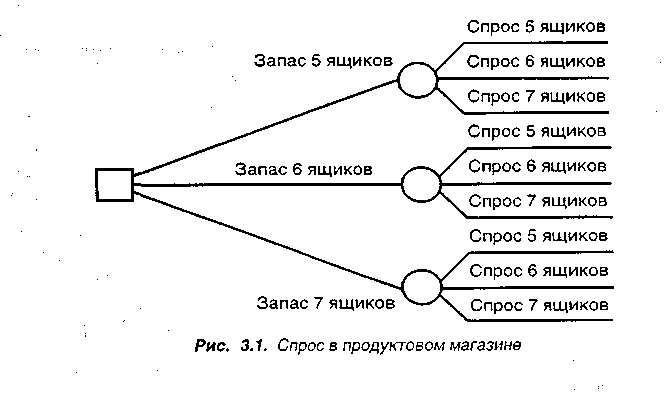
З адача 3.1 Ежедневный спрос на ящики с напитком в продуктовом магазине может быть пять, шесть или семь ящиков. Покажем дерево решений, которое иллюстрирует альтернативы запасов пяти, шести или семи ящиков.
Решение Дерево решений показано на рис. 3.1.
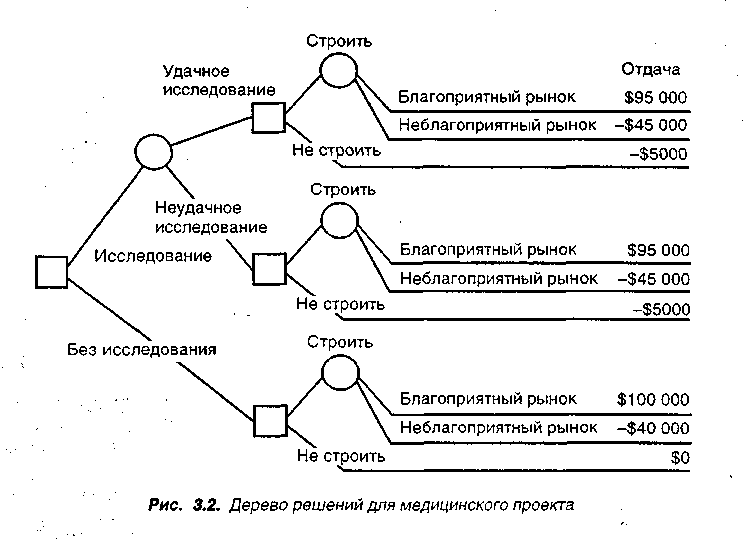
З адача 3.2 Группа медиков собирается открыть частную медицинскую фирму. Если рынок будет благоприятным, они будут иметь прибыль $100000. Если рынок неблагоприятный, они понесут потери $40000. Они также могут осуществить маркетинговое исследование, которое стоит $5000. Результаты исследования могут быть благоприятными или неблагоприятными. Медики хотят построить дерево решений и отразить на нем свою денежную отдачу. Дерево решений показано на рис. 3.2.
Решение В определении денежной отдачи для каждой ветви необходимо вычесть $5000 для тех ветвей дерева, где исследования проводились, т. е. для шести ветвей.
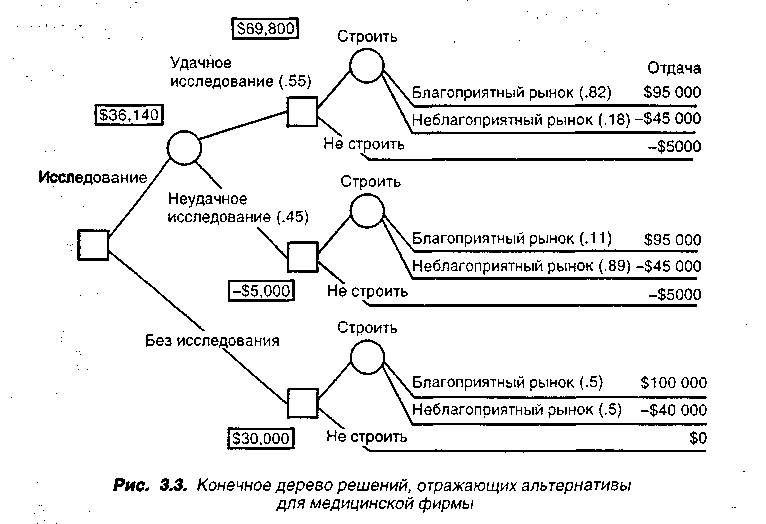
Далее, когда отдача определена для каждого исхода, или ветви дерева решений, следующий шаг состоит в установлении вероятностей каждого состояния внешней среды (см. рис. 3.3). Такие вероятности должен определить менеджер, принимающий решение на рынке. Тогда мы можем анализировать полностью дерево решений.
И з решения, отраженного на рис. 3.3, очевидно, что группа исследования рынка приглашается. Если исследование благоприятное, клиника должна быть построена, если нет, то клинику строить не будут. Решение с участием маркетинговой группы дает отдачу $36140, а без участия исследователей и при строительстве клиники приносит $30000. Тогда лучшее решение – проводить исследование и принимать решение на основе полученных рекомендаций.
Задача 3.3. Для каждой альтернативы мы считаем ожидаемую стоимостную оценку (EMV) — максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов.
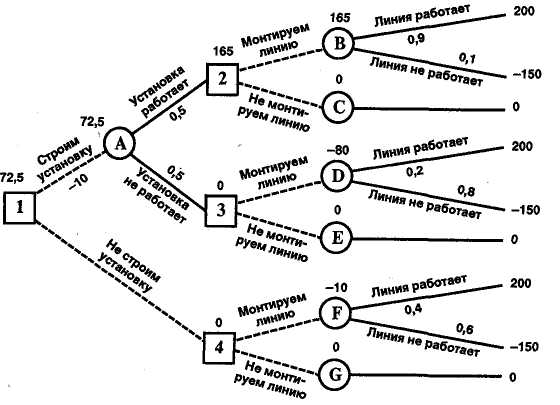
Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения?
В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150) => оценка узла F: EMV(F) = 0,4X200 + 0,6х(-150) = -10. Это число мы пишем над узлом F.
В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV(F) = -10) и решением «не монтируем линию» (оценка этого решения EMV((G) = 0): EMV(4) = max = max = 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем.
EMV(B) = 0,9*200 + 0,1*(-150) = 180 — 15 = 165
EMV(2) = max = max = 165 = EMV(B). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию».
EMV(.D) = 0,2*200 + 0,8*(-150) = 40 — 120 = -80.
E MV(E) = 0.
EMV(3) = max = max = 0 = EMV(E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию».
EMV(A) = 0,5*165 + 0,5*0 — 10 = 72,5.
Поэтому в узле 1 отбрасываем возможное решение «не строим установку».
Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо.
Источник