Дерево решений рисков расчеты

Принятие решений в условиях риска. Дерево решений

Тема 3 Принятие решений в условиях риска 3.1 Дерево решений Рассмотренная ранее ситуация подразумевала, что ЛПР обладает полной информацией (своими оценками или экспертизами) о рассматриваемой проблеме. Однако, часто бывает, когда степень привлекательности альтернативы по тому или иному критерию зависит от случайных факторов. Если ЛПР не знает, как развернется ситуация по той или иной альтернативе при принятии решения, но имеются объективные вероятности развития возможных ситуаций, то такую математическую модель будем называть моделью принятия решений в условиях риска. При анализе такой модели удобно пользоваться графическим представлением, называемым деревом решений. Дерево решений представляет собой граф (графическую схему), которая состоит из дуг (линий), каждая из которых соответствует возможному варианту развития ситуации, и вершин, изображаемых окружностями или квадратами, каждая из которых соответствует «развилке», когда развитие ситуации может принять тот или иной сценарий. Дерево строится слева направо, начиная с корневой ветки, которая соответствует началу принятия решения. Если при развитии какой либо ситуации возможны несколько вариантов ее реализации, при этом выбор варианта осознанно осуществляет ЛПР, то на дереве событий эту «развилку» будем обозначать квадратом. Если же выбор варианта развития ситуации осуществляется благодаря случаю и ЛПР на него не влияет, то такую «развилку» будем обозначать окружностью. Под каждой линией указывается вероятность реализация соответствующему этой линии сценарию развития ситуации. Таким образом, все возможные сценарии развития событий будут отображены на дереве решений в виде ветвей этого дерева. Последние правые ветви дерева решений соответствуют конкретным исходам, результатам принятого решения. В большинстве случаев этот результат можно измерить количественно, например, если он имеет смысл прибыли, вероятности успеха, степени риска. Если показатель привлекательности результата качественный, то его можно измерить путем экспертной оценки. Проставим в конце правых крайних ветвей дерева показатели их привлекательности, которые назовем весами этих ветвей. На следующем этапе нужно проставить веса остальных ветвей. Процесс взвешивания производится справа налево, от крайних ветвей дерева к их корню. При этом нужно соблюдать следующие правила: 1. Если взвешиваемая ветка расходится на несколько в результате принятого ЛПР решения (развилка – квадрат), то вес ветки равен максимальному весу веток, исходящих из нее, при этом ветки с меньшими весами обрубаются. 2. Если взвешиваемая ветка расходится из-за случайных обстоятельств (развилка — круг), то ее вес равен сумме произведений весов всех исходящих из нее веток, умноженных на вероятности этих веток. 3. Если какая-либо ветка имеет дополнительных вес (например из-за промежуточных дополнительных затрат), то этот вес добавляется к рассчитанному. Взвешивание веток производится до тех пор, пока не будет взвешена последняя левая корневая ветка. Ее вес и есть средний выигрыш ЛПР, если он будет действовать оптимально, принимая решения по «неотрубленным» веткам дерева решений. 3.2 Примеры решения задач Пример 3.1 Главному инженеру компании надо решить, монтировать или нет новую производственную линию, использующую новейшую технологию. Если новая линия будет работать безотказно, компания получит прибыль 200 млн. рублей. Если же она откажет, компания может потерять 150 млн. рублей. По оценкам главного инженера, существует 60% шансов, что новая производственная линия откажет. Можно создать экспериментальную установку, а затем уже решать, монтировать или нет производственную линию. Эксперимент обойдется в 10 млн. рублей. Главный инженер считает, что существует 50% шансов, что экспериментальная установка будет работать. Если экспериментальная установка будет работать, то 90% шансов за то, что смонтированная производственная линия также будет работать. Если же экспериментальная установка не будет работать, то только 20% шансов за то, что производственная линия заработает. Следует ли строить экспериментальную установку? Следует ли монтировать производственную линию? Какова ожидаемая стоимостная оценка наилучшего решения? Дерево решений представлено на рисунке 3.1. Места, где принимаются решения, обозначают квадратами □, места появления случайных исходов — кругами ○, возможные решения — пунктирными линиями ———, возможные исходы — сплошными линиями ——. Для каждой альтернативы считаем ожидаемую стоимостную оценку (EMV) — максимальную из сумм оценок выигрышей, умноженных на вероятность реализации выигрышей, для всех возможных вариантов. Рисунок 3.1 – Дерево решений к примеру 3.1. В узле F возможны исходы «линия работает» с вероятностью 0,4 (что приносит прибыль 200) и «линия не работает» с вероятностью 0,6 (что приносит убыток -150) => оценка узла F: EMV( F) = 0,4 * 200 + 0,6 * (-150) = -10. Это число мы пишем над узлом F. EMV(G) = 0. В узле 4 мы выбираем между решением «монтируем линию» (оценка этого решения EMV( F) = -10) и решением «не монтируем линию» (оценка этого решения EMV(G) = 0): EMV(4) = max = max = 0 = EMV(G). Эту оценку мы пишем над узлом 4, а решение «монтируем линию» отбрасываем и зачеркиваем. Аналогично: EMV( B) = 0,9 *200 + 0,1 * (-150) = 180 — 15 = 165. EMV(С) = 0. EMV(2) = max = max = 165 = EMV(5). Поэтому в узле 2 отбрасываем возможное решение «не монтируем линию». EM V(D) = 0,2 * 200 + 0,8 * (-150) = 40 — 120 = -80. EMV( E) = 0. EMV(3) = max = max = 0 = EMV( E). Поэтому в узле 3 отбрасываем возможное решение «монтируем линию». ЕМ V( A) = 0,5 * 165 + 0,5 * 0 — 10 = 72,5. EMV(l) = max = max = 72,5 = EMV( A). Поэтому в узле 1 отбрасываем возможное решение «не строим установку». Ожидаемая стоимостная оценка наилучшего решения равна 72,5 млн. рублей. Строим установку. Если установка работает, то монтируем линию. Если установка не работает, то линию монтировать не надо. Пример 3.2 Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий. A. Построить большой завод стоимостью M1 = 700 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере R1 = 280 тысяч долларов в течение следующих 5 лет) с вероятностью p1 = 0,8 и низкий спрос (ежегодные убытки R2 = 80 тысяч долларов) с вероятностью р2 = 0,2. Б. Построить маленький завод стоимостью М2 = 300 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере T1= 180 тысяч долларов в течение следующих 5 лет) с вероятностью p1 = 0,8 и низкий спрос (ежегодные убытки Т2 = 55 тысяч долларов) с вероятностью р2 = 0,2. B. Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p3 = 0,7 и p4 = 0,3 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p5 = 0,9 и р6 = 0,1 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет. Все расчеты выражены в текущих ценах и не должны дисконтироваться. Нарисовав дерево решений (рисунок 3.2.), определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах. Рисунок 3.2 – Дерево решений к примеру 3.2. Ожидаемая стоимостная оценка узла А равна ЕМ V(А) = 0,8 х 1400 + 0,2 х (-400) — 700 = 340. EMV( B) = 0,8 х 900 + 0,2 х (-275) — 300 = 365. EMV( D) = 0,9 x 1120 + 0,1 x (-320) — 700 = 276. EMV(E) = 0,9 x 720 + 0,1 х (-220) — 300 = 326. EMV(2) = max = max = 326 = EMV( E). Поэтому в узле 2 отбрасываем возможное решение «большой завод». EMV( C) = 0,7 x 326 + 0,3 x 0 = 228,2. EMV(1) = max = max = 365 = EMV( B). Поэтому в узле 1 выбираем решение «маленький завод». Исследование проводить не нужно. Строим маленький завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 365 тысяч долларов. 3.3 Матрица выигрышей и матрица риска ЛПР. Критерий Байеса Ситуацию принятия решений в условиях риска иногда удобно представить в виде, так называемой, матрицы выигрышей ЛПР. Предположим, что ЛПР имеет m альтернатив решения ситуации, которые обозначим A1, A2, . , Am. Результат выбора (выигрыш ЛПР) зависит от того, как будит развиваться ситуация, на которую ЛПР повлиять никак не может. Предположим, что ЛПР выделяет n вариантов развития ситуации, которые обозначим S1, S2. , Sn. Данные варианты в теории принятия решений называют «Состояниями природы», т.к. в большинстве реальные задачи этого типа связаны с погодными, климатическими, экономическими, социальными и другими неопределенностями. Допустим, что известен результат (выигрыш) для ЛПР, выраженный количественно при каждой альтернатива Ai и развитии ситуации Sj. Обозначим его aij. Получаем матрицу A = , которую называют матрицей выигрышей. Или в виде таблицы: Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть j-я , то было бы принято решение, дающее доход aij. Значит, принимая i-e решение, мы рискуем получить не максимально возможный выигрыш ai= , а только aij. Значит принятие i-го решения несет риск недобрать rij = — aij = ai — aij. Матрица R= называется матрицей рисков. Пример 3.3 Пусть матрица выигрышей есть Составим матрицу рисков. Имеем a1 = max(ai1) = 8, a2 = 12, a3 = 10, a4 = 8. Следовательно, матрица рисков есть Критерием принятия решений в условиях неопределенности может быть критерий Байеса. Он основан на предположении, что известна вероятность для каждого варианта развития ситуации (состояния «природы») Sj и она равна pj (. Поэтому, для принятия решения, необходимо рассчитать функцию полезности Fi для каждой альтернативы, равную по сути математическому ожиданию показателей привлекательности по каждому «состоянию природы»: Выбирается та альтернатива, для которой функция полезности максимальна. С другой стороны, если задана матрица рисков R=, то согласно критерию Байеса следует выбрать ту альтернативу, для которой математическое ожидание риска минимально. Заметим, что, анализируя дерево решений и выбирая лучшие альтернативы, по сути руководствуются критерием Байеса. Контрольные вопросы 1) Приведите содержательные примеры ситуаций выбора в условиях риска. В придуманных вами примерах опишите множество альтернатив ЛПР и множество возможных «состояний природы». 2) Каковы способы задания ситуаций в условиях риска? 3) Какой содержательный смысл имеют элементы матрицы рисков? 4) Что такое ожидаемая стоимостная оценка решений? 5) В чем заключается критерий Байеса? 6) Как строится «дерево решений»?

Поделись лекцией и получи промокод на скидку 30% на платформе Автор24

Заполни поля и прикрепи лекцию. Мы вышлем промокод со скидкой тебе на почту

Источник

Управление рисками

Одним из способов оценки рисков является дерево решений, которое представляет собой иерархическую последовательную структуру. Каждому определенному объекту соответствует исключительно единственный узел. Данный метод используется для прогнозирования в условиях риска и неопределенности.

Итак, дерево решений является инструментом управления последовательными рисками.

Оно включает в себя:

Этапы разработки дерева решений:

1. Разделить анализ на отдельные фазы риска
2. Оценить вероятность результатов на каждой отдельной фазе
3. Определить точки принятия решений
4. Вычислить денежные потоки/стоимость в конечных узлах
5. Пройти дерево решений в обратном порядке

Плюсы дерева решений:

• быстрый процесс обучения;
• ясная классификационная модель;
• высокая точность прогноза, которая сопоставима также и с другими методами, такие как статистика или нейронные сети;
• построение непараметрических моделей.

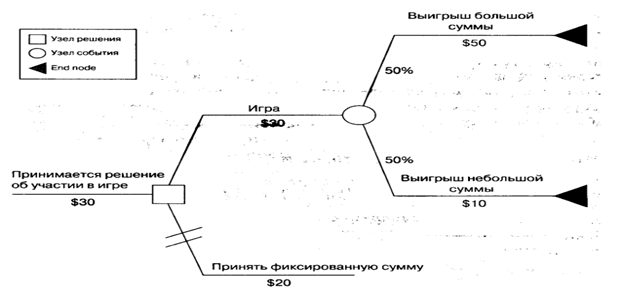
Таким образом, как следует думать при построении дерева решений: если — то. В нашем примере: если мы принимаем решение об участии в игре, то у нас есть два исхода: первый — мы играем и в конечном итоге есть вероятность 50%, что мы выиграем 50 долларов, что на 20 долларов больше, нежели у нас было изначальное, второй исход: мы принимаем фиксированную сумму 20 долларов.

Области, где может применяться дерево решений:

1. Банковское дело, здесь можно произвести оценку кредитоспособности клиентов банка при выдаче им кредитов.
2. Промышленность, здесь можно произвести контроль качества продукции, т.е. выявить количество брака, дефектов.
3. Медицина, здесь можно произвести диагностику болезней.
4. Молекулярная биология, здесь можно проанализировать строение аминокислот.
5. Бизнес, здесь можно спрогнозировать, насколько выгоден тот или иной проект. Если говорить о дереве решений при оценке проектов, то здесь следует рассчитывать NPV (net present value) — чистую приведенную стоимость.

Дерево решений — это теория игр, раздел прикладной математики, который с точки зрения математики помогает строить прогнозы.

Источник