Дерево решений системный анализ

5.1.4. Анализ и решение задач с помощью дерева решений

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов.

Этап 1. Формулирование задачи. Прежде всего необходимо отбросить не относящиеся к проблеме факторы, а среди множества оставшихся выделить существенные и несущественные. Это позволит привести описание задачи принятия решения к форме, поддающейся анализу.

Должны быть выполнены следующие основные процедуры:

• определение возможностей сбора информации для экспериментирования и реальных действий;
• составление перечня событий, которые с определенной вероятностью могут произойти;
• установление временного порядка расположения событий, в исходах которых содержится полезная и доступная информация, а также тех последовательных действий, которые можно предпринять.

5.1.5. Пример процедуры принятия решения

Прототипом данного примера может служить реальный проект, реализованный в Москве. Пример 5.3. Руководство инвестиционной компании при выборе большого земельного участка для вложения своих (и привлеченных) средств решает:

• создавать ли на нем крупный культурно-оздоровительный комплекс с магазинами и предприятиями бытового обслуживания (проект «Аквадром»);
• вложить деньги в гаражное строительство (проект «Гараж»);
• отказаться от проекта вообще и использовать другие формы вложения денег (проект «Депозит»).

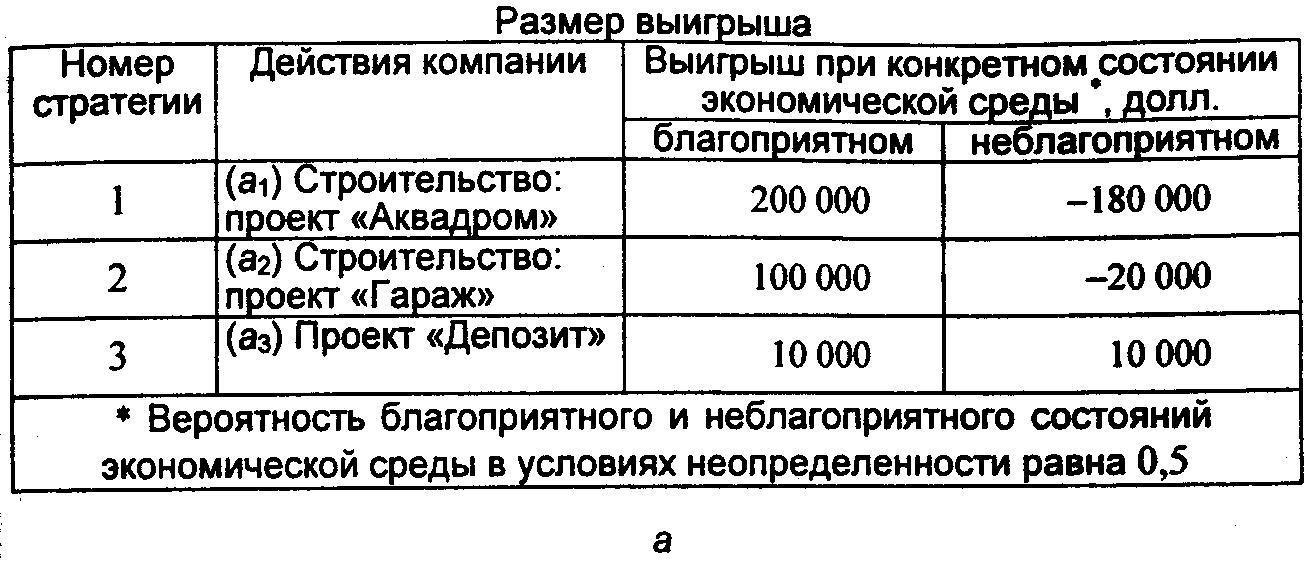
Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка городских услуг (рис. 5.1, а). На основе таблицы выигрышей (потерь) можно построить дерево решений (рис. 5.1, б).Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО. Определим средний ожидаемый выигрыш (ОДО). Результаты показаны в табл. 5.2. Таблица 5.2Определение ожидаемого выигрыша

Вершина	Расчетное выражение, долл.	Выигрыш, долл.
Вершина 1, ОДО1	0,5 •200 000 + 0,5 (-180 000)	10000
Вершина 2, ОД02	0,5 •100 000 + 0,5 (-20 000)	40000
Вершина 3, ОД03	—	10000

Вывод. Наиболее целесообразно выбрать стратегию а₂, т.е. выбрать проект «Гараж», а ветви (стратегии) a₁ и а₃ дерева решений можно отбросить. ОДО наилучшего решения равна 40 000 долл. Следует отметить, что наличие состояния с вероятностями 50 % неудачи и 50 % удачи на практике часто означает, что истинные вероятности игроку скорее всего неизвестны и он всего лишь принимает такую гипотезу (так называемое предположение fifty-fifty , т.е. «пятьдесят на пятьдесят»). Усложним рассмотренную выше задачу. Пусть, перед тем как принимать решение о строительстве (или об отказе от него), руководство компании должно определить, заказывать дополнительное исследование состояния рынка городских услуг или нет. Причем предоставляемая услуга обойдется компании в 10 000 долл. Руководство понимает, что дополнительное исследование по-прежнему не способно дать точной информации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей. Относительно маркетинговой фирмы, которой можно заказать прогноз, известно, что она способна уточнить значения вероятностей благоприятного или неблагоприятного исхода. Возможности этой фирмы в виде условных вероятностей благоприятности и неблагоприятности рынка представлены на рис. 5.2, а. Например, когда фирма утверждает, что рынок благоприятный, то с вероятностью 0,78 этот прогноз оправдывается (с вероятностью 0,22 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,73. Предположим, что маркетинговая фирма, которой заказали прогноз состояния рынка, сделала следующий прогноз:

• ситуация будет благоприятной с вероятностью 0,45;
• ситуация будет неблагоприятной с вероятностью 0,55.

На основании дополнительных сведений можно построить новое дерево решений (рис. 5.2,6), где развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным. Выводы. Необходимо проводить дополнительное исследование конъюнктуры рынка, поскольку это позволяет существенно уточнить принимаемое решение. Если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно выбрать проект «Аквадром» (ожидаемая максимальная прибыль 116 400 долл.), если прогноз неблагоприятный — проект «Гараж» (ожидаемая максимальная прибыль 12 400 долл.). Определим ожидаемую ценность точной информации. Предположим, что консалтинговая фирма за определенную плату готова предоставить информацию о фактической ситуации на рынке в тот момент, когда руководству компании надлежит принять решение о выборе проекта. Принятие предложения этой консалтинговой фирмы зависит от соотношения между ожидаемой ценностью (результативностью) точной информации и величиной запрошенной платы за дополнительную (истинную) информацию, благодаря которой может быть откорректировано принятие решения, т.е. первоначальное действие может быть своевременно изменено. Ожидаемая ценность точной информации о фактическом состоянии рынка равна разности между ожидаемой денежной оценкой при наличии точной информации и максимальной ожидаемой денежной оценкой при отсутствии точной информации. Рассчитаем ожидаемую ценность точной информации для примера, в котором дополнительное обследование конъюнктуры рынка не проводится. При отсутствии точной информации, как уже было показано выше, максимальная ожидаемая денежная оценка равна: ОДО = 0,5 • 100 000 — 0,5 • 20 000 = 40 000 долл. Если точная информация об истинном состоянии рынка будет благоприятной (ОДО = 200 000 долл., см. рис. 5.1, а), принимается решение в пользу проекта «Аквадром»; если неблагоприятной, то наиболее целесообразное решение — это проект «Депозит» (ОДО = 10 000 долл.). Учитывая, что вероятности благоприятной и неблагоприятной ситуаций равны 0,5, значение ОДО точной информации (ОДО_ти) определяется выражением: ОДО_т.и = 0,5 • 200 000 + 0,5•10 000 = 105 000 долл. Тогда ожидаемая ценность точной информации ОЦ_т.и равна: ОЦ_т.и = ОДО_т.и — ОДО = 105 000 — 40 000 = 65 000 долл. Значение ОЦ_т.и показывает, какую максимальную цену должна быть готова заплатить компания за точную информацию об истинном состоянии рынка в тот момент, когда ей это необходимо. При явной эффективности рассмотренной выше многоэтапной процедуры принятия решений следует отметить два обстоятельства, усложняющие ее применение на практике: 1) вероятности «ветвления» по дереву решений зачастую определяются экспертами консалтинговых фирм, причем необходимы дополнительные эксперты-аудиторы, которые оценивали бы надежность работы таких фирм; 2) прибыли (убытки) невозможно просчитать только по сметам бизнес-плана проекта; эти прибыли (убытки) зависят от сроков и динамики реализации проекта.

Источник

Как увидеть лес за деревьями: что такое Decision Tree и зачем это нужно в Big Data

Продолжая насыщать курс Аналитика больших данных для руководителей важными понятиями системного анализа, сегодня мы рассмотрим, что такое дерево решений (Decision Tree). А также расскажем, как этот метод Data Mining и предиктивной аналитики используется в машинном обучении, экономике, менеджменте, бизнес-анализе и аналитике больших данных.

Как растут деревья решений: базовые основы

Начнем с определения: дерево решений – это математическая модель в виде графа, которая отображает точки принятия решений, предшествующие им события и последствия. Этот метод Data Mining широко используется в машинном обучении, позволяя решать задачи классификации и регрессии [1].

Аналитические модели в виде деревьев решений более вербализуемы, интерпретируемы и понятны человеку, чем другие методы Machine Learning, например, нейронные сети. Дополнительное достоинство Decision Tree – это быстрота за счет отсутствия этапа подготовки данных (Data Preparation), поскольку не нужно очищать и нормализовать датасет [2].

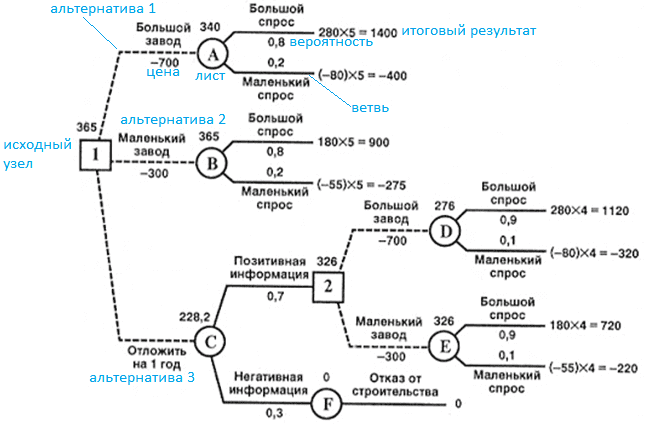
В бизнес-анализе, менеджменте и экономике Decision Tree – это отличный инструмент для наглядного отображения всех возможных альтернатив (сценариев), прогнозирования будущих событий, а также оценки их потенциальной выгоды и рисков. Для этого дерево решений представляют в виде графической схемы, чтобы его проще воспринимать и анализировать. Данный граф состоит из следующих элементов [3]:

• вершины, от которых возможно несколько вариантов, называют узлами. Они показывают возможные ситуации (точки принятия решений);
• конечные узлы (листья) представляют результат (значение целевой функции);
• ребра (ветви), соединяющие узлы, описывают вероятности развития событий по этому сценарию.

Обычно многоузловые деревья решений строятся с помощью специального программного обеспечения. Но граф с ограниченным числом вершин можно построить в табличном редакторе или даже вручную. Как это сделать самостоятельно, мы рассмотрим далее на простом примере из управленческой практики.

Строим дерево решений на примере обучения Big Data

Итак, проанализируем кейс построения дерева решений на примере расчета выгоды от обучения сотрудников новой Big Data технологии с целью быстрого выпуска продукта ценой X. При этом возможны следующие альтернативные сценарии:

• поручить каждому сотруднику самостоятельно освоить нужные подходы, фреймворки и языки программирования в свободное от работы время. Фактические затраты на реализацию такого решения равны нулю, а вероятность успешного освоения технологии для быстрого выпуска продукта оценивается на уровне 30%.
• выделить w рабочих дней на самостоятельное обучение каждого сотрудника на его рабочем месте. Фактические затраты на реализацию такого решения составляют стоимость рабочего дня каждого сотрудника в день (Z), умноженное на количество дней (w) и число сотрудников (k). Успех ожидается в 50% случаев.
• организовать корпоративное обучение всех сотрудников в специализированном учебном центре в течении n дней. Затраты на обучения составят совокупную стоимость курсов (Y), а также цену рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k). При этом сотрудники освоят технологию с вероятностью 98% за n дней (n

Затраты на реализацию решения

Вероятность успешного освоения технологии для быстрого выпуска продукта ценой X

Самостоятельное обучение каждого сотрудника вне работы

Самостоятельное обучение каждого сотрудника на работе

стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (w)*число сотрудников (k)

Организованные курсы для всех сотрудников в учебном центре

цена обучения (Y) + стоимость рабочего дня каждого сотрудника в день (Z)*количество дней (n)*число сотрудников (k)

Сравнив в абсолютных числах выражения 0,3X, (X*0,5 – Z*w*k) и (X*0,98 – Y – Z*n*k), можно выбрать наиболее выгодный вариант. Таким образом, дерево решений позволяет количественно оценить риски, затраты и выгоды возможных альтернатив и выработать оптимальную управленческую стратегию. Не случайно профессиональный стандарт бизнес-аналитика, руководство BABOK, о котором мы рассказывали здесь, включило дерево решений в набор наиболее часто используемых техник [4]. В следующей статье мы расскажем, как деревья решений и другие методы интеллектуального анализа данных реализуются в новом тренде аналитики больших данных — Augmented Analytics.

Источник