Дерево решений варианты альтернативы

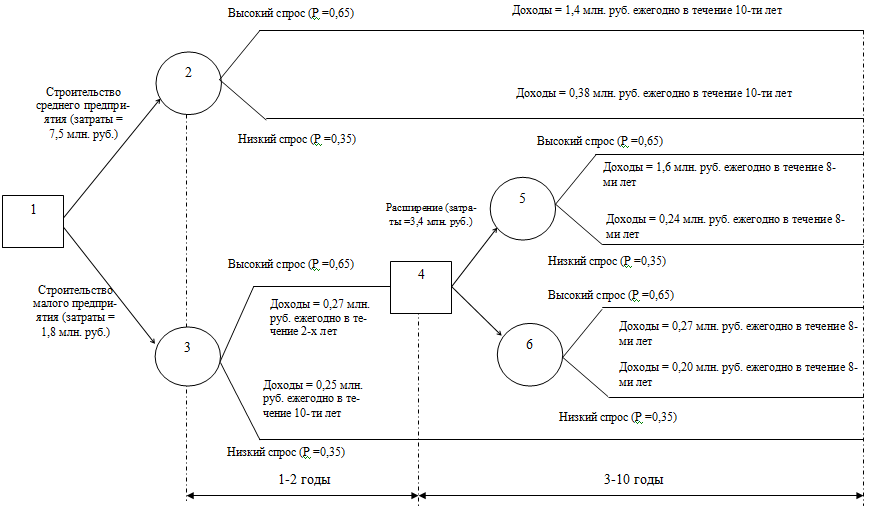
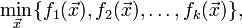16. Генерация альтернатив решений: Дерево решений

Дерево решений – это граф, представляющий правила в иерархической последовательной структуре, где каждому объекту соответствует единственный узел, дающий решение. Дерево решений обычно строится следующим образом. Сначала берется весь набор данных, который представляется исходной или корневой вершиной. Затем определяются способы (правила) разбиения на ветви всего множества записей или вариантов, соответствующих корневому узлу. Ветви образуют дерево, повернутое кроной вниз. На ветвях дерева отмечают узлы, отвечающие подмножеству записей или вариантов. На каждом узле снова определяются правила разбиения на ветви и т.д. до тех пор, пока процесс не дойдет до конечных узлов, называемых листьями. В связи с этим, деревья решений часто применяются для моделирования (генерации) «многоэтапных» процессов принятия решений, в которых взаимозависимые решения принимаются последовательно. Такое представление облегчает описание процесса принятия решений. Для генерации различных вариантов решений и их оценки наибольшее распространение получили деревья решений, содержащие два типа вершин: вершины в которых решение принимает эксперт (ЛПР) и вершины где решение принимает «случай», выходящие из вершины дуги задают определенные вероятности направлений принятия решения.

17. Многокритериальная оптимизация. Проблемы многокритериальной оптимизации

Многокритериальная оптимизацияилипрограммирование— это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения.

Задача многокритериальной оптимизации формулируется следующим образом: [3]

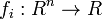
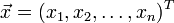
где это() целевых функций. Векторы решенийотносятся к непустой области определения.

Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.

Принятие решения — это выбор альтернативы, которая одновременно удовлетворяет и нечетким целям, и нечетким ограничениям. В этом смысле, цели и ограничения являются симметричными относительно решения, что стирает различия между ними и позволяет представить решение как слияние нечетких целей и ограничений.

Рис. 14.1 — К примеру 14.1: принятие решения по принципу Беллмана-Заде

При принятии решений по схеме Беллмана-Заде не делается никакого различия между целью и ограничениями. Всякое разделение на цель и ограничения является условным.

Нечеткий многокритериальный анализ вариантов

— множество вариантов, которые подлежат многокритериальному анализу;

— множество количественных и качественных критериев, которыми оцениваются варианты.

Задача многокритериального анализа состоит в упорядочивании элементов множества X по критериям из множества G.

Пусть — число в диапазоне [0,1], которое характеризирует уровень оценки вариантапо критерию: чем больше число, тем выше оценка вариантапо критерию,,. Тогда критерийможно представить в виде нечеткого множествана универсальном множестве вариантов X:

,

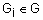
где — степень принадлежности элементанечеткому множеству.

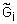
Находить степени принадлежности нечеткого множества (14.5) удобно методом построения функций принадлежности на основе парных сравнений. При использовании этого метода необходимо сформировать матрицы парных сравнений вариантов по каждому критерию. Общее количество таких матриц совпадает с количеством критериев и равняется n.

Наилучшим вариантом будем тот, который одновременно лучший по всем критериям. Нечеткое решение находится как пересечения частных критериев:

Согласно с полученным нечетким множеством ‚ наилучшим вариантом следует считать тот‚ для которого степень принадлежности является наибольшей.

При неравновесных критериях формула (14.6) принимает вид:

,

где — коэффициент относительной важности критерия,.

Показатель степень в формуле (14.7) свидетельствует о концентрации нечеткого множествав соответствии с мерой важности критерия. Коэффициенты относительной важности критериев могут быть определены различными методами, например, с помощью парных сравнений по шкале Саати.

Источник

Дерево решений

Пример №1 . Требуется принять решение о замене старого оборудования на новое того же вида или его ремонте. Отремонтированное оборудование впоследствии можно частично заменить на новое, более современное, или отремонтировать его заново.
Решение определяется будущим спросом на продукцию, которую производят на этом оборудовании.
Полная замена оборудования экономически оправдана при высоком уровне спроса. С другой стороны, можно отремонтировать старое оборудование и через один год, например, заменить его на новое, более совершенное, или заново его отремонтировать.
В данной задаче процесс принятия решения состоит из двух этапов: решение в настоящий момент времени о замене или ремонте оборудования и решение, принимаемое через один год, относительно частичной его замены и ремонта.
Предполагается, что спрос может оказаться высоким, средним и низким.
Дерево решений имеет два типа вершин: «решающие» и «случайные» (рис.).

Рис. Дерево решений
Начиная с «решающей» вершины 1, необходимо принять решение о полной замене оборудования или его ремонте.
Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность установления более совершенного оборудования или повторного ремонта старого в том случае, если спрос по истечении одного года установится на высоком уровне. Поэтому в вершине 4 принимается решение о частичной замене старого оборудования более совершенным или ремонте старого. Вершины 5 и 6 «случайные».
Допускается, что фирма рассматривает эту задачу на пятилетний период. Анализ рыночной ситуации показывает, что вероятности высокого, среднего и низкого уровней спроса составляют соответственно 0,6, 0,3 и 0,1. Замена новым оборудованием того же вида, что и старое, обойдется в 2,5 млн р., а ремонт старого – в 0,8 млн р.
Затраты на частичную замену оборудования более совершенным оцениваются в 1,5 млн р., а повторный ремонт старого – в 0,8 млн р.
Ежегодные доходы для каждой стратегии фирмы следующие.
1. Замена старого оборудования на новое того же вида при высоком, среднем и низком уровнях спроса даёт соответственно 0,95, 0,7 и 0,45 млн р.
2. Ремонт старого оборудования при высоком, среднем и низком уровнях спроса оценивается соответственно в 0,3, 0,15 и 0,1 млн р.
3. Частичная замена оборудования на более совершенное при высоком, среднем и низком уровнях спроса составит соответственно 0,9, 0,6 и 0,4 млн р.
4. Повторный ремонт старого оборудования при высоком, среднем и низком уровнях спроса предполагает 0,3, 0,2 и 0,1 млн р. соответственно.
Определим оптимальную стратегию фирмы в замене оборудования.

Решение.
Оценим результаты каждой стратегии и определим, какие решения следует принимать в «решающих» вершинах 1 и 4.
Вычисления начнем с этапа 2. Для последних 4 лет альтернативы, относящиеся к вершине 4, оцениваются так:
ДЧЗ = (0,9 × 0,6 + 0,6 × 0,3 + 0,4 × 0,1) × 4 – 1,5 = 1,54 млн р.,
ДДР = (0,3 × 0,6 + 0,2 × 0,3 + 0,1 × 0,1) × 4 – 0,8 = 0,2 млн р.,
где ДЧЗ – доход от частичной замены оборудования на более совершенное; ДДР – доход от замены оборудования, прошедшего дважды ремонт.
Так как ДЧЗ > ДДР , то в вершине 4 выгоднее частично заменить оборудование на более совершенное, при этом доход составит 1,54 млн р.
Для дальнейших расчетов в вершине 4 можно оставить одну ветвь, которой соответствует доход в 1,54 млн р. за 4 года.
Вычислим доходы на 1-м этапе для «решающей» вершины 1:
ДЗН = (0,95 × 0,6 + 0,7 × 0,3 + 0,45 × 0,1) × 5 – 2,5 = 1,625 млн р.,
ДЗО = 0,3 × 0,6 × 1 + 0,15 × 0,3 × 5 + 0,1 × 0,1 × 5 +1,54 – 0,8 = 1,195 млн р.,
где ДЗН – доход от замены старого оборудования на новое того же вида; ДЗО— доход от отремонтированного оборудования и дальнейшей замены на более совершенное.
Так как ДЗН > ДЗО , то оптимальным решением в вершине 1 является полная замена старого оборудования на новое того же вида.
Итак, оптимальной стратегией фирмы в замене оборудования является полная замена старого оборудования на новое того же вида, при этом доход составит 1,625 млн р.

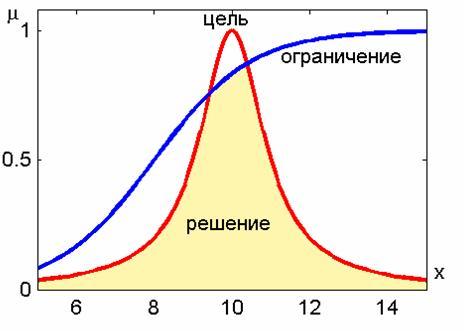
• среднее предприятие при высоком (низком) спросе – F=1,4 (K=0,38) млн. руб.;
• малое предприятие при низком спросе – L=0,25 млн. руб.;
• малое предприятие при высоком спросе – М=0,27 млн. руб.;
• расширенное предприятие при высоком (низком) спросе дает N=1,6 (P=0,24) млн. руб.;
• малое предприятие без расширения при высоком спросе в течение первых двух лет и последующем низком спросе дает R=0,2 млн. руб. за остальные восемь лет.

Начиная с вершины 1, являющейся «решающей», необходимо принять решение относительно размера предприятия. Вершины 2 и 3 являются «случайными». Фирма будет рассматривать возможность расширения малого предприятия только в том случае, если спрос по истечении первых двух лет установится на высоком уровне. Поэтому в вершине 4 принимается решение о расширении или не расширении предприятия. Вершины 5 и 6 будут «случайными».
Вычисления начнем со 2-го этапа. Для последних восьми лет альтернативы, относящиеся к вершине 4, оцениваются так:
— доход малого предприятия с последующим расширением:
ДР = (1,6*0,65 + 0,24*0,35)*8 – 3,4 = 5,592 млн. руб.
— доход малого предприятия без расширения
ДБР = (0,27*0,65 + 0,2*0,35)*8 = 1,964 млн. руб.
Таким образом, в вершине 4 выгоднее провести расширение, при этом доход составит 5,592 млн. руб.
Перейдем к вычислениям 1-го этапа. Для вершины 1:
— доход среднего предприятия:
ДС = (1,4*0,65 + 0,38*0,35)*10 – 7,5 = 2,93 млн. руб.
— доход малого предприятия с последующим расширением через 2 года:
ДМ = 5,592 + 0,27*0,65*2 + 0,25*0,35*10 – 1,8 = 5,018 млн. руб.
Сравнивая получаемые в вершине 1 доходы среднего и малого предприятий, видим, что более предпочтительным является вариант строительства малого предприятия с последующим расширением через 2 года.

Источник