Дерево схемы электрических цепей

Некие лекции по элтеху / TOE_2

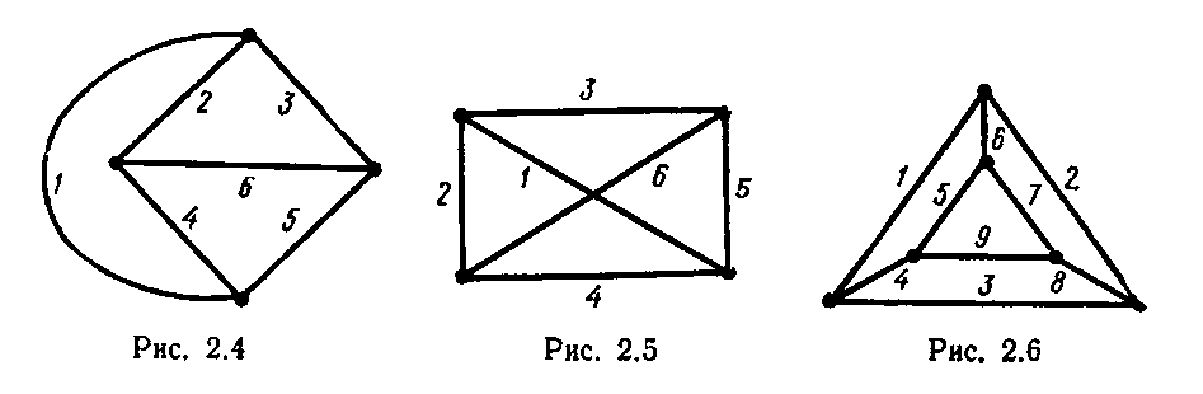
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Например, на рис. 2.3 приведена схема разветвленной электрической цепи. Если .каждую ветвь схемы заменить отрезком линии, получается геометрическая фигура, показанная на рис. 2.4. При этом за ветвь 1 принимается последовательное соединение элементов E₁ и r₁ за ветвь 6 — параллельное соединение элементов r₆ и J₆ и т. д.

Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называют графом электрической цепи. Отрезок линии, соответствующий ветви схемы, называют ветвью графа. Граничные (концевые) точки ветви графа называют узлами графа.

Граф — абстрактное математическое понятие, не обязательно соответствующее электрической цепи. В виде графа могут быть изображены различные природные и технические объекты, например схемы железнодорожных путей, состояния переключающих систем и т. д.

Если в общем случае определить ребро как отрезок линии вместе с его граничными (концевыми) точками, тогда граф можно определить как множество ребер, причем в этом множестве все общие точки ребер являются граничными. Граничную точку ребра называют вершиной.

В электротехнической литературе вместо терминов «ребро» и «вершина» применяют термины «ветвь» и «узел».

Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называют ориентированным. В противном случае граф считают неориентированным.

Граф одной и той же схемы электрической цепи может быть изображен различными способами. Например, граф схемы на рис. 2.3 можно начертить, как это показано на рис. 2.5. Однако топологические свойства графов (рис. 2.4; 2.5) одинаковы. Такие графы называют изоморфными. У изоморфных графов существует взаимно однозначное соответствие между узлами и ветвями. Если некоторая пара узлов в одном графе соединена ветвью, то пара соответствующих узлов в изоморфном графе также должна быть соединена соответствующей ветвью.

Некоторые подграфы графа. Подграфом графа называют часть графа.

Согласно этому определению подграфом может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащееся в данном графе.

В теории электрических цепей большое значение имеют такие подграфы: путь, контур, дерево, связи (дополнение дерева) и сечение. Все определения (пути, контура и т. д.), сформулированные для графа, применимы и к схемам электрической цепи.

Путь —это упорядоченная последовательность ветвей, в которой каждые две соседних ветви имеют общий узел, причем любая ветвь и любой узел встречаются в этом пути только один раз. Например, в графе на рис. 2.6 ветви 4—1—2—8, 4—1—6—7, 4—3—8, 4—3—2—6—7, 5—7, 5—6—2—8 и 9 образуют пути между одной и той же парой узлов (узлов, к которым присоединена ветвь 9).

Контур —замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, в графе на рис. 2.6 ветви 4—1—2—8—9, 5—6—2—8—9, 4—3—8—9 образуют контуры.

Если между любой парой узлов графа (схемы) существует путь, то граф (схему) называют связным (связной).

Деревом связного графа (схемы) называют связный подграф (подсхему), содержащий все узлы графа (схемы), но ни одного контура. Примеры деревьев графа на рис. 2.6 приведены на рис. 2.7.

Ветви графа (схемы), которые дополняют дерево до исходного графа, называют ветвями связи (дополнением дерева). Отдельную ветвь связи называют также главной ветвью. Ветви связи деревьев графа на рис: 2.7 приведены на рис. 2.8.

Если граф (схема) содержит в ветвей и у узлов, то число ветвей любого дерева д=у-1.

Действительно, если число узлов у=2, то дерево может содержать только одну ветвь. Добавление к этой ветви еще одной так, чтобы получился граф без контуров, увеличивает число узлов на единицу и т. д. для каждой новой ветви дерева.

к=в-(у-1)=в—у+1

Сечением графа (схемы) называют множество ветвей, удаление которых делит граф (схему) на два изолированных подграфа (подсхемы), один из которых в частном случае может быть изолированным узлом. Например, для графа на рис. 2.6 ветви 1 — 4 — 3, 1 — 5 — 9 — 3, 1 — 5 — 7 — 2 образуют сечения.

Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примеры таких поверхностей (S₁ S₂, S₃) для графа на рис. 2.6 показаны на рис. 2.9. Поверхность S₁ рассекает граф на две части, одна из которых — изолированный узел.

С понятием дерева связаны понятия главных контуров и главных сечений.

Главным контуром называют контур, состоящий из ветвей дерева и только одной ветви связи. Другими словами, при соединении любой ветви связи с деревом образуется главный контур.

Главным сечением считают сечение, состоящее из ветвей связи и только одной ветви дерева. Каждая ветвь дерева позволяет образовать одно главное сечение.

Для любого выбранного дерева можно образовать свою систему главных контуров и сечений. При этом характерно, что каждый такой контур и каждое сечение будут отличаться от других хотя бы одной ветвью.

На рис. 2.10 и 2.11 показаны главные контуры и сечения, построенные на основе одного из деревьев графа рис. 2.6. Ветви дерева 4—9—7—6—8 отмечены более жирными линиями. Главные контуры (пронумерованы римскими цифрами) образуются ветвями 1—4—9—7—6 (I); 2—8—7‑6 (II); 3—4—9—8 (III); 5—7—9 (IV). Главные сечения содержат ветви 4—1—3 (S₁); 6—1‑2 (S₂); 7—1—5—2 (S₃); 8—2—3 (S₄); 9—1—5—3 (S₅).

Число главных контуров равно числу ветвей связи (к), а число главных сечений — числу ветвей дерева (д).

Первый закон Кирхгофа (равенство (1.12)) справедливо для любого узла или сечения; второй закон Кирхгофа (равенство (1.16)) справедливо для любого контура. Суммирование выполняется для всех ветвей, сходящихся в узле (пересекаемых замкнутой поверхностью) или образующих контур.

Уравнения законов Кирхгофа (1.12) и (1.16) не зависят от типа и свойств элементов, из которых состоят ветви. Это топологические соотношения, которые могут быть составлены по графу цепи или по ее схеме. В дальнейшем при составлении уравнений цепи считается, что направление ветви графа, указанное стрелкой, совпадает с выбранным положительным направлением тока и напряжения ветви схемы (положительные направления тока и напряжения принимаются совпадающими).

В качестве примера можно составить уравнения по законам Кирхгофа для схемы на рис. 2.3, граф которой с указанием выбранных положительных направлений токов и напряжений, а также направлений обхода контуров представлен на рис. 2.12.

На основании первого закона Кирхгофа справедливы уравнения:

На основании второго закона Кирхгофа получаются следующие уравнения:

В записанных уравнениях ток i_k и напряжение u_k обозначают ток и напряжение k-й ветви.

Сложение всех уравнений, записанных по первому закону Кирхгофа, дает тождество 0=0. Аналогичный результат получается при суммировании уравнений, составленных по второму закону Кирхгофа. Таким образом, среди записанных уравнений есть линейно зависимые.

Вместо уравнений по первому закону Кирхгофа для узлов можно составить уравнения по первому закону Кирхгофа для сечений (замкнутых поверхностей). При этом сечению замкнутой поверхности придается ориентация. На рис. 2.13 показаны четыре сечения S₁S₄, для которых справедливы следующие уравнения (за положительные направления принимают направления токов из замкнутых поверхностей):

Уравнение для сечения S₃ отличается от уравнения для сечения S₄ только знаками слагаемых. Следовательно, среди уравнений, составленных для четырех сечений, по крайней мере одно является зависимым.

Вопрос о числе независимых уравнений, которые практически можно составить по законам Кирхгофа, весьма важен. Этот вопрос решают, применяя понятие дерева графа (схемы).

С помощью дерева образуется д главных сечений и к главных контуров. Главные сечения (главные контуры) отличаются друг от друга по крайней мере одной ветвью дерева (одной ветвью связи). Если для главных сечений или для главных контуров составляют уравнения по первому закону Кирхгофа, то они содержат по крайней мере по одному слагаемому, которого нет в других уравнениях. Таким образом, уравнения для главных сечений и главных контуров линейно независимы. Общее число линейно независимых уравнений, составляемых по законам Кирхгофа, равно числу всех ветвей:

д+к=(у-1)+в-(у-1)=в

Таким образом, по первому закону Кирхгофа для сечений составляют

независимых уравнений. Число независимых уравнений, составляемых по второму закону Кирхгофа, равно

Очевидно, что уравнения для сечений получаются как линейные комбинации уравнений для узлов. Например, уравнение для сечения S₂ представляет сумму уравнений для узлов 2 и 3, уравнение для сечения S₃ — сумму уравнений для узлов 1, 2 и 3. В общем случае уравнение для замкнутой поверхности получается суммированием уравнений для узлов, охватываемых этой поверхностью. Следовательно, число независимых уравнений для узлов совпадает с числом независимых уравнений для сечений (2.3).

Из сказанного вытекает значение топологического понятия дерево: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа.

Пример 2.1. Составить независимые уравнения по законам Кирхгофа для графа рис. 2.12.

Решение. Сначала выбираем дерево графа (ветви 2 — 3 — 5). Дерево, главные контуры и сечения показаны на рис. 2.14. За направление обхода контура принимаем направление ветви связи контура, за направление сечения — направление, совпадающее с направлением ветви дерева сечения.

По первому закону Кирхгофа, для сечений

Если за положительное направление тока принять направление к узлу, то уравнения для сечений S₁ и S₃ совпадают с уравнениями для узлов.

По второму закону Кирхгофа,

Источник

Топологические понятия электрических цепей

Основными топологическими понятиями теории электрических цепей являются ветвь, узел, контур, двухполюсник, четырехполюсник, граф схемы электрических цепей, дерево и связь графо схемы. Рассмотрим некоторые из них.
Ветвью называют участок электрической цепи с одним и тем же током. Она может состоять из одного или нескольких последовательно включенных элементов. Так схема цепи на рис.1.7 состоит из пяти ветвей.

Рис.1.7.
Узлом называют место соединения трех и более ветвей. Узел обозначается на схеме точкой. Узлы, имеющие равные потенциалы, объединяются в один потенциальный узел. На схеме рис.1.7 узлы 1’ и 2’ могут быть объединены в один потенциальный узел. Поэтому схема имеет три потенциальных узла.
Контуром называют замкнутый путь, проходящий через несколько ветвей и узлов электрической цепи. Для схемы рис. 1.7 один из контуров включает позиции 2; R5; 2’; R4. Независимым называется контур, в состав которого входит хотя бы одна ветвь, не принадлежащая соседним контурам. Так схема рис.1.7 содержит три независимых контура.
Двухполюсником называют часть электрической цепи с двумя выделенными зажимами — полюсами. Двухполюсник обозначают прямоугольником с индексами А или П. А — активный двухполюсник, в составе которого есть источники ЭДС. П — пассивный двухполюсник. Например, часть схемы рис.1.7 с зажимами а и б может быть представлена двухполюсником (рис.1.8)

Главная страница
ТОЭ
Электрические машины
Физика
Физика Кривченко
Тендер
Исполнительная документация
Приемо-сдаточная документация
Как скачать?
Главному энергетику
Система ППР
Ответственному за электрохозяйство
Ответственному по лифтам
Промышленная безопасность
Охрана труда
Несчастный случай
Пожарная безопасность
Правила и ГОСТы
Бланки и протоколы
Каталоги оборудования
Счётчики
Статьи
Эл. безопасность
Услуги подрядных организаций
Рекламодателям
Заработать
ОТ на пром предприятиях
Билеты по эл. безопасности с ответами

Страница обновлена: 20.12.2022

Отзывы и пожелания можно направлять по адресу energ2010@yandex.ru

Информация предоставлена для ознакомления и не является официальным источником.

Источник