Глава II Деревья
Как показано в § 4, среди графов с фиксированными порядком и числом компонент лишь один имеет максимальное число ребер. Другой крайний случай — минимальное число ребер — приводит к большому классу графов. Наиболее важными среди них являются связные графы, которые называются деревьями. Класс деревьев занимает в теории графов особое положение. С одной стороны, это достаточно просто устроенные графы, и многие задачи, весьма сложные в общей ситуации, для деревьев решаются легко. Доказано, например, что все деревья реконструируемы; несложно распознается изоморфизм деревьев. С другой стороны, деревья часто встречаются в областях, на первый взгляд не имеющих отношения к теории графов.
Деревья открывались независимо несколько раз. Еще в прошлом веке Г. Кирхгоф ввел деревья и применил их к исследованию электрических цепей, а А..Кэли, перечисляя изомеры насыщенных углеводоров, еще раз открыл деревья и первым исследовал их свойства. Тогда же деревья были введены и исследованы К. Жорданом как чисто математический объект.
§ 13. Определение дерева
Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. На рис. 13.1 изображены все деревья шестого порядка.
Существует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.
Теорема 13.1. Для (n, m)-графа G следующие утверждения эквивалентны .
- G — дерево;
- G — связный граф и m = n — 1;
3) G — ациклический граф и m = n — 1; 4) любые две несовпадающие вершины графа G соединяет единственная простая цепь; 5) G — ациклический граф, обладающий тем свойством, что если какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
- => 2) Воспользуемся индукцией по n. При n = 1 утверждение тривиально. Пусть
n > 1, е EG. В дереве G нет циклов, следовательно, согласно лемме 4.8, граф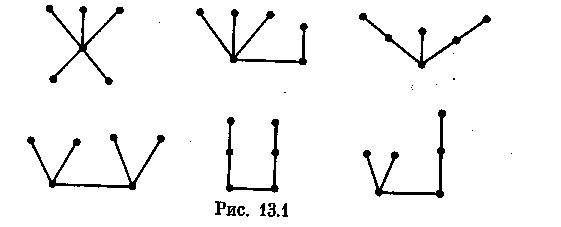 
G — е имеет ровно две компоненты Т1 и T2, каждая из которых есть дерево. Пусть дерево T1 является (ni,mi)-графом, i=1, 2. По индуктивному предположению верно равенство mi = ni— 1. (1) Далее имеем n = m1 + m2 + 1 = (n1 — 1) + (n2 — 1) + 1 = (n1 + n2) — 1 = n — 1. 2) => 3) Граф G связен и m = n — 1. Нужно доказать, что в G нет циклов. Пусть, напротив, в графе G есть цикл, пусть е — ребро этого цикла. Тогда граф G — е связен лемма 4.8) и имеет n — 2 ребра, что противоречит теореме 4.9. Следовательно, G — ациклический граф. 3) => 4) Пусть k — число компонент графа G. Пусть, далее, компонента Ti является (ni, mi)-графом. Так как Ti — дерево, то верно равенство (1). Теперь имеем n— 1 = m = m1 + m2 + . . . + mk =(n1-1) + (n2 — 1)+ . +(nk — 1) = = (n1 + . + nk) — k = n — k, т. е. k = 1. Итак, G — связный граф и потому любые несовпадающие вершины u и v соединены в нем простой цепью. Если бы в G были две несовпадающие простые (u, v)-цепи, то согласно утверждению 4.3 их объединение содержало бы цикл. Следовательно, каждые две вершины соединены единственной простой цепью.
- => 5) Пара несовпадающих вершин, принадлежащих одному циклу, соединена по меньшей мере двумя простыми цепями. Следовательно, граф G ациклический. Пусть u и v — две его несмежные вершины. Присоединим к графу G ребро е = uv. В G есть простая (u, v)-цепь, которая в G + е дополняется до цикла. В силу утверждения 4.4 этот цикл единственный.
- => 1) Нужно доказать, что граф G связен. Если бы вершины u и v принадлежали разным компонентам графа G, то граф G + uv не имел бы циклов, что противоречит утверждению 5). Итак, G связен и потому является деревом.
Следствие13.2. В любом дереве порядка n 2 имеется не менее двух концевых вершин. Пусть d1,d2. dn (2) — степенная последовательность дерева. Тогда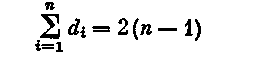 
(лемма о рукопожатиях) и все di > 0. Следовательно, хотя бы два числа из последовательности (2) равны 1. Пусть Н — остовный подграф произвольного графа G. Если на каждой области связности графа G графом Н порождается дерево, то Н называется остовом (или каркасом) графа G. Очевидно, что в каждом графе существует остов: разрушая в каждой компоненте циклы, т. е. удаляя лишние ребра, придем к остову. Остов в графе легко найти с помощью поиска в ширину. Следствие13.3. Число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m(G)—|G|+k(G), где m(G) и k(G)—число ребер и число компонент графа G соответственно. Если (n1, m1)-граф G является одной из компонент графа G, то для превращения ее в остовное дерево нужно удалить m1— (n1 — 1) подходящих ребер. Суммируя по всем k(G) компонентам, получим требуемое. Число v(G)= m(G) — |G| + k(G) называется циклическим рангом (или цикломатическим числом) графа G. Число v*(G)= |G| — k(G) ребер любого остова графа G называется коциклическим рангом графа G. Таким образом, v(G)+v*(G)=m(G). Очевидны три следствия 13.4—13.6. Следствие13.4. Граф G является лесом тогда и только тогда, когда v(G) = 0. Следствие13.5.Граф G имеет единственный цикл тогда и только тогда, когда v(G)= 1. Следствие13.6. Граф, в котором число ребер не меньше, чем число вершин, содержит цикл. В гл. III окажутся полезными утверждения 13.7, 13.8. Утверждение 13.7.Всякий ациклический подграф произвольного графа G содержится в некотором остове графа G. Пусть Н — ациклический подграф в G. Очевидно, что достаточно рассмотреть ситуацию, в которой Н—остовный подграф и G связен. Если теперь Н не является остовом, то он несвязен. Пусть А — одна из областей связности графа Н. В графе G есть такое ребро ab, что а А, b VH\A. Граф Н + аb — ациклический остовный подграф графа G, имеющий меньше, чем Н, компонент. Повторяя аналогичное построение, доберемся до дерева, т. е. остова, содержащего граф Н. Утверждение13.8. Если S и Т — два остова графа G, то для любого ребра е1 графа S существует такое ребро e2 графа Т, что граф S — е1 + е2 также является остовом. Не ограничивая общности, будем считать граф G связным. Граф S — е1 имеет ровно две области связности; пусть это будут А и В. Поскольку граф Т связен, то в нем существует ребро e2, один из концов которого входит в А, а другой — в В. Граф Н = S — е1 + е2 связен и число ребер в нем такое же, как в дереве S. Следовательно, он сам является деревом. Итак, Н— остов графа G. Очевидно, что два предыдущих утверждения об остовах (13.7 и 13.8) сохраняются для произвольного псевдографа. Докажем еще следующую теорему. Теорема 13.9. Центр любого дерева состоит из одной или из двух смежных вершин. Очевидно, что концевые вершины дерева Т являются центральными только для Т = К1 или Т = K2. Пусть Т — дерево порядка n > 2. Удалив из Т все концевые вершины, получим дерево Т’. Очевидно, что эксцентриситет Т’ на единицу меньше эксцентриситета дерева Т и что центры деревьев Т и Т’ совпадают. Далее доказательство легко проводится индукцией по числу вершин.
Источник
1. Деревья. Характеризация дерева.
Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. Существует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.
Теорема 10.1. Для (n, m)--графа G следующие утверждения эквивалентны:
1) G — дерево;
2) G — связный граф и m = n – 1;
3) G — ациклический граф и m = n – 1;
4) любые две несовпадающие вершины графа G соединяет единственная простая цепь;
5) G — ациклический граф, обладающий тем свойством, что если, какую-либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
1) 2) Воспользуемся индукцией по n. При n = 1 утверждение тривиально. Пусть n > 1, e EG. В дереве G нет циклов, следовательно, согласно утверждению 4.5, граф G – e имеет ровно две компоненты T1 и T2, каждая из которых есть дерево. Пусть дерево Ti является (ni, mi)-графом, i = 1, 2. По индуктивному предположению верно равенство
mi = ni – 1 (1)
Далее имеем m = m1 + m2 + 1 = (n1 – 1) + (n2 – 1) + 1 = (n1 + n2 ) – 1 = n – 1.
2) 3) Граф G связен и m = n – 1. Нужно доказать, что в G нет циклов. Пусть, напротив, в графе G есть цикл и пусть e — ребро этого цикла. Тогда граф G – e связен (по утверждению 4.5) и имеет n – 2 ребра, что противоречит теореме 4.6. Следовательно, G — ациклический граф.
3) 4) Пусть k — число компонент графа G. Пусть, далее, компонента Ti является (ni, mi)-графом. Так как Ti — дерево, то верно равенство (1). Теперь имеем n – 1 = m = m1 + m2 +…+ mk = (n1 – 1) + (n2 – 1) +…+ (nk – 1) = (n1 + n2 + …+ nk) – k = n – k, т. е. k = 1. Итак, G — связный граф и потому любые несовпадающие вершины и соединены в нем простой цепью. Если бы в G были две несовпадающие простые (u, v)-цепи, то согласно утверждению 4.1в их объединение содержало бы цикл. Следовательно, каждые две вершины соединены единственной простой цепью.
4) 5) Пара несовпадающих вершин, принадлежащих одному циклу, соединена по меньшей мере двумя простыми цепями. Следовательно, граф G ациклический. Пусть u и v — две его несмежные вершины. Присоединим к графу G ребро e = uv. В G есть простая (u, v)-цепь, которая в G + e дополняется до цикла. В силу утверждения 4.1г этот цикл единственный (иначе в G после выбрасывания e из G + e оставался бы цикл).
5) 1) Нужно доказать, что граф G связен. Если бы вершины u и v принадлежали разным компонентам графа G, то граф G + uv не имел бы циклов, что противоречит утверждению 5 теоремы. Итак, G связен и потому является деревом.
Следствие 10.2. В любом дереве порядка n 2 имеется не менее двух концевых вершин.
Пусть d1, d2, …, dn — степенная последовательность дерева. Тогда d1 + d2 +…+ dn = 2n – 2 (лемма о рукопожатиях) и все di > 0. Следовательно, хотя бы два числа из последовательности степеней вершин равны 1.
Теорема 10.3. Центр любого дерева состоит из одной или из двух смежных вершин.
Доказательство проведем индукцией по числу вершин дерева. Очевидно, что концевые вершины дерева T являются центральными только для T = K1 или T = K2. Пусть T — дерево порядка n > 2. Удалив из T все концевые вершины, получим дерево T’, в котором по предположению индукции центр состоит из одной или из двух смежных вершин. Заметим, что для любой вершины дерева ее эксцентриситет всегда равен расстоянию до некоторой висячей вершины. Тогда эксцентриситет каждой вершины в T’ на единицу меньше ее эксцентриситета в дереве T. Следовательно, центры деревьев T и T’ совпадают.
Пусть H — остовный подграф произвольного графа G. Если в каждой компоненте связности графа G графом H порождается дерево, то H называется остовом (или каркасом) графа G. Очевидно, что в каждом графе существует остов: разрушая в каждой компоненте циклы, т. е. удаляя лишние ребра, придем к остову. Остов в графе легко найти с помощью поиска в ширину.
Следствие 10.4. Число ребер произвольного (n, m)- графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно , где — число компонент связности графа G.
Если (n1, m1)-граф H является одной из компонент графа G, то для превращения ее в остовное дерево нужно удалить m1 – (n1 – 1) подходящих ребер. Суммируя по всем k компонентам, получим требуемое.
Число (G) = m – n + k называется цикломатическим числом графа G. Очевидно следствие
Следствие 10.5. а) граф является лесом тогда и только тогда, когда (G) = 0; б) граф G имеет единственный цикл тогда и только тогда, когда (G) = 1; с) граф, в котором число ребер не меньше, чем число вершин, m n, содержит цикл.
Очевидно, что число остовов в Kn равно числу помеченных деревьев порядка n. В 1897 г. А. Кэли показал, что число помеченных деревьев порядка n равно n n –2 .
Источник