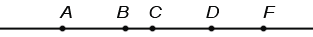Дерево возможных вариантов математика 5 класс

Урок математики в 5 классе по теме: «Дерево возможных вариантов»
план-конспект урока по алгебре (5 класс) по теме

Урок разработан по требованиям Федерального Государственного стандарта на основе УМК линии Сфера.

Скачать:

Предварительный просмотр:

Муниципальное автономное общеобразовательное учреждение

Средняя общеобразовательная школа № 1 имени Сергея Бондарева

Конспект урока по математике в 5 классе

Тема: «Дерево возможных вариантов»

Подготовила и провела: Е,А Роговская

1. Познакомить учащихся с основными приемами подсчета различных вариантов при решении комбинаторных задач;
2. Учить решать комбинаторные задачи с помощью перебора всех возможных вариантов (комбинаций чисел, слов, предметов и др.);
3. формировать умения моделировать ход решения с помощью рисунка, дерева возможных вариантов .

1. развивать математическую речь;
2. развивать умение обобщать, систематизировать, анализировать, сравнивать;
3. развивать внимание;
4. развивать логическое мышление;
5. умение делать выводы.

1. воспитывать интерес к изучению математики;
2. воспитывать самостоятельность;
3. воспитывать желание преодолевать трудности.

1. организовывать свое рабочее место под руководством учителя;
2. определять цель выполнения заданий на уроке;
3. волевая саморегуляция;
4. прогнозирование уровня усвоения;
5. оценка;
6. коррекция.

1. умение осознано строить речевое высказывание в устной форме;
2. отвечать на простые вопросы учителя;
3. построение логической цепи рассуждений;
4. использование индуктивного умозаключения.

1. участвовать в диалоге на уроке;
2. отвечать на вопросы учителя, товарищей по классу;
3. слушать и понимать речь других;

I. Самоопределение к деятельности (орг.момент)

Девиз урока: «Математика – это больше, чем наука, это язык» (Н. Бор)

Что в порядок ум она приводит,

Часто говорят о ней в народе.

Для победы трудностей закалку,

Развивать и волю и смекалку.

II. Актуализация знаний . Устный опрос.

У: На сегодняшнем уроке вы познакомитесь с еще одним способом решения комбинаторных задач. А его название вы мне потом скажете сами. Сегодня мы с вами будем решать задачи на изученные правила по комбинаторике, выполним лабораторную работу, а также творческую.

III. Открытие новых знаний

Решим задачу на странице 41 учебника. (Сколькими способами можно выбрать два различных цветка, если есть васильки, маки, ромашки и тюльпаны? Сколько получится пар, если их можно составлять и из двух одинаковых цветков?). Разобрать задачу устно, а затем приступить к ее оформлению и решению.

У: Начало задачи я предлагаю вам обозначить звездочкой «*» (учащиеся решают задачу под руководством учителя)

М Р Т В М Р Т В М Р Т В М Р Т В

Ответ: 12 способов без повторений, 16 способов с повторениями.

У: На что похожа данная схема? ( ученики высказывают свои версии названия) . Как звучит тема урока? (дерево возможных вариантов). Какую цель ставим перед собой? (научиться решать комбинаторные задачи с помощью перебора всех возможных вариантов) .

Часто процесс перебора удобно осуществлять путем построения специальной схемы – так называемого дерева возможных вариантов. Это название принято потому что, такая схема, как вы увидели, действительно напоминает дерево, правда расположенное «вверх ногами» и без ствола, только с «веточками».

IV . Закрепление и коррекция (практикум) .

У: А сейчас вы выполните лабораторную работу (см. приложение №1) . Задания о цифровых кодах. У вас на каждой парте лежит листок с заданиями, которые вы должны выполнить в парах . (учащиеся работают в парах).

У: Запишите в отдельной графе, чему вы научились в ходе выполнения данной лабораторной работы.

А теперь всем детям встать,

Пальцы сжать, потом разжать,

Наклон назад, наклон вперед.

Я вам раздам цветные полоски: белую, синюю и красную. Составьте их них флаг Российской Федерации.

-Что означает каждый цвет нашего флага? ( белый – мир, чистота, совершенство; синий – цвет веры и верности; красный – энергия, сила, кровь, пролитую за Отечество.)

Решение этой задачи можно записать двумя способами :

VI I . Рефлексия «Все в твоих руках». Итог урока .

— Чему вы научились на этом уроке?

— Что больше всего вам понравилось?

— Добились ли поставленной цели в начале урока? (Учащиеся сами оценивают работу одноклассников, аргументируя свое мнение) .

Домашнее задание. У.: стр. 38-39 читать, решить № 117, № 121.

Чтобы успешно выполнить домашнее задание вам необходимо будет внимательно прочитать теоретический материал в учебнике.

А как вы работали на уроке вы определите сами. (встают те учащиеся, которые хорошо работали на уроке. Остальные выставляют им отметки, аргументируя свое мнение).

Лабораторная работа по теме: Дерево возможных вариантов.

1. Чтобы выбрать первую цифру кода, у вас есть три варианта: цифры 1, 2 или 3. Поэтому от корня дерева проведите три ветви и на их концах поставьте цифры 1, 2 и 3.

1. Для выбора второй цифры кода есть те же три варианта: цифры 1, 2 и 3. Поэтому от каждой первой цифры кода проведите снова по три отрезка и на их концах опять запишите цифры 1, 2 и 3.

Место для выполнение работы.

Источник

конспект открытого урока математики в 5 классе по теме «Дерево возможных вариантов»
методическая разработка по алгебре (5 класс) по теме

Математику многие любят за ее вечные истины. Но реальная жизнь не так проста и однозначна. Исходы многих явлений предсказать невозможно, какой бы полной информацией мы не обладали. Такие закономерности изучает специальный раздел математики «Комбинаторика и теория вероятностей», который вводится, начиная с 5 класса. В данной разработке представлен конспект урока по теме «Дерево возможных вариантов», цель которого познакомить учащихся с основными приемами подсчета различных вариантов при решении комбинаторных задач.

Скачать:

Предварительный просмотр:

Конспект урока математики в 5 классе

Учитель математики МБОУ СОШ № 1 Слюнко О.В.

Тема: Дерево возможных вариантов.

Цель: познакомить учащихся с основными приёмами подсчета различных вариантов при решении комбинаторных задач.

· развивать логическое мышление, память, внимание, умение сравнивать и обобщать;

· воспитание интереса к предмету, культуры умственного труда.

ПК или ноутбук, проектор, экран.

Программное обеспечение: ОС Windows, MS Power Point, презентация к уроку.

II. Объяснение нового материала

В старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора (Слайд 2)

Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации. И целый раздел математики, именуемый комбинаторикой, занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.

Люди, которые владеют техникой решения комбинаторных задач, а, следовательно, обладают хорошей логикой, умением рассуждать, перебирать различные варианты решений, очень часто находят выходы, казалось бы, из самых трудных безвыходных ситуаций. Примером мог бы послужить сказочный герой Барон Мюнхгаузен, который находил выход из любой сложной и трудной ситуации. В жизни эти умения очень часто помогают человеку. Ведь в повседневной жизни нередко перед нами возникают проблемы, которые имеют не одно, а несколько различных вариантов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо осуществить перебор всех возможных вариантов или хотя бы подсчитать их число. Такого рода задачи называют комбинаторными.

Комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Задачей комбинаторики можно считать задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Сегодня рассмотрим с вами некоторые задачи комбинаторики. Мы научимся определять ход их решения, а также познакомимся и научимся применять на практике несколько методов решения комбинаторных задач.

Эти методы носят следующие названия: метод перебора, дерево возможных вариантов.

Задача 1. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? (Слайд 3)

Решение. Для того чтобы не пропустить и не повторить ни одно из чисел, будем выписывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4 и, наконец, с цифры 7. Получаем следующий расклад.

Источник

Комбинаторные задачи

Комбинаторика (от латинского слова combinare, означающего №соединять», «сочетать») — это область математики, которая изучает способы выбора, расположения, сочетания различных объектов. Решение задач в данном разделе математики требует рассмотрения и подсчёта всех возможных комбинаций (отсюда название комбинаторные задачи). Решая эти задачи, обычно надо отвечать на вопрос «Сколькими способами. » или «Сколько вариантов. «

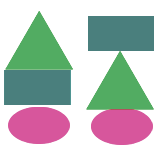
Задача: Нам даны фигуры: треугольник, овал и прямоугольник . Необходимо построить пирамидку, состоящую из трех разных фигур. Сколькими способами это можно сделать?

Метод перебора

Данный метод удобен при небольшом числе вариантов. Решение в данном случае происходит путём перебора всех возможных вариантов. При этом очень важно выбрать правильный вариант перебора — логику перебора.

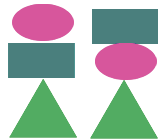
Воспользуемся методом перебора: Пусть в основании пирамидки находится прямоугольник, тогда возможны варианты построения: прямоугольник — овал — треугольник и прямоугольник — треугольник — овал.

Теперь в основании положим овал, тогда возможны варианты построения: овал — прямоугольник — треугольник и овал — треугольник — прямоугольник.

Теперь в основании положим треугольник, тогда возможны варианты построения: треугольник — прямоугольник — овал и треугольник — овал — прямоугольник.

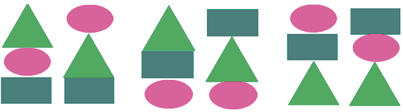
Итак, мы получили шесть возможных вариантов:

Ответ: 6 способов.

При решении данной задачи мы изображали фигуры, но для упрощения решения можно использовать кодирование. Данный прием позволяет заметить фигуры, например, первыми буквами их названия, то есть овал обозначаем буквой О, треугольник — Т, прямоугольник — П. Тогда решение будет выглядеть так:

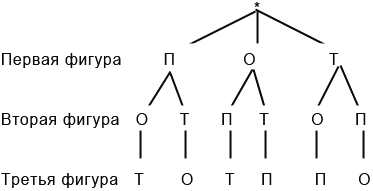
Дерево возможных вариантов

Данный метод заключается в построении схемы, которая и называется деревом возможных вариантов. Данная схема действительно похожа на перевернутое дерево, «корень» которого обозначается «*». Построим данную схему для нашей задачи: Для этого от «корня» проведем три «ветки» — отрезки, на концах которых подпишем варианты фигур, которые мы можем взять за основание. Далее от каждой фигуры проводим такое количество «веток», которое будет соответствовать числу вариантов фигур на втором месте, в нашем случае по две «ветки» от каждой фигуры. Затем от каждой фигуры, стоящей на втором месте, проводим такое число «веток», которое будет соответствовать числу вариантов фигур на третьем месте, в нашем случае по одной «ветке» от каждой фигуры. Тогда имеем следующее дерево возможных вариантов:

Метод отрезков

Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:

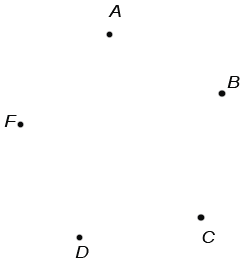
Необходимо ответить на вопрос: » Сколько отрезков изображено на рисунке?». Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:

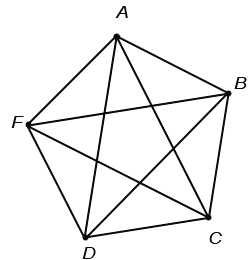
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:

Итак, мы получили 10 отрезков, соединяющих точки.

Ответ: На рисунке 10 отрезков.

Источник