Дерево является частным случаем

3-й семестр / Лекция 1 — Нелинейные структуры данных

function Parent(n:TNode;const T:Ttree):Tlabel; function Root(n:Tlabel;const T:Ttree):TNode; function Empty(T:TNodeR):Boolean; Procedure PreOrder(n:Tlabel;const T:Ttree); implementation Procedure CreateT(var T:Ttree); var i,w:integer; begin T.Root:=1; writeln(‘countNodes=’); readln(T.countNodes); for i:=1 to MaxNodes do //обнуление дерева begin T.Sons[i].Node:=’ ‘; T.Sons[i].Left:=0; T.Sons[i].Right:=0 end; for i:=1 to T.countNodes do begin writeln(‘Koren — Metka uzla char ‘, i); readln(T.Sons[i].Node); end; for i:=1 to T.countNodes do begin writeln(‘Left uzla ‘,T.Sons[i].Node); readln(T.Sons[i].Left); writeln(‘right uzla’); readln(T.Sons[i].right); end; end; function LeftSon(n:TNode;const T:Ttree):Tlabel; var i:integer; begin i:=1; while (i<= T.countNodes) and (T.Sons[i].Node<>n) do inc(i); if i>T.countNodes then LeftSon:= 0 else LeftSon:= T.Sons[i].left;

end; function rightBrather(n:TNode;const T:Ttree):Tlabel; var i:integer; begin i:=1; while (i<= T.countNodes) and (T.Sons[i].Node<>n) do inc(i); if i>T.countNodes then rightBrather:= 0 else rightBrather:= T.Sons[i].right; end; function Parent(n:TNode;const T:Ttree):Tlabel; var i:integer; begin //найти индекс узла n i:=1; while (i<= T.countNodes) and (T.Sons[i].Node<>n) do inc(i); if i>T.countNodes then result:= 0 else begin //если узел найден то //искать индекс в списке индексов левых сыновей result:=i; i:=1; while (i<= T.countNodes) and (T.Sons[i].left<>result) do inc(i); if i>T.countNodes then begin //поиск индекса в списке правых братьев i:=1; while (i<= T.countNodes) and (T.Sons[i].right<>result) do inc(i); if i>T.countNodes then result:=0 else

result:=i; end else result:=i; end; end; function Root(n:Tlabel;const T:Ttree):TNode; begin result:=T.Sons[n].Node; end; function Empty(T:TNodeR):Boolean; begin result:=T.Node=’ ‘; end; Procedure PreOrder(n:Tlabel;const T:Ttree); Var L,R:Tlabel; Begin If (n<>0)and not Empty(T.Sons[n]) then begin writeln(Root(n,T)); //можно заменить функцией обработки данных узла L:= LeftSon(root(n,T),T); PreOrder(L,T); While (L<>0) and (not Empty(T.Sons[L])) do Begin R:=rightBrather(Root(L,T),T); PreOrder(R,T); End; End End; end. Тестирующая программа для дерева рисунка 8. program Project2;

uses SysUtils, Unit1 in ‘Unit1.pas’; var T:Ttree; w:Tlabel; begin CreateT(T); w:=rightBrather(‘B’,T); writeln(w); preorder(T.Root,T); readln; end.

Источник

Ста: Лекция №7 — Деревья

Дерево — это математическая абстракция, состоящая из совокупности вершин, называемых узлами, и соединяющих их дуг, называемых ребрами, при этом существует не более одного ребра, соединяющего любую пару узлов, и отсутствуют циклы.

Дерево является частным случаем понятия графа, и имеет широкое распространение в дискретной математике и информатике. В практических задачах часто встречаются древовидные структуры, например:

• каталоги и файлы на диске;
• разделы и главы в книге;
• факультеты и кафедры в университете;
• области и районы в государстве.

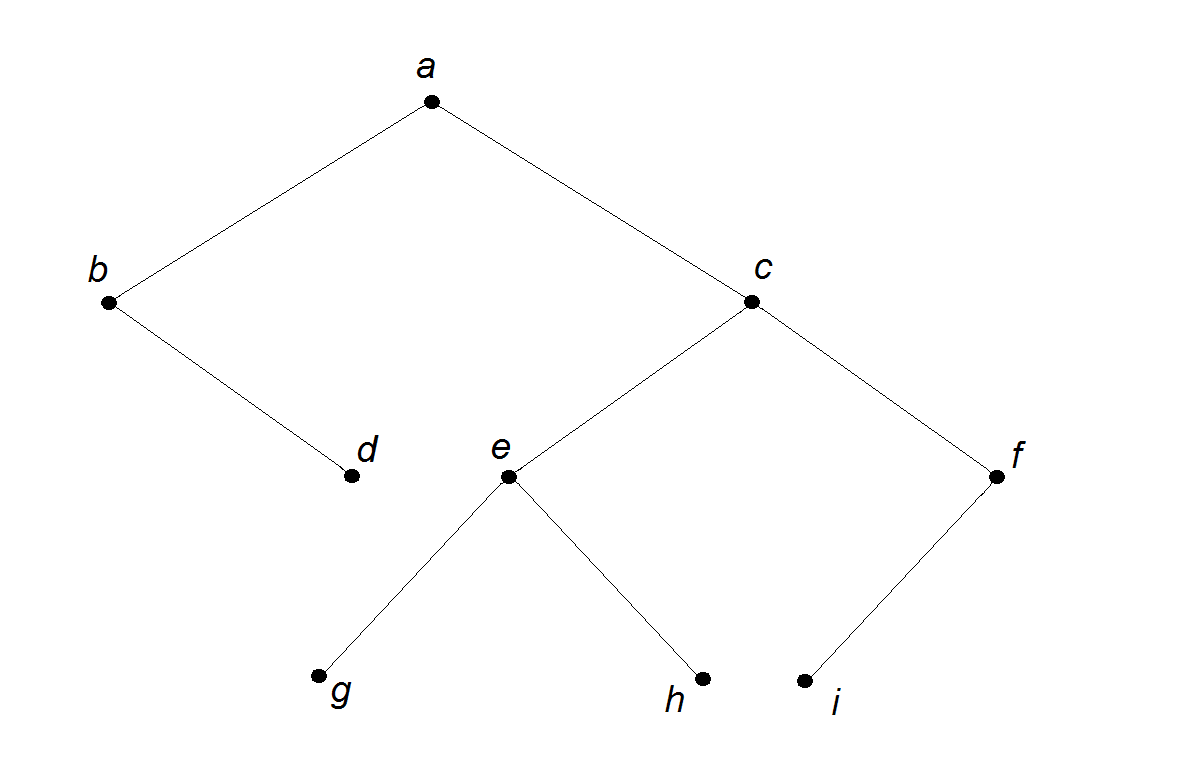
Пустое дерево — дерево, не содержащее ни одной вершины. Каждый узел дерева имеет не более одного узла-родителя и может иметь несколько узлов-потомков, или дочерних узлов. В приведенном ниже примере для узлов B, C и D узел A является родителем, а они для него — потомками. В свою очередь потомками узла B являются узлы E и F, для которых узел B является родителем. Узел G является потомком узла C, для него узел C является родителем. Корень дерева — это узел верхнего уровня, не являющийся потомком ни одного из других узлов. У непустого дерева может быть только один корень. В данном примере корнем является узел A. Узлы, не имеющие потомков, называются листьями. В приведенном примере листьями являются узлы D, E, F и G. Узлы-потомки, обладающие общим узлом-родителем, называются братскими. В данном примере братскими между собой являются узлы B, C, D (общий родитель — узел A), узлы E и F (общий родитель — узел B). Совокупность узлов и соединяющих их ребер, начинающаяся от узла-потомка с точки зрения родителя, называется поддеревом. Например, с точки зрения узла A имеется 3 поддерева:

• поддерево, состоящее из узлов B, E, F
• поддерево, состоящее из улов C и G
• поддерево, состоящее из единственного узла D.

Путем в дереве называется последовательность ребер, соединяющая два связанных узла. Существует не более одного пути между любыми двумя узлами дерева (0 либо 1). Для любого некорневого узла всегда существует путь до корня. Длина пути от некоторого выбранного узла до корневого, т.е. количество участвующих в пути узлов, называется высотой узла. В частности, высота узла A равна 1, высота узлов B, C и D равна 2, а высота узлов E, F и G равна 3. Наибольшая высота соответствует наиболее отдаленным от корня узлам-листам, и называется высотой дерева. В примере наибольшая высота узла равна 3, отсюда высота дерева также равна 3. Дерево, у которого среди всех нелистовых узлов имеется не более N потомков на один узел-родитель, называется N-арным деревом. В таком дереве допускается, что каждый узел имеет от 0 до N узлов-потомков. Приведенный пример представляет собой N-арное дерево с кратностью 3, поскольку наиболее разветвленный узел A имеет 3 узла-потомка. Если для каждого узла-родителя имеет значение порядок перечисления соответствующих ему узлов-потомков, такое дерево называется упорядоченным. В противном случае, когда порядок перечисления дочерних узлов может быть любым, дерево является неупорядоченным. Особый случай представляют собой бинарные, или двоичные, деревья. Бинарное дерево — это частный случай упорядоченного N-арного дерева, у которого N=2. Для каждого узла-родителя бинарного дерева поддеревья, образуемые первым и вторым узлами, называются левым и правым поддеревом соответственно. Также как для элементов связных списков, с узлами деревьев могут быть ассоциированы произвольные данные-значения, иногда в литературе называемые метками узлов.

Источник

2.5.2. Бинарные деревья

Бинарным деревом называется дерево, каждый узел которого имеет не более двух поддеревьев (равносильное условие: если из каждого узла — при общепринятой ориентации сверху от корня вниз к листьям — выходят не более двух дуг). Одно из этих поддеревьев считается левым, а другое правым (любое из них может отсутствовать).

Особая важность бинарных деревьев связана с тем, что данные со структурой дерева общего типа могут быть представлены в памяти компьютера в виде эквивалентного бинарного дерева.

Рекурсивное определение бинарного дерева: это пустое дерево, либо корень с двумя бинарными деревьями. Бинарное дерево может быть пустым

Частным случаем бинарного дерева является —дерево (или строго бинарное дерево), каждый узел которого является либо корнем точно двух поддеревьев, либо является листом (рис. 14). Количество узлов -дерева нечётно.

Между бинарными деревьями с узлами и-деревьями сузлами можно установить взаимно однозначное соответствие следующим образом. Ко всем концевым узлам бинарного дереваприсоединим-дерево с тем же корнем и двумя помеченными узлами ■; ко всем не концевым узлам с одним потомком присоединим ещё одного потомка в виде помеченного узла. В результате бинарное дерево перейдёт в-дерево, все концевые узлы которого помечены. Обратно, удаляя все концевые узлы-дерева, получим бинарное дерево(рис. 15).

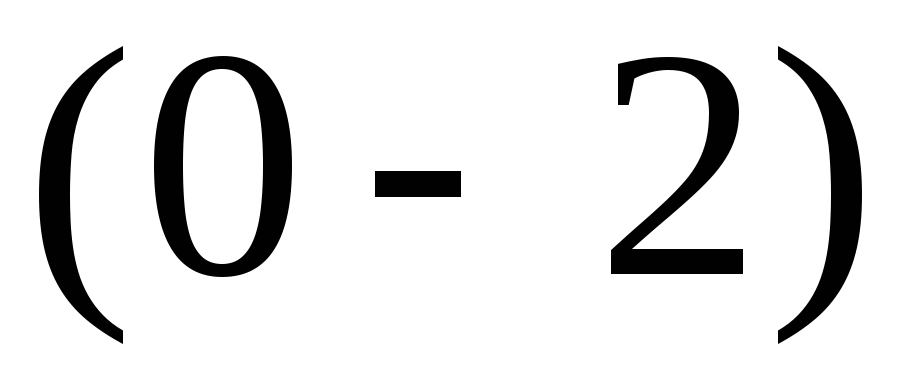
Ещё один частный случай бинарного дерева — полное бинарное дерево. В таком дереве каждый узел, не являющийся листом, имеет степень (имеет два поддерева) и все листья имеют один и

тот же уровень . Числов этом случае называется уровнем полного бинарного дерева. В полном бинарном дереве количество узловравно сумме геометрической прогрессии:

.

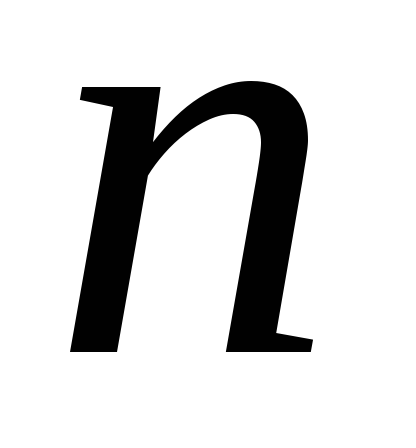
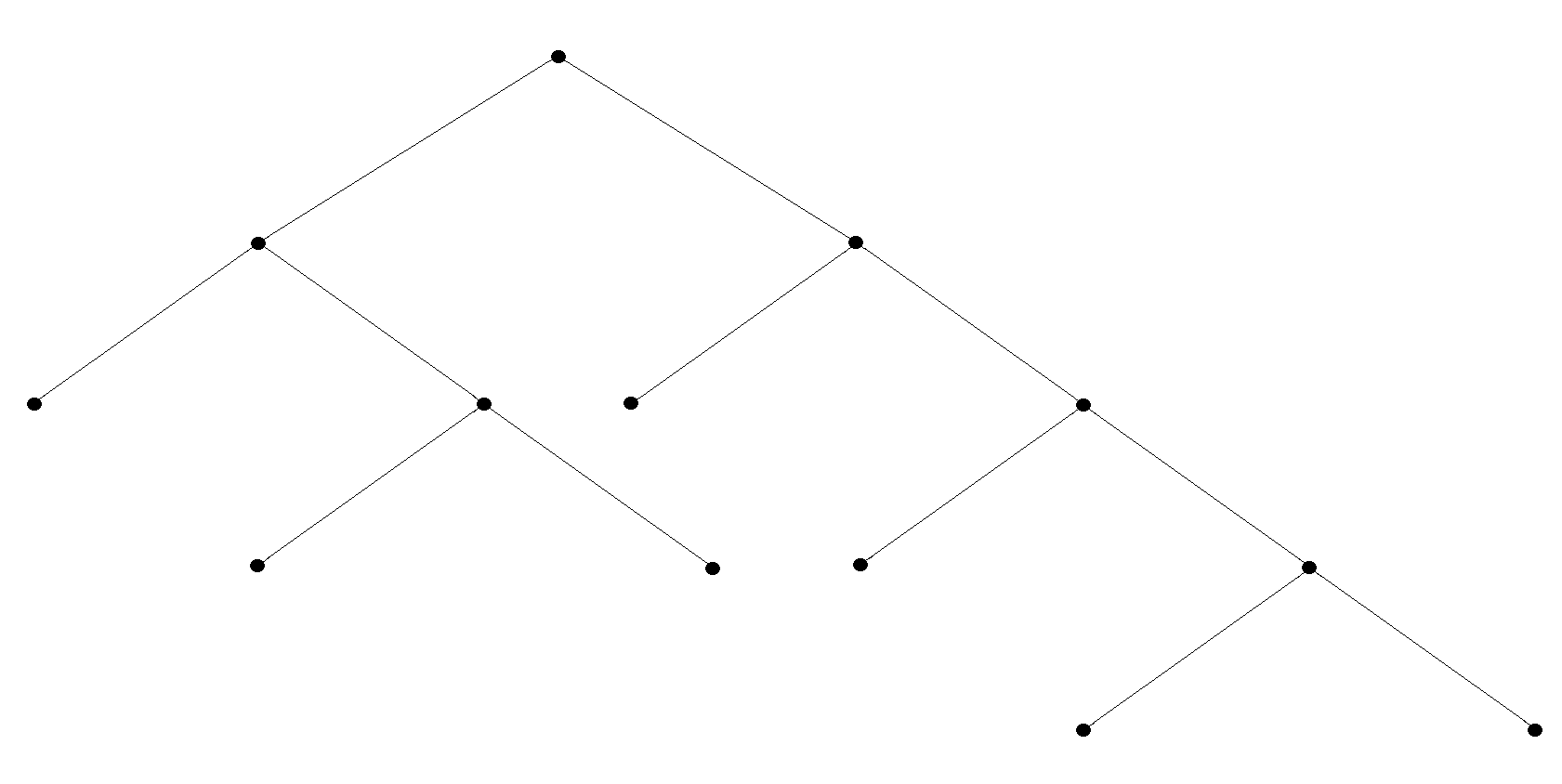
На (рис. 16) изображено полное бинарное дерево уровня .

С рекурсивным определением бинарных деревьев связан естественный способ их представления в памяти компьютера в виде цепных списков или в виде массивов.

Представление бинарных деревьев цепным списком. Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент наряду с полем данных имеет два поля указателей. Один указатель используется для связывания элемента с левым потомком, а другой с правым. Листья имеют пустые указатели потомков. При таком способе представления обязательно следует сохранять указатель на узел, являющийся корнем всего дерева.

Итак, для представления бинарного дерева вводится указатель на дерево (адрес корня), и в каждый узел помимо поля значениявключаются ещё два поляи(рис. 17) для цепной адресации с двумя узлами следующего уровня — левым и правым, которые являются корнями соответствующих поддеревьев; в случае отсутствия одного из них или обоих в эти поля помещается соответствующий признак. Указатель пустого дерева.

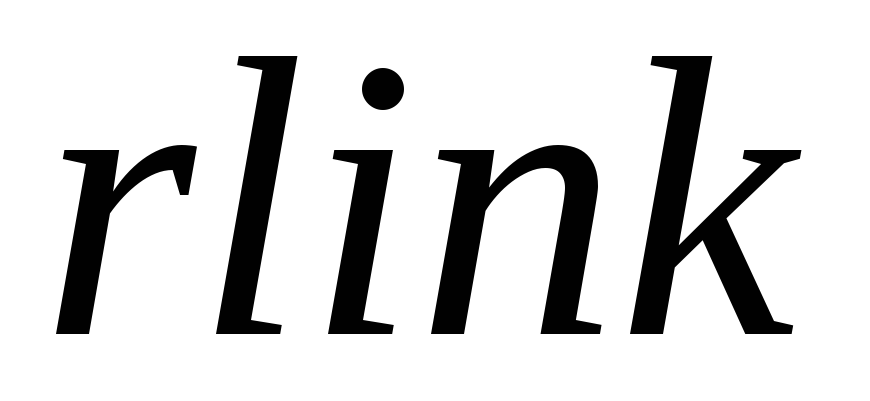
Пример. Дерево, изображённое на рис. 18, имеет в памяти представление, приведённое на рис. 19.

Представление бинарных деревьев массивом. В виде одномерного массива проще всего представляется полное бинарное дерево, так как оно всегда имеет строго определенное число узлов на каждом уровне. Узлы можно естественным образом упорядочить, нумеруя слева направо последовательно по уровням и использовать эти номера в качестве индексов в одномерном массиве (рис. 20).

Если есть основания предполагать, что число уровней дерева в процессе работы с ним не будет значительно меняться, то данный способ представления полного бинарного дерева значительно более экономичен, чем представление списковой структурой.

Для представления неполных бинарных деревьев можно применить следующий способ:

1. Бинарное дерево дополняется до полного дерева, вершины последовательно нумеруются.

2. В массив заносятся поля данных только тех узлов, которые были в исходном неполном дереве, в соответствии с индексами этих узлов в полном дереве.

3. В незанятые элементы массива заносится характерное значение в качестве признака пропуска элемента.

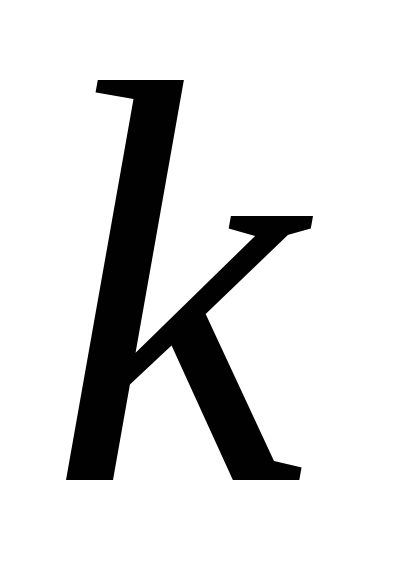
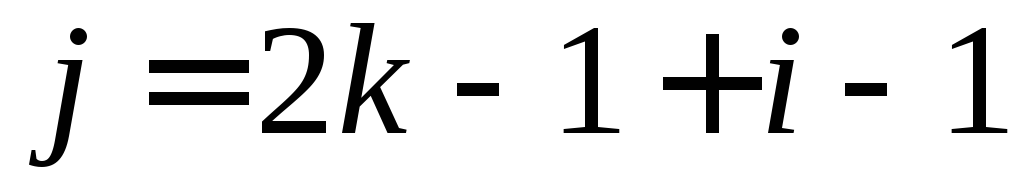
Если узел имеет в дереве уровень и занимает среди узлов этого уровня позицию с номером, то для его индекса в представляющем массиве справедлива формула:. Индекс корня оказывается равен единице. Для любого узла с координатами в деревеиндексыиего левого и правого потомков вычисляются по формулам:

; .

Главным недостатком рассмотренного способа представления бинарного дерева является то, что структура данных является статической. Размер массива выбирается исходя из максимально возможного количества уровней бинарного дерева. При этом, чем менее полным является дерево, тем менее рационально используется память.

Источник