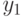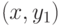Теория графов – деревья
Деревья – это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
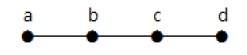
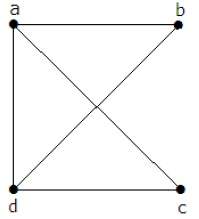
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
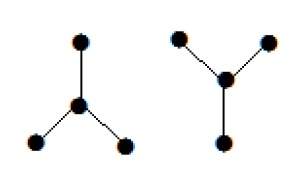
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
Охватывающие деревья
Пусть G – связный граф, тогда подграф H в G называется остовным деревом в G, если –
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
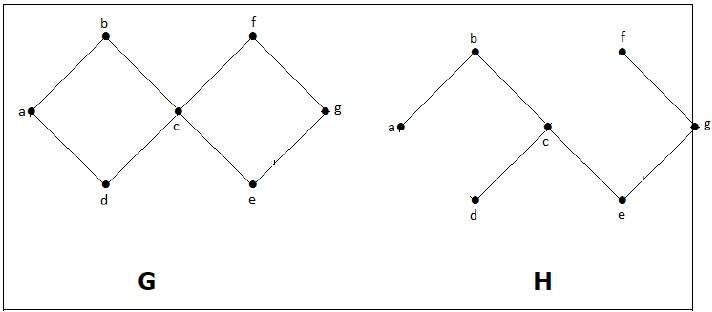
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H – остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
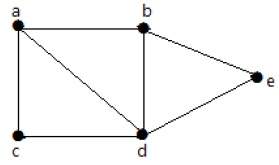
Посмотрите на следующий график –
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
пример
Пусть ‘G’ – связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
Дерево, эквивалентные определения
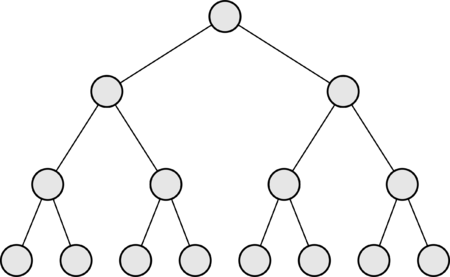
Для графа [math]G[/math] эквивалентны следующие утверждения:
- [math]G[/math] — дерево.
- Любые две вершины графа [math]G[/math] соединены единственным простым путем.
- [math]G[/math] — связен и [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
- [math]G[/math] — ацикличен и [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер.
- [math]G[/math] — ацикличен и при добавлении любого ребра для несмежных вершин появляется один простой цикл.
- [math]G[/math] — связный граф, отличный от [math] K_p [/math] для [math] p \gt 3 [/math] , а также при добавлении любого ребра для несмежных вершин появляется один простой цикл.
- [math]G[/math] — граф, отличный от [math] K_3 \cup K_1 [/math] и [math] K_3 \cup K_2 [/math] , а также [math] p = q + 1 [/math] , где [math]p[/math] — количество вершин, а [math]q[/math] количество ребер, и при добавлении любого ребра для несмежных вершин появляется один простой цикл.
Доказательство эквивалентности
Граф связен, поэтому любые две вершнины соединены путем. Граф ацикличен, значит путь единственен, а также прост, поскольку никакой путь не может зайти в одну вершину два раза, потому что это противоречит ацикличности.
Очевидно, что граф связен. Докажем по индукции, соотношение [math]p = q + 1[/math] . Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше [math]p[/math] вершин. Если же граф [math]G[/math] имеет [math]p[/math] вершин, то удаление из него любого ребра делает граф [math] G [/math] несвязным в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин на единицу больше числа ребер. Таким образом, [math] p = q + 1 [/math] .
Очевидно, что если граф связен и ребер на одно меньше, чем вершин, то он ацикличен. Преположим, что у нас есть p вершин, и мы добавляем ребра. Если мы добавили ребро для получения цикла, то добавили второй путь между парой вершин, а значит нам не хватит его на добавление вершины и мы получим не связный граф, что противоречит условию.
[math]G[/math] — ациклический граф, значит каждая компонента связности графа является деревом. Так как в каждой из них вершин на единицу больше чем ребер, то [math] p = q + k [/math] , где [math]k[/math] — число компонент связности. Поскольку [math] p = q + k [/math] , то [math] k = 1 [/math] , а значит [math]G[/math] — связен. Таким образом наш граф — дерево, у которого между любой парой вершин есть единственный простой путь. Очевидно, при добавлении ребра появится второй путь между парой вершин, то есть мы получим цикл.
Поскольку [math] K_p [/math] для [math] p \gt 3 [/math] содержит простой цикл, то [math]G[/math] не может им являться. [math]G[/math] связен, так как в ином случае можно было бы добавить ребро так, что граф остался бы ациклическим.
Докажем, что любые две вершины графа соединены единственной простой цепью, а тогда поскольку [math] 2 \Rightarrow 3 [/math] , получим [math] p = q + 1 [/math] . Любые две вершины соединены простой цепью, так как [math]G[/math] — связен. Если две вершины соединены более чем одной простой цепью, то мы получим цикл. Причем он должен являться [math] K_3 [/math] , так как иначе добавив ребро, соединяющее две вершины цикла, мы получим более одного простого цикла, что противоречит условию. [math] K_3 [/math] является собственным подграфом [math]G[/math] , поскольку [math]G[/math] не является [math] K_p [/math] для [math] p \gt 3 [/math] . [math]G[/math] — связен, а значит есть вершина смежная с [math] K_3 [/math] . Очевидно, можно добавить ребро так, что образуется более одного простого цикла. Если нельзя добавить ребра так, чтобы не нарушалось исходное условие, то граф [math]G[/math] является [math]K_p[/math] для [math] p \gt 3 [/math] , и мы получаем противоречие с исходным условием. Значит, любые две вершины графа соединены единственной простой цепью, что и требовалось.
Если [math]G[/math] имеет простой цикл, то он является отдельной компонентой [math]K_3[/math] по ранее доказанному. Все остальные компоненты должны быть деревьями, но для выполнения соотношения [math] p = q + 1 [/math] должно быть не более одной компоненты отличной от [math]K_3[/math] , так как в [math]K_3[/math] [math] p = q = 3 [/math] . Если это дерево содержит простой путь длины 2, то в [math]G[/math] можно добавить ребро так, что образуются два простых цикла. Следовательно, этим деревом является [math]K_1[/math] или [math]K_2[/math] . Значит [math]G[/math] является [math]K_3 \cup K_1[/math] или [math]K_3 \cup K_2[/math] , которые мы исключили из рассмотрения. Значит наш граф ацикличен. Если [math]G[/math] ациклический и [math] p = q + 1 [/math] , то из [math] 4 \Rightarrow 5 [/math] и [math] 5 \Rightarrow 6 [/math] верно, что [math]G[/math] — связен. В итоге получаем, что [math]G[/math] является деревом по определению.
См. также
Источники информации
- Харари Ф. Теория графов. /пер. с англ. — изд. 2-е — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Википедия — дерево(теория графов)
Источник
Важнейшие классы графов
Деревом называется связный граф , не имеющий циклов. В графе без циклов, таким образом, каждая компонента связности является деревом. Такой граф называют лесом .
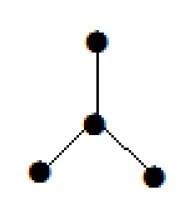
 ребрами является деревом тогда и только тогда, когда он удовлетворяет любым двум из следующих трех условий:
ребрами является деревом тогда и только тогда, когда он удовлетворяет любым двум из следующих трех условий:
 (3). Индукция по числу вершин. При
(3). Индукция по числу вершин. При 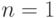 утверждение очевидно. При
утверждение очевидно. При  в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность, очевидно, сохранится. В этом новом дереве
в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность, очевидно, сохранится. В этом новом дереве  вершин и, по предположению индукции,
вершин и, по предположению индукции,  ребра. Следовательно, в исходном дереве было
ребра. Следовательно, в исходном дереве было