Деревья четыре вершины граф

Теория графов – деревья

Деревья – это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.

Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.

дерево

Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.

Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .

Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.

Пример 1

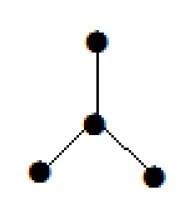
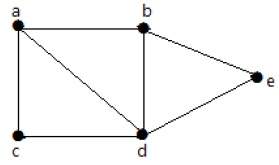
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.

Примечание. Каждое дерево имеет как минимум две вершины первой степени.

Пример 2

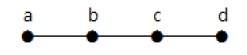
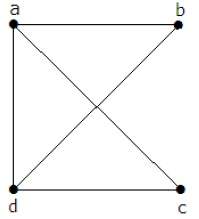
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.

лес

Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.

пример

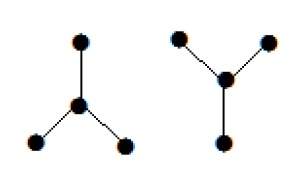
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.

Охватывающие деревья

Пусть G – связный граф, тогда подграф H в G называется остовным деревом в G, если –

Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.

пример

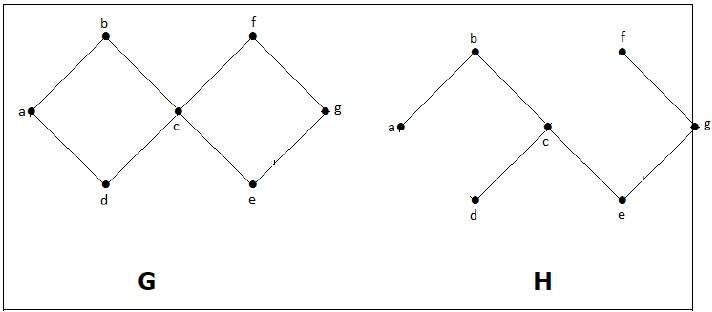
В приведенном выше примере G является связным графом, а H является подграфом G.

Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H – остовное дерево группы G.

Circuit Rank

Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.

Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.

Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.

Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.

пример

Посмотрите на следующий график –

Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.

пример

Пусть ‘G’ – связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».

По сумме теоремы о степени вершин

Теорема Кирхгофа

Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.

пример

Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».

Источник

§ 3.2. Деревья и леса

Дерево – связный граф без циклов. Лес – произвольный граф без циклов.

Очевидно, связные компоненты леса являются деревьями. Необходимые и достаточные условия для графа “быть деревом” даёт следующая теорема.

Теорема. Связный граф является деревом в том и только том случае, если количества его вершин и рёбер связаны соотношением

Отметим ещё два свойства деревьев: 1) для любых вершин и дерева существует единственный путь из в 2) в любом дереве есть висячая вершина (если дерево имеет хотя бы одно ребро, то у него не менее двух висячих вершин).

Упражнение 3.12. Найти количество неизоморфных графов с 3 вершинами.

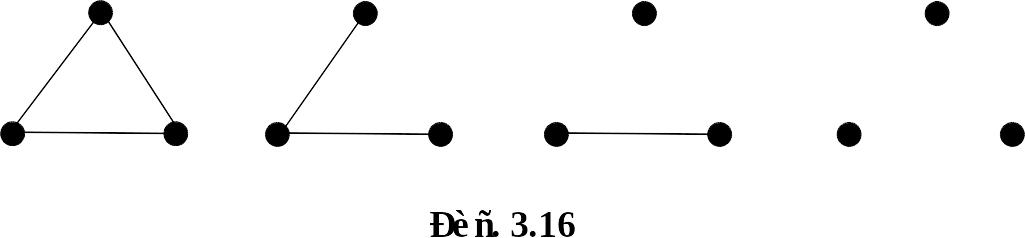
Решение. Если граф с 3 вершинами не имеет ни одного ребра, то он изоморфен Рассматривая далее случаи графов с 1, 2, 3 рёбрами, мы получим все неизоморфные графы с 3 вершинами – см. рис. 3.16. Их всего 4.

Упражнение 3.13. Найти все (с точностью до изоморфизма) связные графы с 4 вершинами.

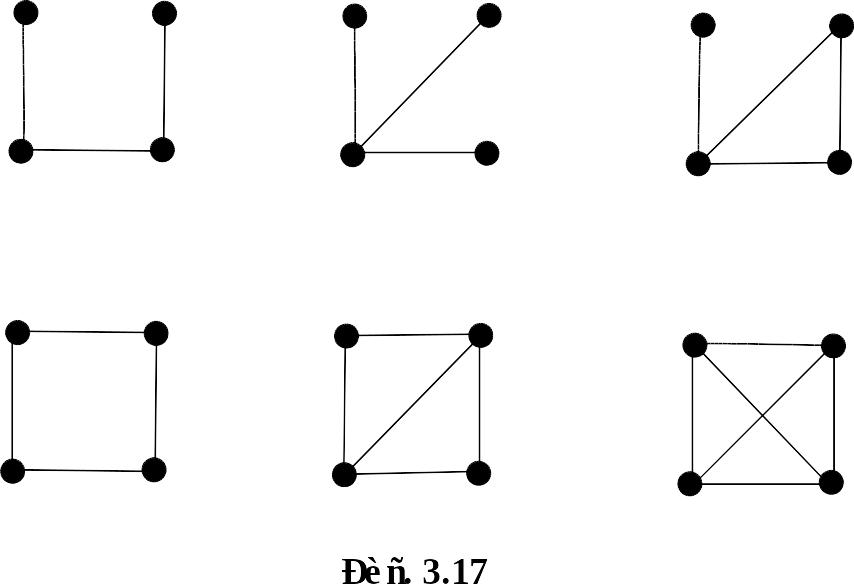
Р ешение. Пусть – граф с 4 вершинами. Понятно, что если рёбер два или меньше, то несвязен. Следовательно, возможное количество рёбер – это 3, 4, 5, 6. Граф с 6 рёбрами – полный, он изоморфен графу Несложный перебор оставшихся вариантов показывает, что графов, удовлетворяющих требуемым условиям, ровно 6. Они изображены на рис. 3.17.

Упражнение 3.14. Найти все (с точностью до изоморфизма) деревья с 5 вершинами.

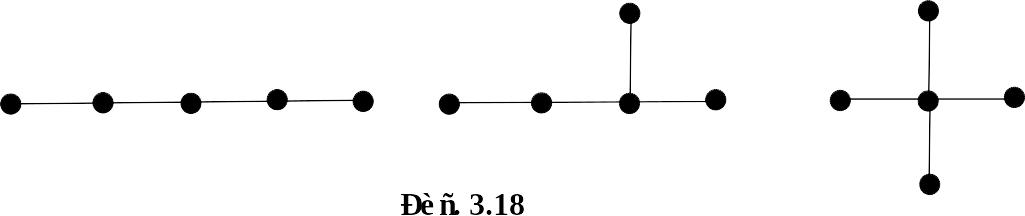
Решение. Пусть – дерево с 5 вершинами. Понятно, что возможны ровно 3 следующих случая: а) все степени вершин не превосходят 2; б) есть вершина степени 3; в) есть вершина степени 4. В каждом из этих случаев имеется по одному дереву – см. рисунок 3.18.

Существуют способы компактной записи (кодирования) деревьев. Из них мы рассмотрим два: двоичное (или бинарное) кодирование (т.е. составление кода из 0 и 1) и кодирование Прюфера (код из натуральных чисел).

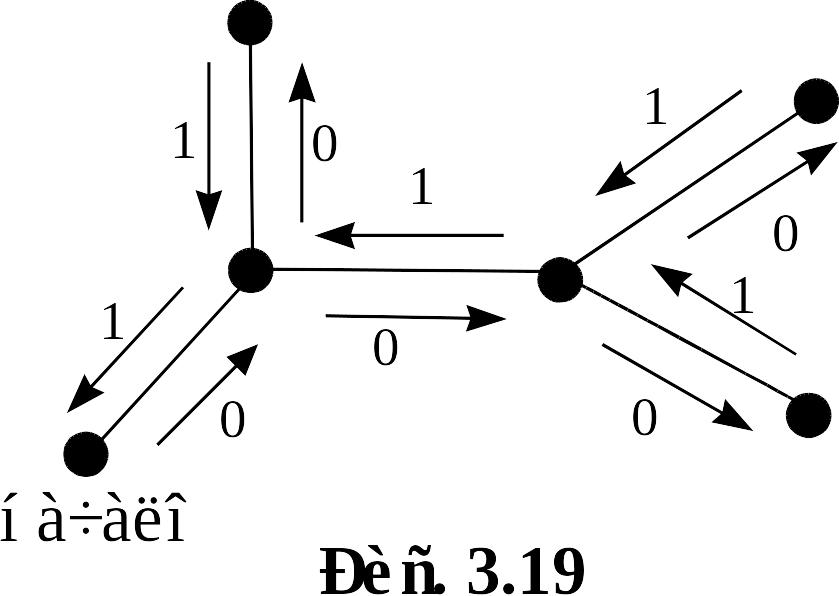
П ри бинарном кодировании каждому дереву приписывается последовательность из 0 и 1 длины где – количество рёбер дерева. В этой последовательности ровно единиц и столько же нулей. Для составления кода представим себе, что граф представляет собой реку, по берегу которой мы совершаем её обход так, чтобы река оставалась всё время с одной стороны, для определённости будем считать, что слева. При проходе по ребру в первый раз в код записывается 0, а второй раз (по противоположному берегу) – пишется 1. На рисунке 3.19 показано на примере, как осуществляется бинарное кодирование.

Двоичное кодирование дерева неоднозначно. Оно зависит от выбора начала обхода, направления обхода, а также изображения дерева на плоскости. Далее, не всякая последовательность из единиц и нулей является бинарным кодом какого-нибудь дерева. Необходимое и достаточное условие существования дерева для данной двоичной последовательности даёт следующее утверждение.

Теорема. Пусть – последовательность, в которой нулей и единиц. Она является бинарным кодом некоторого дерева в том и только том случае, если в любом её начальном отрезке количество нулей не меньше количества единиц.

Например, последовательность 0011011100011 не является кодом никакого дерева (так как содержит начальный отрезок 00110111), а последовательность 00011010011011 является кодом дерева.

Декодирование (т.е. построение дерева по коду) можно осуществить, копируя процесс кодирования, т.е. восстанавливая “реку”, обход которой был совершён.

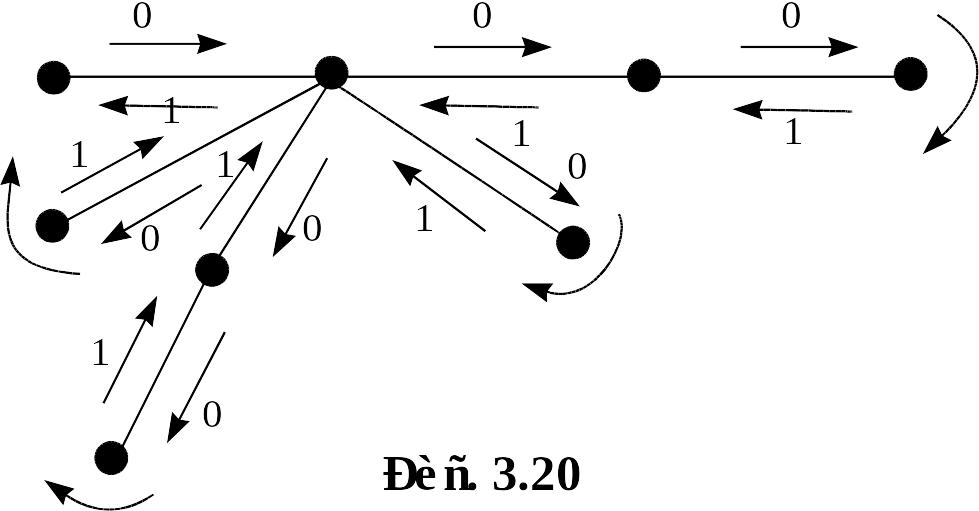
Упражнение 3.15. Построить дерево по его двоичному коду 00011010011011.

Решение показано на рисунке 3.20.

Для построения кода Прюфера вначале следует занумеровать вершины дерева натуральными числами (произвольным образом). Далее поступаем так. Берём висячую вершину с наименьшим номером. Пусть это будет вершина с номером Она инцидентна единственной вершине, которая имеет номер, скажем, Тогда записываем в код и удаляем вершину с ребром после чего возвращаемся к началу алгоритма. Это делается до тех пор, пока не останется одно ребро. Длина кода получается равной где – количество вершин дерева.

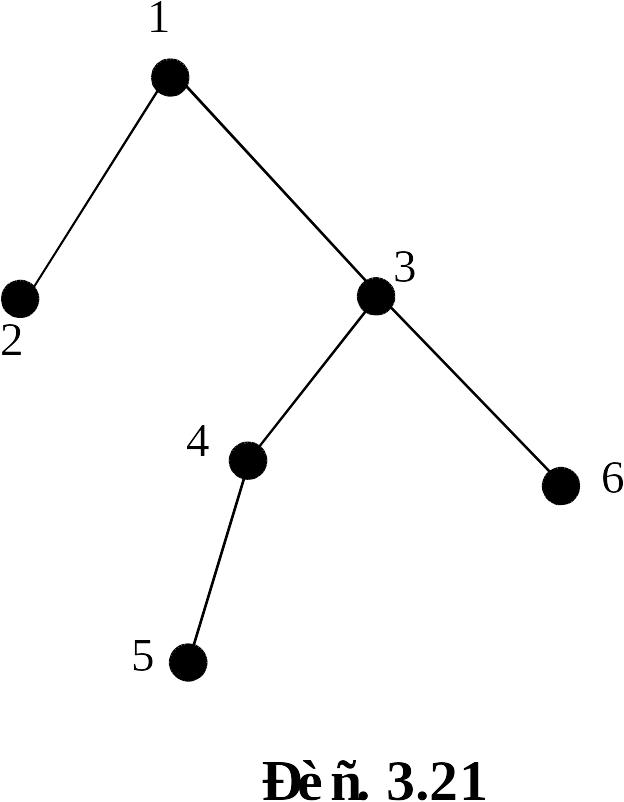
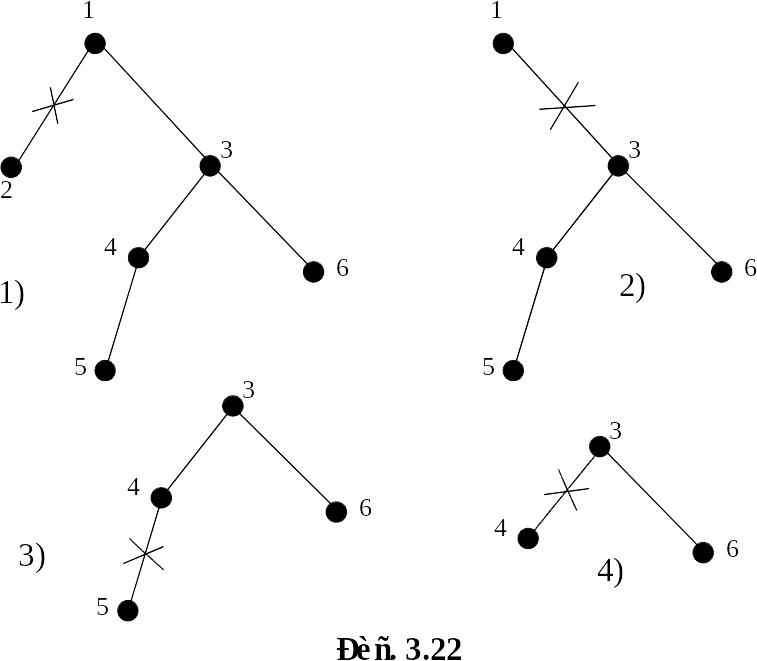
Упражнение 3.16. Построить код Прюфера дерева, изображённого на рисунке 3.21.

Р ешение. Применим описанный выше алгоритм (см. рисунок 3. 22):

1. висячая вершина с наименьшим номером – 2; пишем 1, удаляем вершину 2 и ребро (1,2);
2. висячая вершина – 1; пишем 3, удаляем вершину 1 и ребро (1,3);
3. висячая вершина – 5; пишем 4, удаляем вершину 5 и ребро (4,5);
4. висячая вершина – 4; пишем 3, удаляем вершину 4 и ребро (4,3).

Декодирование кода Прюфера осуществляется следующим образом. Пусть дан код где Нарисуем на плоскости точек, занумерованных числами пока не соединённые друг с другом рёбрами. Далее рисуем рёбра одно за другим согласно следующему правилу:

1. находим – наименьшее число из множества которого нет в последовательности соединяем ребром вершины и
2. находим – наименьшее число из множества не встречающееся в последовательности соединяем ребром вершины и
3. находим – наименьшее число из множества не встречающееся в последовательности соединяем ребром вершины и

находим – наименьшее число из множества не встречающееся в последовательности соединяем ребром вершины и

в последовательности отсутствуют ровно 2 числа из множества обозначим их и соединим соответствующие вершины.

Упражнение 3.17. Построить дерево по коду 1353.

Решение. Применим описанный выше алгоритм.

1. Так как длина кода равна 4, то дерево будет иметь 6 вершин. Нарисуем на плоскости точки 1,2,3,4,5,6.
2. Наименьшее число – это 2. Пишем его под 1:
3. Наименьшее число – это 1. Пишем его под 3:
4. Наименьшее число – это 4. Пишем его под 5:
5. Н аименьшее число – это 5. Пишем его под 3:
6. Отсутствуют в последовательности 2145 числа 3 и 6.

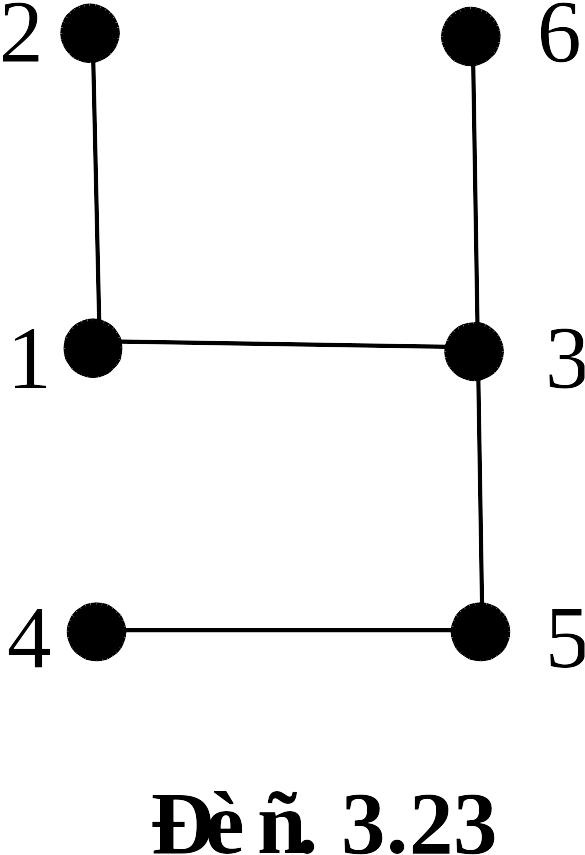
Таким образом, в графе будут следующие рёбра: (1,2), (3,1), (5,4), (3,5), (3,6). Искомое дерево изображено на рисунке 3.23.

Замечание. В отличие от бинарного кода код Прюфера определяется деревом однозначно, если зафиксирована нумерация вершин дерева. Назовём дерево с заданной на нём нумерацией вершин помеченным деревом. Кодирование Прюфера определяет взаимно однозначное соответствие между помеченными деревьями и их кодами. Следовательно, число помеченных деревьев с вершинами (обозначим это число ) равно числу их кодов. Кодом является произвольная последовательность чисел, взятых из множества Таким образом, мы имеем:

Формула (5) называется формулой Кэли.

Источник

13. Деревья

Рассмотрим граф , Имеющий P вершин и Q ребер.

Определение. Деревом называется связный граф без циклов.

Определение. Остовным деревом произвольного графа называется его Остовной подграф, являющийся Деревом.

Например, на рис. 20 представлено остовное дерево графа, диаграмма которого изображена на рис. 1.

Рис. 20. Остовное дерево графа

Всякое дерево является двудольным графом.

Теорема 23.

1) Граф является деревом тогда и только тогда, когда .

2) Граф является деревом тогда и только тогда, когда Любые Две его вершины соединены единственной Простой цепью.

Пример. Волейбольная сетка имеет вид прямоугольника, состоящего из клеток. Какое наибольшее число веревочек можно перерезать так, чтобы сетка не распалась?

Решение. Рассмотрим граф, соответствующий клетчатому полю M на N, M = 50, N = 600. Число вершин графа равно
= . Число ребер графа равно
= . Сетка не распадётся до тех пор, пока соответствующий ей граф с вершинами и рёбрами будет связным. По условию задачи , а уменьшается. Пока связный граф содержит циклы, можно, не нарушая связности, удалять любое ребро цикла. Процесс продолжается до тех пор, пока не получится связный граф без циклов, то есть дерево. Дерево с вершинами имеет рёбер. Значит, можно удалить верёвочек. □

Теорема 24. Число Различных деревьев, которые можно построить на P занумерованных вершинах непустого графа, имеющего не менее двух вершин, равно .

Например, число различных деревьев, которые можно построить на четырёх занумерованных вершинах графа, представленного на рис. 1, равно 16.

Определение. Лесом называется несвязный граф без циклов.

Каждая компонента связности леса является деревом.

Например, на рис. 21 представлена диаграмма леса, имеющего две компоненты связности.

Определение. Весом ребра Графа называется действительное число, поставленное в соответствие этому ребру по специальному правилу.

Такой граф называется нагруженным. Вес графа равен сумме весов его ребер.

Например, на рис. 22 представлены нагруженный граф и его остовное дерево наименьшего веса.

Рис. 22. Нагруженный граф и его остовное дерево наименьшего веса

54. Постройте диаграммы графов, заданных следующими матрицами смежности. Установите, являются ли эти графы деревьями.

1) ; 2) .

55. Дерево имеет три вершины степени 3 и четыре вершины степени 2. Остальные вершины дерева имеют степень 1. Сколько вершин дерева имеет степень 1?

56. Найдите все различные деревья графа .

57. Постройте диаграмму леса с семью вершинами и двумя компонентами связности. Найдите число его рёбер.

58. Найдите цикломатическое число дерева задачи 55.

59. В шахматном турнире по олимпийской системе участвуют 8 человек. Сколько всего встреч будет проведено?

Источник