- Теория графов – деревья
- дерево
- Пример 1
- Пример 2
- лес
- пример
- Охватывающие деревья
- пример
- Circuit Rank
- пример
- пример
- Теорема Кирхгофа
- пример
- 3 Покрывающие деревья (остовы)
- Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
- Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- Лекция 12 Двудольные и планарные графы
- 1 Двудольные графы
- 2. Экстремальное дерево графа
- Деревья покрытия. Остовы
- Раскраска графов
- Алгоритм правильной раскраски
Теория графов – деревья
Деревья – это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
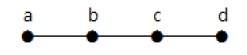
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
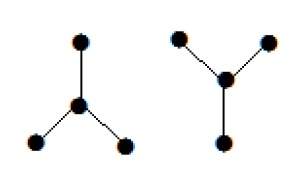
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
Охватывающие деревья
Пусть G – связный граф, тогда подграф H в G называется остовным деревом в G, если –
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
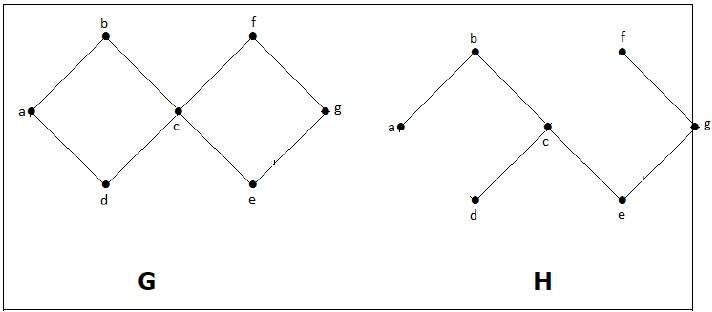
пример
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H – остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
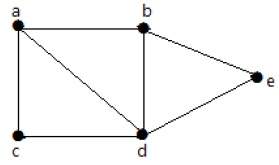
пример
Посмотрите на следующий график –
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
пример
Пусть ‘G’ – связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
3 Покрывающие деревья (остовы)
Цикломатическим числом неориентированного графа G называется величина γ(G) = т — п + k, где т — число ребер, п — число вершин, k — число связных компонент. Для дерева и леса γ (G) = 0, для других графов γ (G) > 0.
Остовом, или покрывающим деревом, связного графа G=(V, E) называется часть G, которая содержит все его вершины и является деревом. Хордой остова графа G называется ребро G, не принадлежащее остову.
Очевидно, что любой связный граф имеет хотя бы один остов, а любой несвязный граф остова не имеет.
В последующем алгоритме части исходного графа G, которые возникают в процессе построения покрывающего дерева, будем называть букетами.
Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g
1. Выбрать любое ребро G, не являющееся петлей. Пометить его меткой α и объявить букетом это ребро вместе с его концевыми вершинами.
2. Выбрать любое непомеченное ребро G, не являющееся петлей:
а) если один из концов выбранного ребра принадлежит построенному ранее букету В, а другой конец свободен (не принадлежит ни одному букету), пометить выбранное ребро меткой α, включить его вместе со свободным концом в букет В и перейти к шагу 3;
б) если оба конца выбранного ребра свободны, пометить его меткой а, объявить это ребро вместе с его концевыми вершинами новым букетом и перейти к шагу 3;
в) если концы выбранного ребра принадлежат разным построенным ранее букетам В и С, пометить выбранное ребро меткой α, включить его и букет С в букет В и перейти к шагу 3;
г) если оба конца выбранного ребра принадлежат одному букету, пометить его меткой β и перейти к шагу 3;
д) если непомеченных ребер нет, закончить алгоритм.
3. Если все вершины графа G вошли в один букет, закончить алгоритм. Если нет, перейти к шагу 2.
Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g
- Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G2 графа G. Положим i:=2.
- Если i=n(G), то задача решена и Gi – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).
- Строим граф Gi+1. Для этого добавим к графу Gi новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа Gi и одновременно вершине, не содержащейся в Gi. Вместе с этим ребром включаем в Gi+1 и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2.
Лекция 12 Двудольные и планарные графы
1 Двудольные графы
Двудольным графом G=(X, Y, Е) называется неориентированный граф, вершины которого можно разбить на два класса X и Y так, что концы каждого ребра принадлежат разным классам. Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли, полный двудольный граф принято обозначать символом 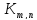
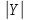
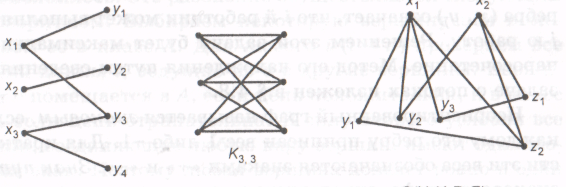
Источник
2. Экстремальное дерево графа
Определение 12.2. Конечный связный неориентированный граф без циклов называется деревом.
Примеры. На рисунке 12.7 представлены примеры деревьев:
Дерево, имеющее n вершин, включает в себя n–1 ребро. При составлении дерева используется минимальное число ребер, чтобы граф был связным. При включении в дерево любого дополнительного ребра возникнет цикл. Дерево может быть частью неориентированного графа. Любая совокупность ребер графа попарно связанных отношением смежности и инцидентности и соответствующие им вершины образует дерево графа. Если такое дерево графа содержит все вершины графа, то оно называется покрывающим деревом или остовом графа.
Алгоритм построения экстремального дерева предполагает соединение всех вершин графа с помощью путей наименьшей (наибольшей) длины. Типичной задачей, для решения которой необходим такой алгоритм, является проектирование дорог с твердым покрытием, соединяющих населенные пункты в сельской местности, проведение линии связи, водо- или газопровода с наименьшей суммарной длиной.
1) Составить план n вершин дерева.
2) Составить таблицу весов всех возможных связей между вершинами.
3) Выбрать ребро с наименьшим (наибольшим) весом и включить в дерево.
4) На следующем шаге рассмотреть минимальное по весу ребро из оставшихся и, если оно не образует цикл с ранее включенными ребрами, то добавить к дереву. Если имеется несколько таких ребер, то выбирается любое, при этом задача имеет альтернативное решение.
5) Построение заканчивается после разбора n–1 ребра.
Задача. Телевизионная компания планирует подключение к своей кабельной сети пяти новых районов. На рисунке 12.8 показана структура планируемой сети и расстояния (в км) между районами и телецентром. Необходимо спланировать наиболее экономичную кабельную сеть.
Решение задачи сводится к построению экстремального дерева графа.
Занесем данные задачи в следующую таблицу:
Источник
Деревья покрытия. Остовы
- Пусть
– связный граф. Деревом покрытия графа
называется подграф, который является деревом, и множество вершин которого совпадает с множеством вершин графа
.
Заметим, что связный граф может иметь много различных деревьев покрытия. (Пример)
- Каждый связный граф содержит в себе дерево покрытия.
- Пусть
– связный граф. Если
не содержит циклов, то доказывать ничего не надо, ибо
– сам по себе – дерево покрытия.
Предположим, что 




- Пусть
– несвязный граф. Остовом (или каркасом) графа
называется объединение деревьев покрытия всех его компонент связности.
Очевидно, что в каждом графе существует остов: разрушая в каждой компоненте связности циклы, т.е. удаляя лишние ребра, придем к остову.
- Число ребер произвольного графа
, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно
.
- Если
– граф
является одной из компонент связности графа
, то для превращения его в остовное дерево нужно удалить
подходящих ребер, т.к. в дереве число ребер
. Суммируя по всем
компонентам, получим требуемое.
- Число
называется цикломатическим числом графа
.
-
Раскраска графов
- Пусть
— некоторый граф,
натуральное число. Произвольная функция вида
называется
раскраской графа
.
- Раскраска называется правильной, если
любых смежных вершин
и
- Граф, для которого
правильная
раскраска, называется
раскрашиваемым (или просто раскрашиваемым
цветами).
Правильную 

- Минимальное число
, при котором граф
является
раскрашиваемым, называется хроматическим числом этого графа и обозначается
. Если
, то граф
называется
хроматическим. Правильная
раскраска
при
называется минимальной раскраской.
- Одна из правильных 4-раскрасок.



Алгоритм правильной раскраски
- произвольной вершины
графа
применим цвет 1.
- Если вершины
раскрашены
цветами
,
, то новой произвольно взятой вершине
припишем цвет, не использованный при раскраске вершин из её окружения (т.е. инцидентных ей вершин).
Раскраска, к которой приводит данный алгоритм, называется последовательной. Для некоторых графов (напр., для полных двудольных) последовательная раскраска является минимальной. В общем случае это не так.
Источник
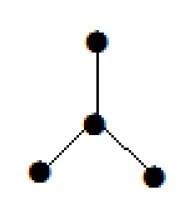
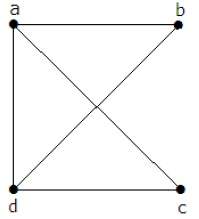

 – связный граф. Деревом покрытия графа
– связный граф. Деревом покрытия графа  называется подграф, который является деревом, и множество вершин которого совпадает с множеством вершин графа
называется подграф, который является деревом, и множество вершин которого совпадает с множеством вершин графа  .
. – связный граф. Если
– связный граф. Если  не содержит циклов, то доказывать ничего не надо, ибо
не содержит циклов, то доказывать ничего не надо, ибо  – сам по себе – дерево покрытия.
– сам по себе – дерево покрытия. – несвязный граф. Остовом (или каркасом) графа
– несвязный граф. Остовом (или каркасом) графа  называется объединение деревьев покрытия всех его компонент связности.
называется объединение деревьев покрытия всех его компонент связности. , которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно
, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно  .
. – граф
– граф  является одной из компонент связности графа
является одной из компонент связности графа  , то для превращения его в остовное дерево нужно удалить
, то для превращения его в остовное дерево нужно удалить 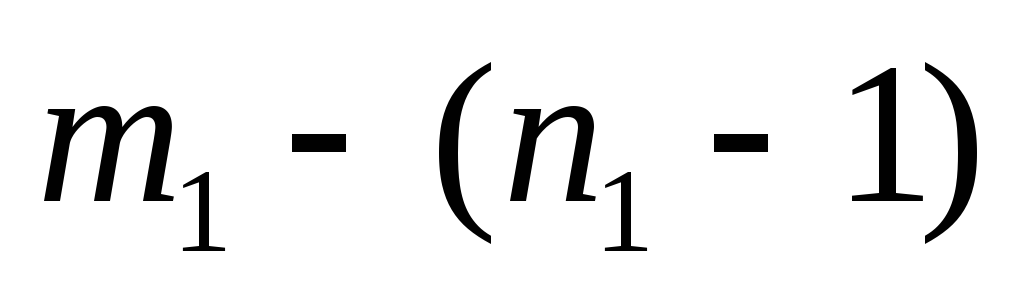 подходящих ребер, т.к. в дереве число ребер
подходящих ребер, т.к. в дереве число ребер  . Суммируя по всем
. Суммируя по всем  компонентам, получим требуемое.
компонентам, получим требуемое. называется цикломатическим числом графа
называется цикломатическим числом графа  .
. — некоторый граф,
— некоторый граф,  натуральное число. Произвольная функция вида
натуральное число. Произвольная функция вида  называется
называется  раскраской графа
раскраской графа  .
. любых смежных вершин
любых смежных вершин  и
и 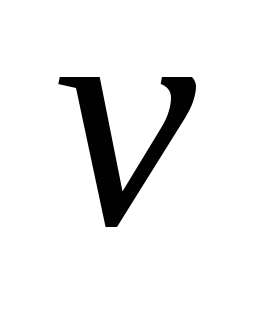
 правильная
правильная  раскраска, называется
раскраска, называется 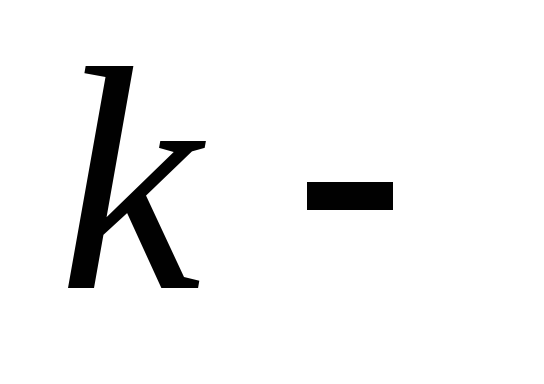 раскрашиваемым (или просто раскрашиваемым
раскрашиваемым (или просто раскрашиваемым  цветами).
цветами). , при котором граф
, при котором граф  является
является  раскрашиваемым, называется хроматическим числом этого графа и обозначается
раскрашиваемым, называется хроматическим числом этого графа и обозначается  . Если
. Если  , то граф
, то граф  называется
называется  хроматическим. Правильная
хроматическим. Правильная  раскраска
раскраска  при
при  называется минимальной раскраской.
называется минимальной раскраской. графа
графа  применим цвет 1.
применим цвет 1. раскрашены
раскрашены  цветами
цветами  ,
,  , то новой произвольно взятой вершине
, то новой произвольно взятой вершине  припишем цвет, не использованный при раскраске вершин из её окружения (т.е. инцидентных ей вершин).
припишем цвет, не использованный при раскраске вершин из её окружения (т.е. инцидентных ей вершин).