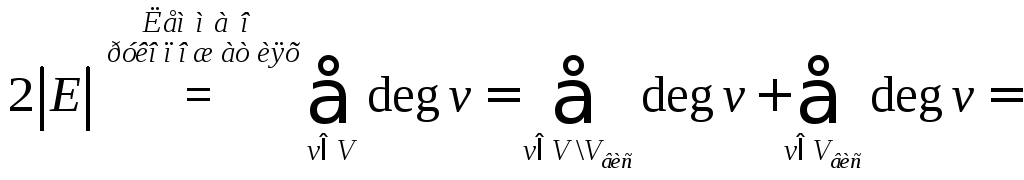Деревья
Существует один простой и важный тип графов, которому разные авторы дали одинаковое название, это- деревья. Деревья важны не только потому, что они находят приложения в различных областях знания, но и в силу особого положения их в самой теории графов. Последнее вызвано предельной простотой строения деревьев. Часто при решении какой-либо задачи о графах ее сначала исследуют на деревьях. Примером служит гипотеза Улама, приведенная в гл. 2.
Ниже дано несколько определений дерева. Сначала в геометрических терминах изучается понятие центральности дерева. Затем рассматриваются деревья, естественным образом связанные с произвольным связным графом, именно деревья блоков и точек сочленения. Наконец, будет показано, как каждый остов графа G приводит к набору его независимых циклов, и обратно, для каждого ко-остова можно построить набор независимых коциклов.
Описание деревьев
Граф называется ациклическим, если в нем нет циклов.Дерево— это связный ациклический граф. Каждый граф, не содержащий циклов, называетсялесом. Таким образом, компонентами леса являются деревья. Существуют 23 различных дерева с восемью вершинами. Известны и другие определения дерева. В теореме 4.1 отражены некоторые из них.
Теорема.Для графа G следующие утверждения эквивалентны:
(2) любые две вершины в G соединены единственной простой цепью;
(3) G — связный граф и p=q+1;
(4) G — ациклический граф и p=q+1;
(5) G — ациклический граф, и если любую пару несмежных вершин
соединить ребром х, то в графе G + x будет точно один простой цикл;
(6) G — связный граф, отличный от Кр для р>=З, и если любую пару несмежных вершин соединить ребром х, то в графе G + x будет точно один простой цикл;
(7) G — граф, отличный от КзUК1 и КзUК2, p=q+1, и если любую пару несмежных вершин соединить ребром х, то в графе G + x будетточно один простой цикл.
Доказательство.(1) влечет (2). Поскольку G — связный граф, то любые две его вершины соединены простой цепью. Пусть Р1 и P2— две различные простые цепи, соединяющие вершины и и v, и пусть w — первая вершина, принадлежащая Р2 (при переходе по P1 из и в v), такая, что w принадлежит и P1 и Р2, но вершина, предшествующая ей в P1, не принадлежит Р2. Если w’ — следующая за w вершина в Р1 принадлежащая также Р2, то сегменты (части) цепей P1 и Р2, находящиеся между вершинами w и w’, образуют простой цикл в графе G. Поэтому, если G — ациклический граф, то между любыми двумя его вершинами существует самое большее одна простая цепь.
(2) влечет (3). Ясно, что граф G — связный. Соотношение р =q+1 докажем по индукции. Утверждение очевидно для связных графов с одной и двумя вершинами. Предположим, что оно верно для графов, имеющих меньше р вершин. Если же граф G имеет р вершин, то удаление из него любого ребра делает граф G несвязным в силу единственности простых цепей; более того, получаемый граф будет иметь в точности две компоненты. По предположению индукции в каждой компоненте число вершин на единицу больше числа ребер. Таким образом, общее число ребер в графе G должно равняться р — 1.
(3) влечет (4). Предположим, что в графе G есть простой цикл длины п. Этот цикл содержит nвершин иnребер, а для любой из р —nвершин, не принадлежащих циклу, существует инцидентное ей ребро, которое лежит на геодезической, идущей от некоторой вершины цикла. Все такие ребра попарно различны; отсюда q>p, т. е. пришли к противоречию.
(4) влечет (5). Так как G — ациклический граф, то каждая его компонента является деревом. Если всего k компонент, то, поскольку в каждой из них число вершин на единицу больше числа ребер, имеем p = q + k. В нашем случае должно быть k=1, так что G — связный граф. Таким образом, G — дерево и любые две его вершины соединяет простая единственная цепь. Если к дереву G добавить ребро uv, то ребро вместе с единственной простой цепью, соединяющей вершины uи v, образует простой цикл, который также единствен в силу единственности простой цепи.
(5) влечет (6). Поскольку каждый полный граф КР для р>3 содержит простой цикл, граф G не может быть одним из этих графов. Граф G должен быть связным, так как в ином случае можно было бы добавить ребро х, соединяющее две вершины из разных компонент графа G, и граф G + x был бы ациклическим.
(6) влечет (7). Докажем, что любые две вершины графа G соединены единственной простой цепью, а тогда, поскольку (2) влечет (3), получим p=q+1. Ясно, что в графе G любые две вершины соединены простой цепью. Если какая-то пара вершин графа G соединена двумя простыми цепями, то из доказательства того, что (1) влечет (2), следует наличие у графа G простого цикла Z. В Z не может быть более трех вершин, так как иначе, соединив ребром х две несмежные вершины в Z, получим граф G + x, имеющий более одного простого цикла (если же в Z нет несмежных вершин, то в графе G более одного цикла). Таким образом, цикл Z есть К.3, и он должен быть собственным подграфом графа G, поскольку по предположению G не является полным графом КР с р>3. Так как G — связный граф, то можно предположить, что в G есть другая вершина, смежная с некоторой вершиной подграфа К3. Тогда ясно, что если к графу G добавлять ребро, то его можно добавить так, чтобы в графе G + x образовались, по крайней мере два простых цикла. Если больше нельзя добавить новых ребер, не нарушая для графа G второго условия из (6), то G есть КР с р>3 вопреки предположению.
(7) влечет (1). Если граф G имеет простой цикл, то этот цикл должен быть треугольником, являющимся компонентой графа G, что было показано в предыдущем абзаце. В этой компоненте соответственно три вершины и три ребра. Все остальные компоненты графа G должны быть деревьями, но для того, чтобы выполнялось соотношение p = q + l, должно быть не более одной компоненты, отличной от указанного треугольника. Если это дерево содержит простую цепь длины 2, то к графу G можно так добавить ребро х, чтобы образовать в графе G + x два простых цикла. Следовательно, этим деревом может быть или К1 или K2. Значит, граф G — или Кз U K1или К3U К2, а эти графы мы исключили из рассмотрения. Таким образом, G- ациклический граф. Но если G — ациклический граф и p=q+1, то G связен, поскольку (4) влечет (5), а (5) влечет (6). Итак,
G -дерево, и теорема доказана.
Так как для нетривиального дерева di = 2q=2(p— 1), то в дереве должно быть, по крайней мере, две вершины со степенями, меньшими 2.
Следствие.В любом нетривиальном дереве имеется, по крайней мере, две висячие вершины.
Этот результат также следует из теоремы.
Источник
3.9. Деревья и леса
Каждая компонента связности леса – дерево, следовательно, для 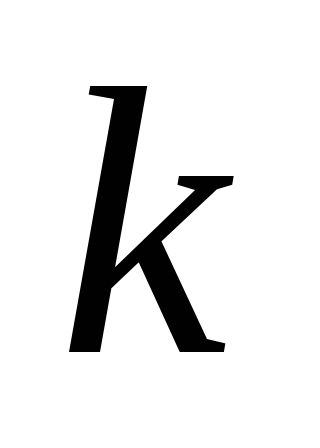

П


Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях). Для графа следующие утверждения равносильны:
- Граф
— дерево.
ациклический и
.
связный и
.
связный и каждое его ребро является мостом.
- Любые две вершины графа
можно соединить, притом единственной, простой цепью.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Доказательство.Доказательство проведем по следующей схеме:


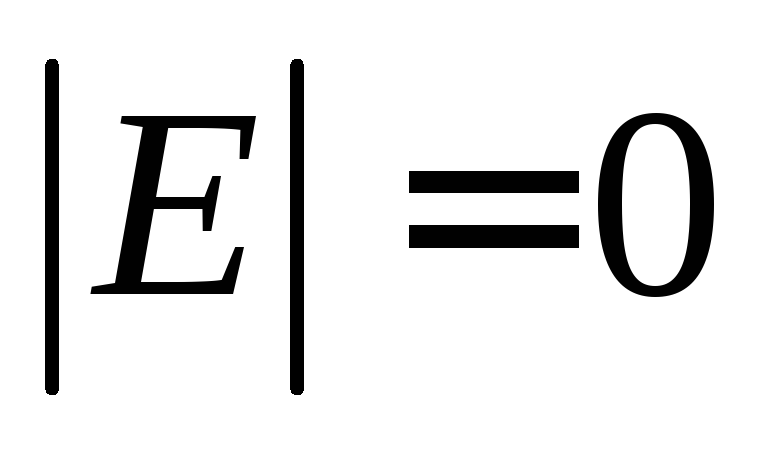
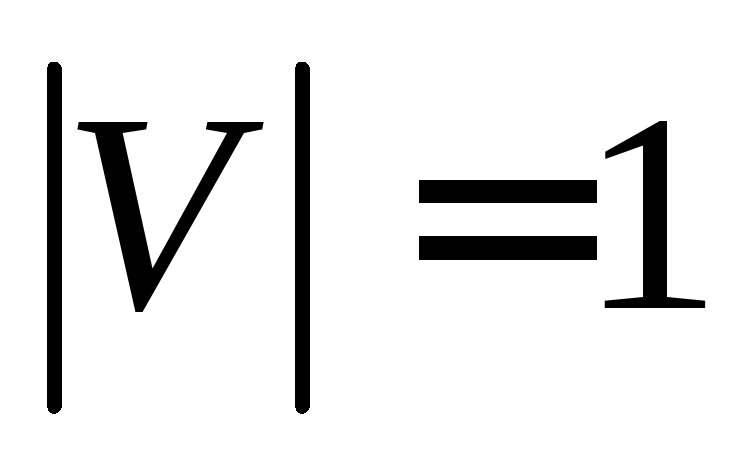
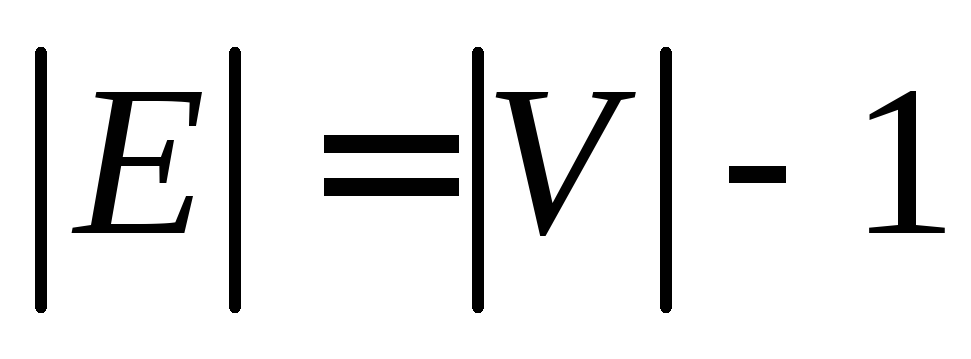




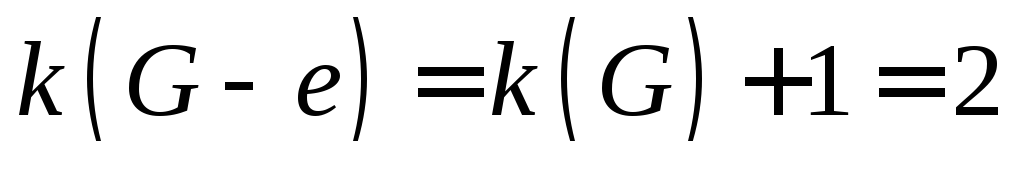
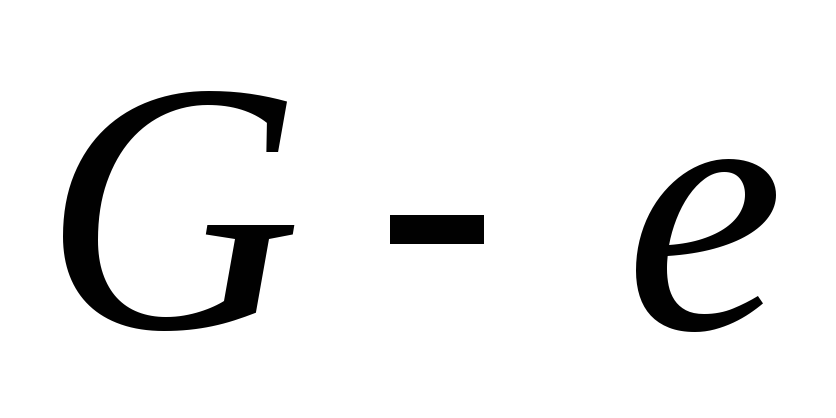
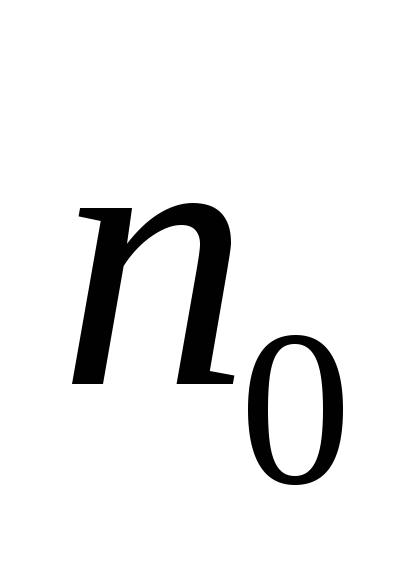
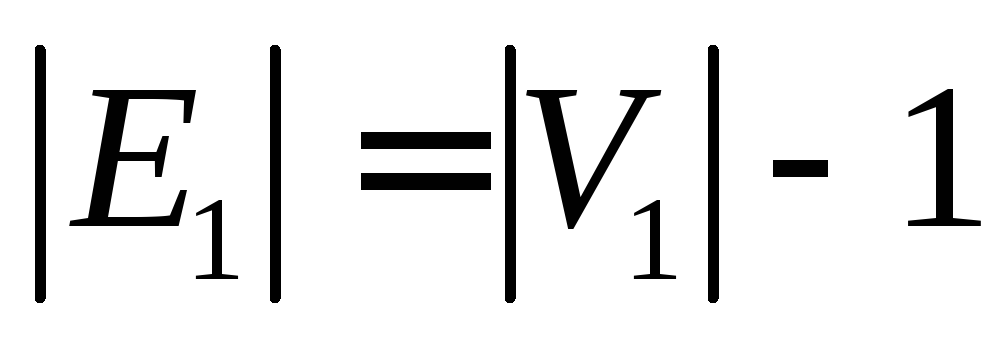
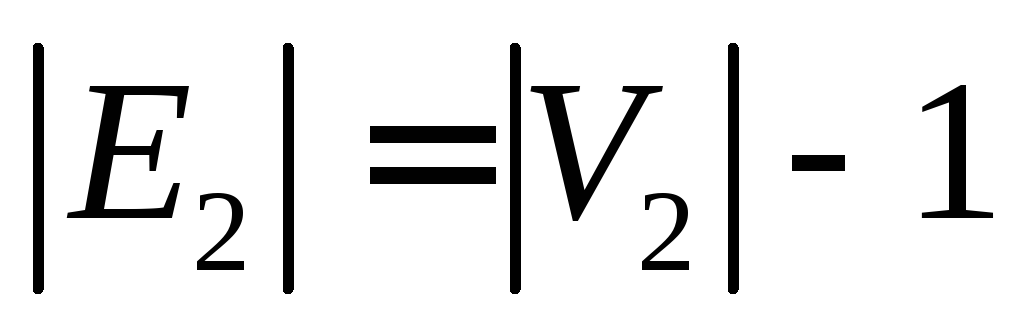



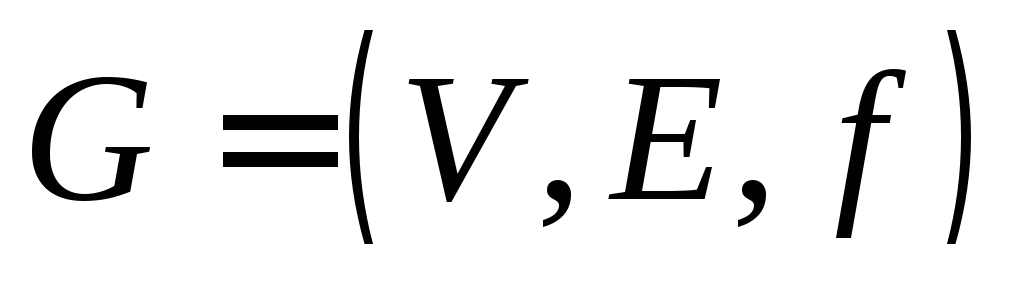
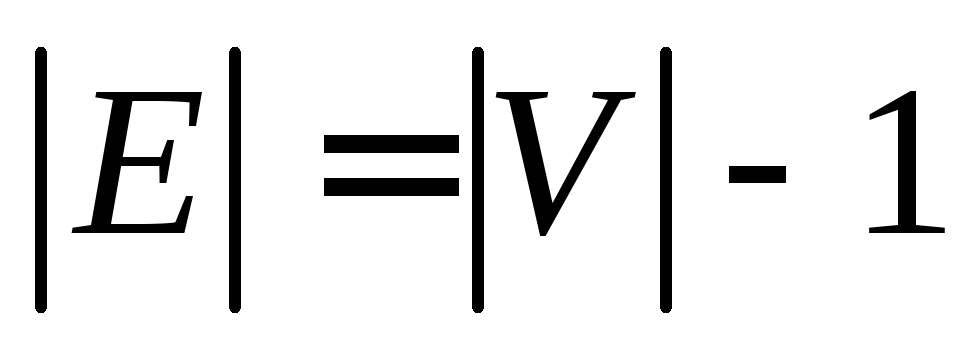












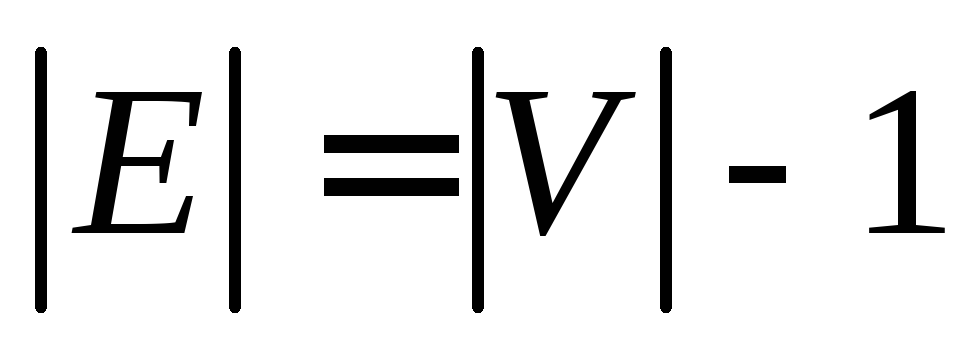



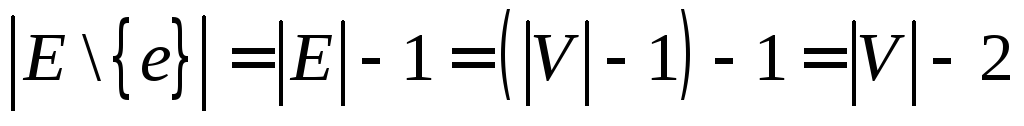
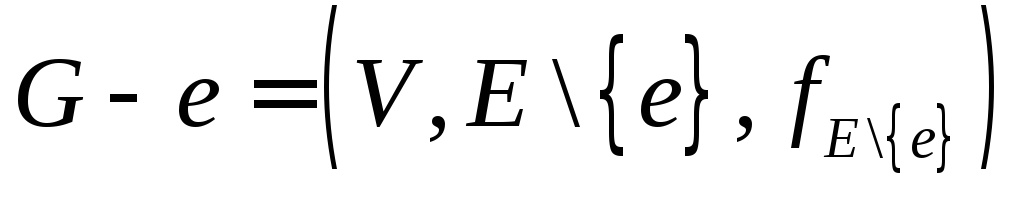











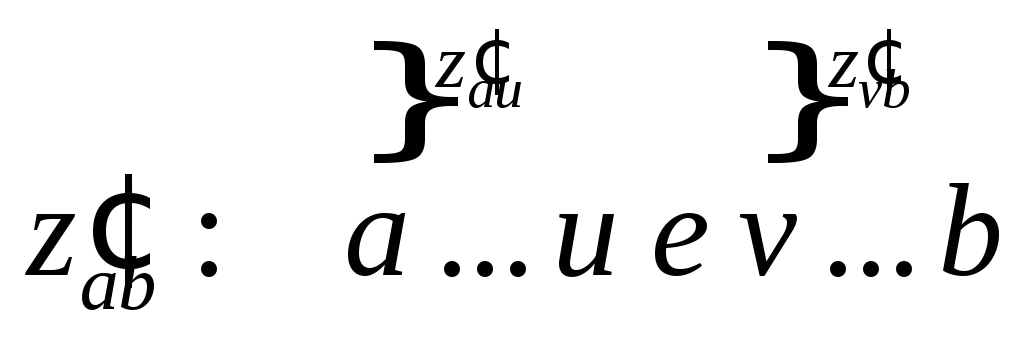





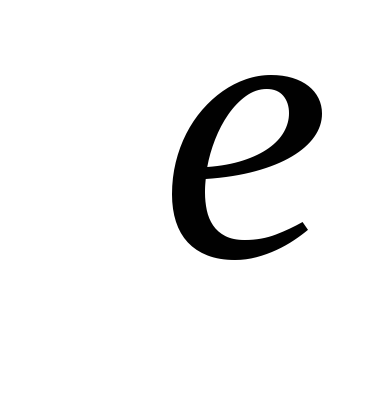






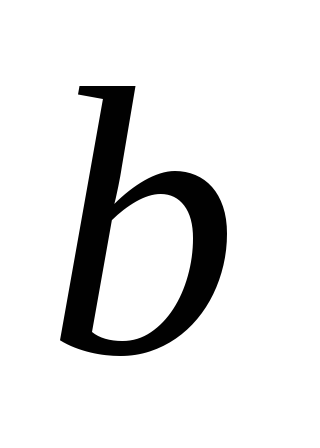







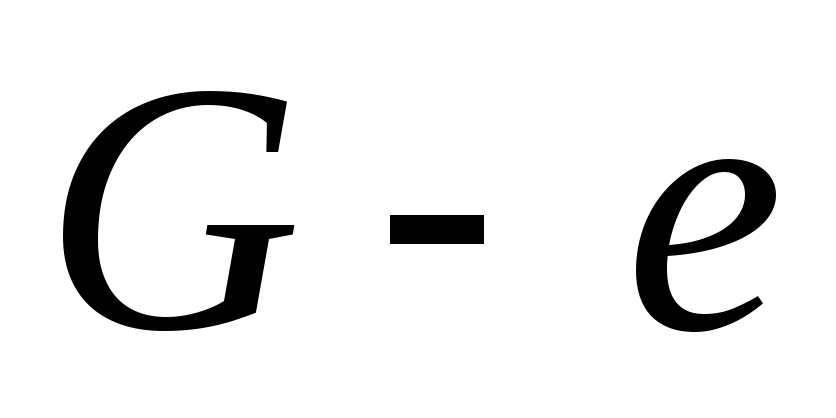









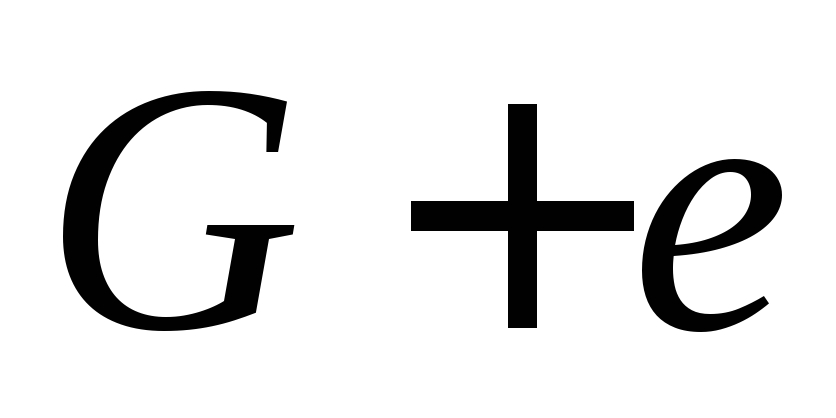

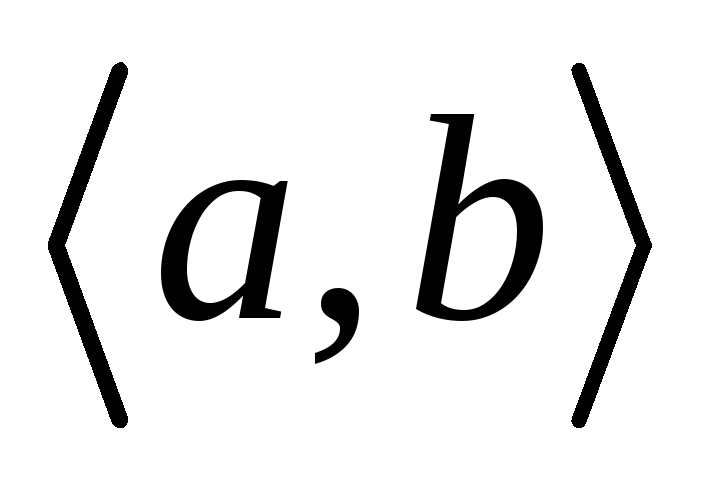

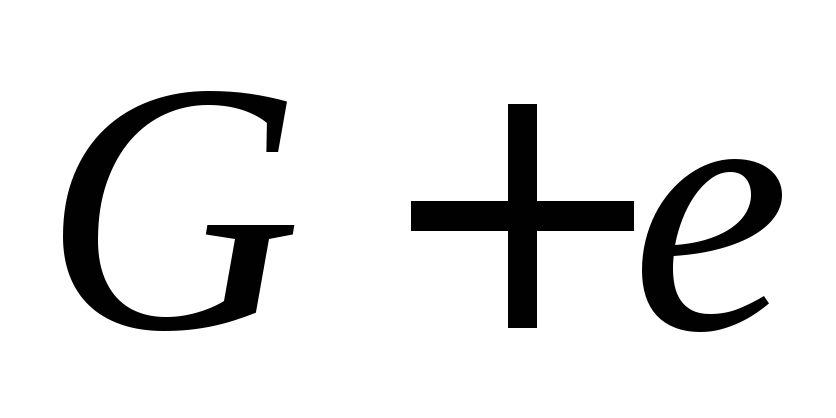

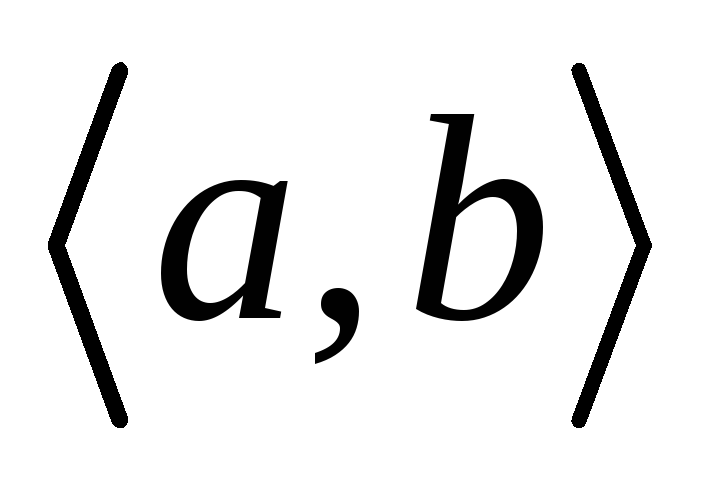







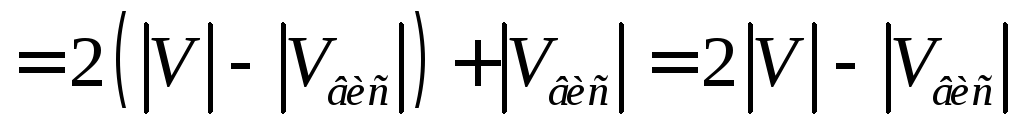




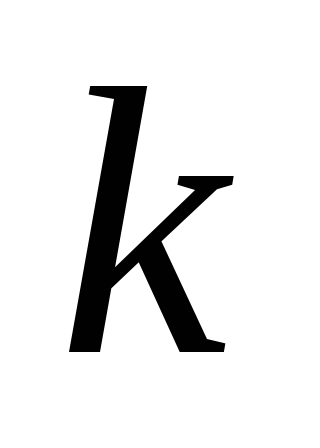

Источник

 — дерево.
— дерево. ациклический и
ациклический и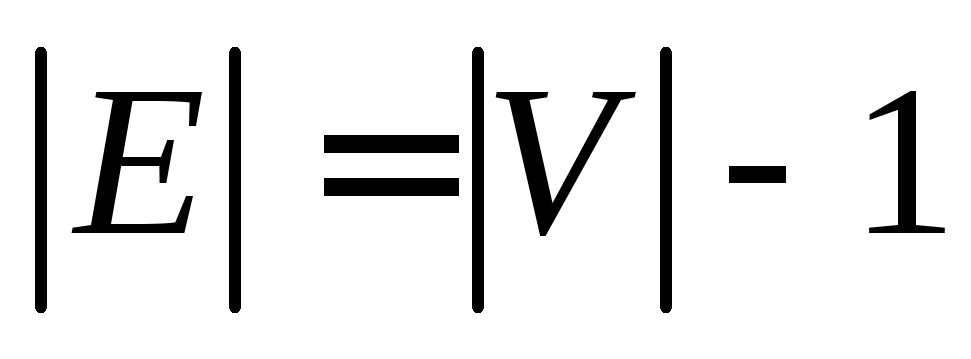 .
. связный и
связный и .
. связный и каждое его ребро является мостом.
связный и каждое его ребро является мостом. можно соединить, притом единственной, простой цепью.
можно соединить, притом единственной, простой цепью. ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.