Деревья графы построение граф

3 Покрывающие деревья (остовы)

Цикломатическим числом неориентированного графа G называется величина γ(G) = т — п + k, где т — число ребер, п — число вершин, k — число связных компонент. Для дерева и леса γ (G) = 0, для других графов γ (G) > 0.

Остовом, или покрывающим деревом, связного графа G=(V, E) называется часть G, которая содержит все его вершины и является деревом. Хордой остова графа G называется ребро G, не принадлежащее остову.

Очевидно, что любой связный граф имеет хотя бы один остов, а любой несвязный граф остова не имеет.

В последующем алгоритме части исходного графа G, которые возникают в процессе построения покрывающего дерева, будем называть букетами.

Алгоритм построения покрывающего дерева для произвольного невзвешенного графа g

1. Выбрать любое ребро G, не являющееся петлей. Пометить его меткой α и объявить букетом это ребро вместе с его концевыми вершинами.

2. Выбрать любое непомеченное ребро G, не являющееся петлей:

а) если один из концов выбранного ребра принадлежит построенному ранее букету В, а другой конец свободен (не принадлежит ни одному букету), пометить выбранное ребро меткой α, включить его вместе со свободным концом в букет В и перейти к шагу 3;

б) если оба конца выбранного ребра свободны, поме­тить его меткой а, объявить это ребро вместе с его конце­выми вершинами новым букетом и перейти к шагу 3;

в) если концы выбранного ребра принадлежат разным построенным ранее букетам В и С, пометить выбранное ребро меткой α, включить его и букет С в букет В и перейти к шагу 3;

г) если оба конца выбранного ребра принадлежат одному букету, пометить его меткой β и перейти к шагу 3;

д) если непомеченных ребер нет, закончить алгоритм.

3. Если все вершины графа G вошли в один букет, закончить алгоритм. Если нет, перейти к шагу 2.

Алгоритм выделения минимального остовного дерева в неориентированном взвешенном графе g

1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему двумя вершинами оно образует подграф G₂ графа G. Положим i:=2.
2. Если i=n(G), то задача решена и G_i – искомое минимальное остовное дерево графа G. Иначе переходим к шагу 3).
3. Строим граф G_i+1. Для этого добавим к графу G_i новое ребро минимальной длины из оставшихся, которое инцидентно какой-либо вершине графа G_i и одновременно вершине, не содержащейся в G_i. Вместе с этим ребром включаем в G_i+1 и эту инцидентную ему вершину. Присваиваем i:=i+1 и переходим к шагу 2.

Лекция 12 Двудольные и планарные графы

1 Двудольные графы

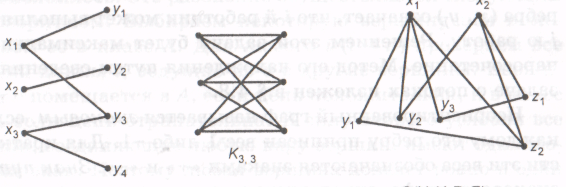
Двудольным графом G=(X, Y, Е) называется неориентированный граф, вершины которого можно разбить на два класса X и Y так, что концы каждого ребра принадлежат разным классам. Двудольный граф называется полным, если каждая вершина одной доли соединена с каждой вершиной другой доли, полный двудольный граф принято обозначать символом 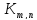гдет = |Х|, n = . Введенные понятия допускают естественное обобще-ие. Неориентированный граф называется k-дольным, если его вершины можно разбить на k классов так, что концы каждого ребра принадлежат разным классам. Полный k-дольный граф — это k-дольный граф, в котором каждая вершина одной доли соединена с каждой вершиной всех остальных долей. Пример. На рисунке 24 представлены двудольный граф G=(X, Y, Е), полный двудольный граф К_3,3 и трехдольный граф G=(X, Y, Z, Е), где X = 1 x₂>, Y = 1 y₂, y₃>, Z = 1 z₂>. G=(X, Y, Е) G=(X, Y, Z, Е) Рисунок 24 – Двудольные графы Теорема. Граф является двудольным, если и только если длины всех его простых циклов четны. Паросочетанием в неориентированном графе называется множество попарно несмежных ребер. Задача о максимальном паросочетании заключается в нахождении паросочетания максимальной мощности. Для двудольного графа одной из наиболее известных интерпретаций задачи о максимальном паросочетании является задача о назначениях, которая заключается в следующем. Имеется т работников и п работ. Каждый работник способен выполнять несколько работ; каждую работу могут выполнять несколько работников. Требуется определить назначения по принципу «один работник — одна работа» так, чтобы загрузить максимальное число работников. Условия этой задачи представляются в виде двудольного графа, в котором вершины класса X соответствуют работникам, вершины класса Y- работам, а наличие ребра (x_i, y_j) означает, что i-й работник может выполнять j-ю работу. Решением этой задачи будет максимальное паросочетание, которое находится путем сведения к задаче о потоках.

Источник

3.5. Дерево. Остов

т. е. число ребер в дереве на единицу меньше числа вершин.

Ниже на рис. 3.7 приведены примеры деревьев.

Пример 3.7

Остов — это подграф (частичный граф), который может быть построен из графа удалением некоторых ребер и который является деревом.

В общем случае для графа можно построить несколько остовов. Для приведенного ниже графа построен один из возможных вариантов остова.

Для несвязного графа рассматриваются отдельные его компоненты. Остов такого графа — совокупность его компонент.

3.5.1. Алгоритм построения произвольного остова. Рассмотрим словесное описание алгоритма:

1. Для каждой компоненты i графа выполняем пункты 2 и 3.

2. Строим частичный подграф, содержащий все n_i вершин i-й компоненты и не содержащий ребер (0- граф).

3. Если в текущий частичный граф включены уже n_i-1 ребер, то остов для компоненты i построен, иначе выбираем очередное ребро компоненты и пытаемся его включить в текущий граф.

Если в текущем графе это не приводит к образованию цикла, то включаем ребро, иначе — не включаем. Ребро считаем рассмотренным. Выполняем п. 3.

Так как цикл не образовался, то все рёбра с номерами 1, 2, 3, 4 включены в остов. Проверяем по (3.3): m=4, n=5 и 4=5-1.

3.5.2. Алгоритм построения минимального остова. Для взвешенного графа остов с наименьшей суммой весов для вошедших в него рёбер называется минимальным (кратчайшее связное дерево).

Если в сформулированном ранее алгоритме построения обычного остова рассматривать рёбра в порядке возрастания их весов, то будет построен минимальный остов.

3.5.3. Алгоритм построения системы независимых циклов графа

1. Строится произвольный остов графа. В исходном графе отмечаются рёбра, не включенные в остов.

2. Выбирается очередное отмеченное ребро и строится цикл, содержащий это ребро и рёбра остова. Рассмотренное ребро отмечается и, если есть ещё не отмеченные рёбра, то выполняется пункт 2, иначе — пункт 3.

3. По формуле Эйлера (3.2) производится проверка числа построенных циклов.

Пример 3.12

Рис 3.12

1)(X2,X4)(X4,X5)(X5,X1)(X1,X3);

2)(X3,X5)(X5,X1)(X1,X2)(X2,X3);

3)(X3,X4)(X4,X5)(X5,X1)(X1,X2)(X2,X3).

3.6. Алгоритм кратчайшей раскраски графа

Раскраска представляет собой маркирование вершин графа таким образом, чтобы у смежных вершин маркеры не совпадали. Вместо красок используются числа 0, 1, 2… Условие оптимальности раскрашивания — использование минимального числа красок . Это число называется хроматическим числом графа.

Граф, который можно представить на плоскости без пересечения его рёбер, называется плоским.

Теорема. Для плоских графов   4.

Отметим, что проблема раскраски — алгоритмически неразрешима.

Пример 3.13. Рассмотрим граф G (рис. 3.13). Убедившись в том, что он – плоский (ребро (x₁, x₅) может быть проведено вне контура (x₁, x₂, x₃, x₅)), произведём его раскраску. Имеем: =3 (краски  0, 1, 2).

В общем случае строим таблицу для определения максимальных внутренне-устойчивых подмножеств множества вершин графа, т. е. множеств несмежных вершин графа. Строки таблицы – внутренне-устoйчивые множества. Столбцы этой таблицы — номера вершин графа, а последний столбец — имя очередного максимального внутренне-устойчивого подмножества.

Несмежные вершины отмечены в таблице единицами. Далее решается задача построения одного кратчайшего покрытия (методом минимального столбца — максимальной строки). Вершины, принадлежащие каждому подмножеству, вошедшему в найденное кратчайшее покрытие, окрашивается одной краской. Если некоторая вершина принадлежит нескольким вошедшим в покрытие подмножествам, то она в одном остаётся, из остальных исключается. Для нашего примера получим три подмножества: Y₁,Y₂,Y₃, определяющие три краски 0, 1, 2 соответственно.

как показано на рис. 3.13, если x₁ покрасить краской 0, то все смежные с ней вершины x₂, x₃, x₄, x₅ нельзя покрасить 0. Вершины x₂, x₄ — смежные, для них необходимы две разные краски (1 и 2); аналогично  для x₃, x₄. Однако вершины x₂, x₃ — не смежные, и их можно покрасить одной краской.

Таким образом, изображенная на рис. 3.13 раскраска — минимальна.

Источник

Лекция 11

Дерево. Лес (ациклический граф). Остовный подграф. Остов. Взвешенный граф. Минимальный остов. Кодирование деревьев.

Базовые понятия и утверждения

1. Определение и основные свойства деревьев.

Определение. Граф называется деревом, если он связный и в нем нет циклов.

Одноэлементный граф, т.е. граф, имеющий одну вершину и не имеющий ребер, также считается деревом.

Граф называется лесом (или ациклическим графом), если в нем нет циклов. Очевидно, что каждая компонента связности леса — дерево.

Пример 1. Граф (рис. 3.19) не является ни деревом, ни лесом. Граф (рис. 3.20) — дерево. Граф (рис. 3.21) — лес, состоящий из четырех деревьев.

Пример 2. Представьте диаграммами все (с точностью до изоморфизма) деревья с пятью вершинами.

◄ Имеется три различных (с точностью изоморфизма) дерева с пятью вершинами (рис. 3.22 — 3.24). ►

Деревья обладают рядом характеристических свойств, по наличию или отсутствию каждого их которых в рассматриваемом графе можно определить, является граф деревом или нет. Перечислим эти свойства:

1) граф — дерево в том и только в том случае, когда в нем нет циклов и ;

2) граф — дерево в том и только в том случае, когда он связный и ;

3) граф — дерево в том и только в том случае, когда он связный, и каждое его ребро является мостом;

4) граф — дерево в том и только в том случае, когда любые две вершины графа можно соединить простой цепью, притом единственной;

5) граф — дерево в том и только в том случае, когда в нем нет циклов и добавление к нему нового ребра приводит к образованию единственного простого цикла.

Также приведем одно из характеристических свойств леса: граф , имеющий компонент связности, является лесом в том и только в том случае, когда .

2. Остовы графа. Подграф графа называется остовным подграфом, если множество его вершин совпадает с множеством вершин графа .

Остовом обыкновенного графа называется его остовный подграф, являющийся деревом.

Пусть — связный граф. Если содержит хотя бы один цикл, то удалив из графа некоторое ребро этого цикла, мы уменьшим число циклов графа по крайней мере на единицу, сохранив при этом его связность. Ясно, что, последовательно разрушая циклы данного графа, можно прийти к остову графа. Поскольку дерево с вершинами имеет ровно ребро, то для получения остова нужно удалить из графа ребро, т.е. число ребер, равное цикломатическому числу связного графа .

Пусть теперь — произвольный граф с компонентами связности. Из каждой компоненты связности этого графа удалим ребро так, чтобы получился остов этой компоненты. В результате получим некоторый остовный подграф графа . Подсчитаем общее число ребер, которое нам пришлось для этого удалить. Сложив равенства , , получим:

.

Таким образом, чтобы получить остовный подграф, нужно, последовательно разрушая циклы графа, удалить из него число ребер, равное его цикломатическому числу.

Пример 3. Построим остов графа , диаграмма которого изображена на рис. 3.25. Удалим из графа ребро ; получим граф (рис. 3.26). Из графа удалим ребро ; получим граф (рис. 3.27). Из графа удалим ребро ; получим граф (рис. 3.28), который является одним из остовов графа .

Источник