Деревья графы висячие вершины

Содержание

Art of Math
Лекция № 14. Деревья
Важнейшие классы графов

Art of Math

Начнем с определений.
Определение 10. Дерево — связный граф, в котором нет циклов.
Определение 11. Висячая вершина — это вершина, локальная степень которой равна 1.

В доказательстве теоремы Кэли нам поможет небольшая лемма.

Лемма (Теорема 5). В любом дереве найдутся по-крайней мере две висячие вершины.

Доказательство. Выберем произвольную вершину дерева. Если ее степень 1, лемма доказана, иначе будем идти из нее по дереву, отмечая при обходе пройденные вершины, постоянно направляясь только в неотмеченные вершины. Понятно, что этот процесс кончится, тогда мы окажемся в вершине, из которой можно попасть либо только в помеченные вершины, либо совсем никуда. Если мы можем попасть в помеченные вершины, значит в графе есть цикл, что невозможно, значит степень вершины, в которой мы оказались равна 1. То есть, одну висячую вершину мы получили. Теперь снова сделаем все вершины непомеченными и повторим процесс для полученной нами висячей вершины, получив вторую висячую вершину. Лемма доказана.

Теорема 6 (Кэли). Число различных деревьев, которые можно построить на множестве V из N вершин, равно N^(N-2).

Доказательство.
Пронумеруем вершины от 1 до N. Рассмотрим произвольное дерево T такое, что множество его вершин совпадает с V. Выберем в нем висячую вершину с наименьшим номером, которая соединена с вершиной b1, удалим ее вместе с ребром из T, получив дерево T1. Будем вновь проделывать такие же операции с получающимися деревьями, пока оставшийся граф не будет представлять из себя две вершины при ребре. Таким образом, мы получим последовательность bi=.
Докажем теперь, что каждая такая последовательность однозначно задает дерево. Просто приведем алгоритм, который однозначно восстанавливает дерево. Алгоритм рекуррентный, докажем его по индукции.
Для N=3, восстановление очевидно.
Скажем сперва, что достаточно очевидно, что те числа от 1 до N, которых нет в bi, являются висячими вершинами изначального дерева T. Тогда возьмем самое маленькое такое число А. Понятно, что в изначальном дереве Т оно соединено ребром с вершиной b1. Проведем такое ребро. Теперь рассмотрим весь наш граф без вершины А и ребра (A, b1). Далее по индукции. Заметим, что минимальную вершину следует выбирать из тех, которые подходят по описанному условию и еще не были выбраны.Таким образом, мы установили, что каждая такая последовательность однозначно задает дерево. Количество таких последовательностей равно N^(N-2), что очевидно.
Теорема доказана.

Источник

Лекция № 14. Деревья

Основные определения

Дерево – связный граф без циклов. Лес (или ациклический граф) – неограф без циклов. Компонентами леса являются деревья. Теорема 14.1.Для неографаGсnвершинами без петель следующие условия эквивалентны:

G– дерево;
G– связной граф, содержащийn– 1 ребро;
G– ациклический граф, содержащийn– 1 ребро;
Любые две несовпадающие вершины графаGсоединяет единственная цепь;
G– ациклический граф, такой, что если в него добавить одно ребро, то в нем появится ровно один цикл.

Теорема 14.2.НеографGявляется лесом тогда и только тогда, когда коранг графаv(G)=0. Висячая вершина в дереве – вершина степени 1. Висячие вершины называются листьями, все остальные – внутреннимивершинами. Если в дереве особо выделена одна вершина, называемая корнем, то такое дерево называется корневым, иначе – свободным. Корневое дерево можно считать орграфом с ориентацией дуг из корня или в корень. Очевидно, что для любой вершины корневого дерева, кроме корня, . Для корня, для листьев. Вершины дерева, удаленные на расстояние k (в числе дуг) от корня, образуют k-й ярус (уровень) дерева. Наибольшее значение k называется высотой дерева. Если из какой-либо вершины корневого дерева выходят дуги, то вершины на концах этих дуг называют сыновьями (в английской литературе – дочери (daughter)).

Центроид дерева

Ветвь к вершине v дерева – это максимальный подграф, содержащий v в качестве висячей вершины. Вес вершиныk – наибольший размер ее ветвей. Центроид (или центр масс) дерева C – множество вершин с наименьшим весом: C = v| c(v) = >. Вес любого листа дерева равен размеру дерева. Высота дерева с корнем, расположенным в центроиде, не больше наименьшего веса его вершин. Свободное дерево порядка n с двумя центроидами имеет четное количество вершин, а вес каждого центроида равен n/2. Теорема 14.3 (Жордана).Каждое дерево имеет центроид, состоящий из одной или двух смежных вершин.Пример 14.1. Найти наименьший вес вершин дерева, изображенного на рис. 14.1, и его центроид. Рис. 14.1 Решение. Очевидно, что вес каждой висячей вершины дерева порядка n равен n – 1. Висячие вершины не могут составить центроид дерева, поэтому исключим из рассмотрения вершины 1, 2, 4, 6, 12, 13 и 16. Для всех остальных вершин найдем их вес, вычисляя длину (размер) их ветвей. Число ветвей вершины равно ее степени. Вершины 3, 5 и 8 имеют по две ветви, размеры которых равны 1 и 14. К вершине 7 подходят четыре ветви размером 1, 2, 2 и 10. Таким образом, ее вес . Аналогично вычисляются веса других вершин:,,. Минимальный вес вершин равен 8, следовательно, центроид дерева образуют две вершины с таким весом: 11 и 15.

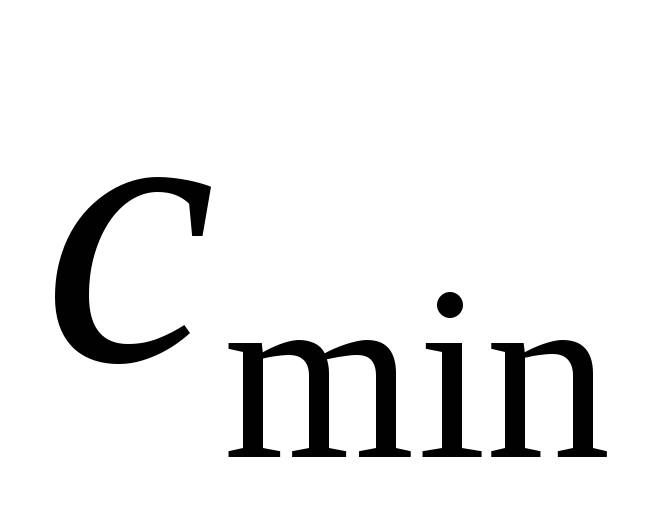
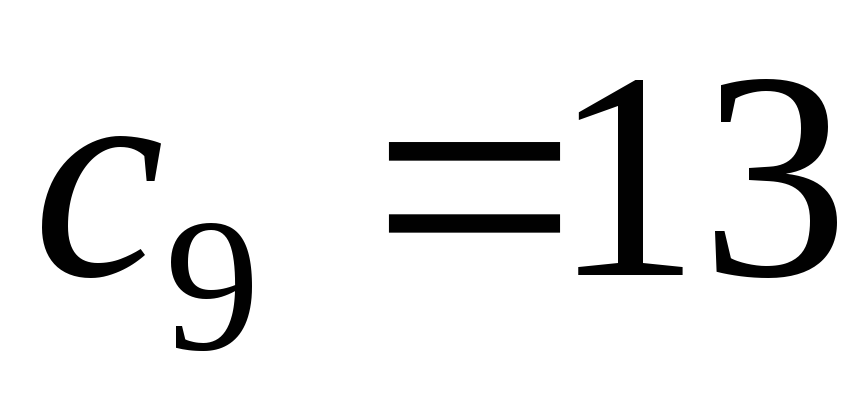
Десятичная кодировка

Деревья представляют собой важный вид графов. С помощью деревьев описываются базы данных, деревья моделируют алгоритмы и программы, их используют в электротехнике, химии. Одной из актуальных задач в эпоху компьютерных и телекоммуникационных сетей является задача сжатия информации. Сюда входит и кодировка деревьев. Компактная запись дерева, полностью описывающая его структуру, может существенно упростить как передачу информации о дереве, так и работу с ним. Существует множество способов кодировки деревьев. Рассмотрим одну из простейших кодировок помеченных деревьев с выделенным корнем – десятичную. Кодируя дерево, придерживаемся следующих правил.

Кодировка начинается с корня и заканчивается в корне.
Каждый шаг на одну дугу от корня кодируется единицей.
В узле выбираем направление на вершину с меньшим номером.
Достигнув листа, идем назад, кодируя каждый шаг нулем.
При движении назад в узле всегда выбираем направление на непройденную вершину с меньшим номером.

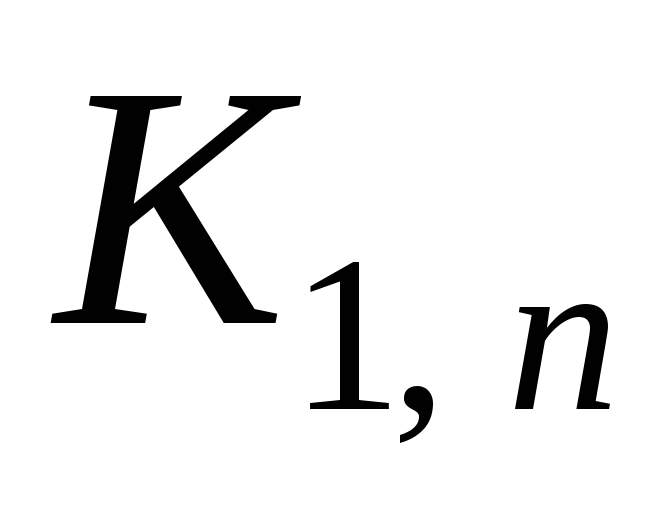
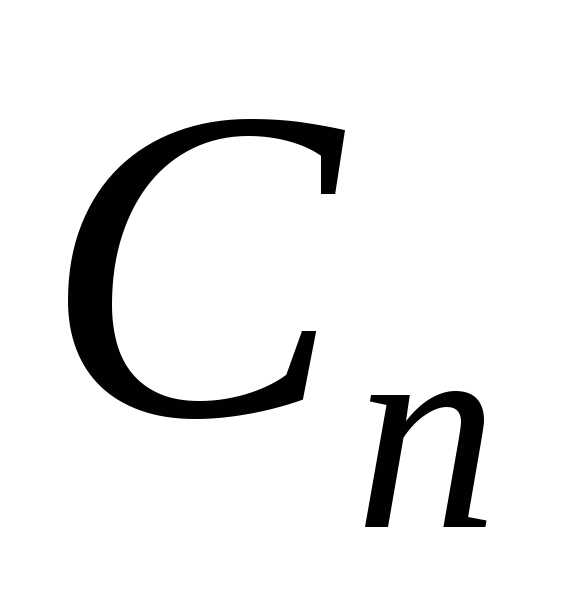
Кодировка в такой форме получается достаточно компактной, однако она не несет в себе информации о номерах вершин дерева. Существуют аналогичные кодировки, где вместо единиц в таком же порядке проставляются номера или названия вершин. Есть деревья, для которых несложно вывести формулу десятичной кодировки. Рассмотрим, например, графы-звезды , являющиеся полными двудольными графами, одна из долей которых состоит из одной вершины. Другое обозначение звезд –. На рис. 14.2 показаны звезды, а также приведены их двоичные и десятичные кодировки. Корень дерева располагается в центральной вершине звезды. Легко получить общую формулу: . (14.1) Рис. 14.2 Если корень поместить в любой из висячих вершин, то код такого дерева будет выражаться большим числом. Более того, существует зависимость. Аналогично рассматриваются и цепи (рис. 14.3). Цепи обозначаются как. Рис. 14.3 В звездах только два варианта расположения корня с различными десятичными кодировками. В цепи же число вариантов кодировок в зависимости от положения корня растет с увеличением n. Рассмотрим самый простой вариант, расположив корень в концевой вершине (листе). Для получим двоичную кодировку 10 и десятичную 2, для– 1100 и 12, для– 111000 и 56, для– 11110000 и 240. Общая формула для десятичной кодировки цепи с корнем в концевой вершине имеет вид . (14.2) Пример 14.2. Записать десятичный код дерева, изображенного на рис. 14.4, с корнем в вершине 3. Рис. 14.4 Решение. На основании правила кодировки, двигаясь по дереву, проставим в код единицы и нули. При движении из корня 3 к вершине 7 проходим четыре ребра. В код записываем четыре единицы: 1111. Возвращаясь от вершины 7 к вершине 2 (до ближайшей развилки), проходим три ребра. Записываем в код три нуля: 000. От вершины 2 к 5 и далее к 8 (меньший номер): 11; от 8 назад к 5 и от 5 к 9: 01; от 9 к корню 3: 000. И, наконец, от 3 к 6 и обратно: 10. В итоге, собирая все вместе, получим двоичный код дерева: 1 111 000 110 100 010. Разбивая число на тройки, переводим полученное двоичное представление в восьмеричное. Получаем . Затем переводим это число в десятичное:.

Для продолжения скачивания необходимо пройти капчу:

Источник

Важнейшие классы графов

Деревом называется связный граф , не имеющий циклов. В графе без циклов, таким образом, каждая компонента связности является деревом. Такой граф называют лесом .

P_<n data-lazy-src=

Из теоремы 2 «Маршруты, связность, расстояния» следует, что во всяком дереве, в котором не меньше двух вершин, имеется вершина степени 1. Такие вершины называют висячими вершинами , или листьями . В действительности легко доказать, что в каждом дереве не меньше двух листьев, а цепь »/> — пример дерева, в котором точно два листа.

В следующих двух теоремах устанавливаются некоторые свойства деревьев.

Теорема 1. Граф с ребрами является деревом тогда и только тогда, когда он удовлетворяет любым двум из следующих трех условий:

m=n-1

(1) связен;
(2) не имеет циклов;
(3) .

Первые два условия вместе составляют определение дерева. Покажем, что выполнение любых двух из условий (1)-(3) влечет за собой выполнение третьего.

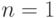(1) и (2) $\Rightarrow$ (3). Индукция по числу вершин. При n=1 утверждение очевидно. При $n\ge 2$ в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность, очевидно, сохранится. В этом новом дереве n-1 вершин и, по предположению индукции, n-2 ребра. Следовательно, в исходном дереве было n-1 ребро.

(2) и (3) $\Rightarrow$ (1). Пусть в графе, не имеющем циклов, n-1 ребро, а его компонентами связности являются G_<1 data-lazy-src= ,G_\ldots G_»/>, причем вершин, $i=1\ldots k$ . Каждая компонента является деревом, поэтому, как доказано выше, число ребер в равно n_-1 , а всего ребер в графе $\suml_<i=1 data-lazy-src=$ ^\left(n_ -1\right) =n-k=n-1″/>. Значит, $\Rightarrow$ (2). Рассмотрим связный граф с n-1 ребром. Если бы в нем был цикл, то, удалив любое цикловое ребро, мы получили бы связный граф с меньшим числом ребер. Можно продолжать такое удаление ребер до тех пор, пока не останется связный граф без циклов, то есть дерево. Но ребер в этом дереве было бы меньше, чем n-1 , а это противоречит доказанному выше.

Теорема 2. Если — дерево, то

в любая пара вершин соединена единственным путем;
при добавлении к любого нового ребра образуется цикл;
при удалении из любого ребра он превращается в несвязный граф .

Существование пути между любыми двумя вершинами следует из связности дерева. Допустим, что в некотором дереве существуют два различных пути, соединяющих вершины и . Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той же вершине ). Пусть — последняя вершина этого совпадающего начала, а после в одном пути следует вершина y_<1 data-lazy-src= »/>, а в другом — вершина $\left(x,y_<1 data-lazy-src=$ \right)»/>. Если его удалить из графа, то в оставшемся подграфе вершины будут соединимыми — соединяющий их маршрут можно построить так: взять отрезок первого пути от y_<1 data-lazy-src= »/> до до , взятый в обратном порядке. Но это означает, что ребро $\left(x,y_<1 data-lazy-src=$ \right)»/> не является перешейком. Однако из теоремы 4 «Маршруты, связность, расстояния» следует, что в дереве каждое ребро является перешейком. Этим доказано утверждение 1). Утверждения 2) и 3) следуют из 1).

Отметим, что единственный путь , соединяющий две вершины дерева, всегда простой (если путь не является простым, в нем обязательно содержится цикл).

Источник