3. Деревья
Полезной нелинейной структурой данных является дерево (или лес).
3.1. Определения дерева, леса, бинарного дерева. Скобочное представление
Дадим формальное определение дерева, следуя [10].
Дерево – конечное множество Т, состоящее из одного или более узлов, таких, что
а) имеется один специально обозначенный узел, называемый корнем данного дерева;
б) остальные узлы (исключая корень) содержатся в m 0 попарно не пересекающихся множествах Т1, Т2, . Тm, каждое из которых, в свою очередь, является деревом. Деревья Т1, Т2, . Тm называются поддеревьями данного дерева.
При программировании и разработке вычислительных алгоритмов удобно использовать именно такое рекурсивное определение, поскольку рекурсивность является естественной характеристикой этой структуры данных.
Каждый узел дерева является корнем некоторого поддерева. В том случае, когда множество поддеревьев такого корня пусто, этот узел называется концевым узлом, или листом. Уровень узла определяется рекурсивно следующим образом: 1) корень имеет уровень 1; 2) другие узлы имеют уровень, на единицу больший их уровня в содержащем их поддереве этого корня. Используя для уровня узла а дерева T обозначение уровень (a, T), можно записать это определение в виде
где Ti – поддерево корня дерева T, такое, что a Ti.
Говорят, что каждый корень является отцом корней своих поддеревьев и что последние являются сыновьями своего отца и братьями между собой. Говорят также, что узел n – предок узла m (а узел m – потомок узла n), если n – либо отец m, либо отец некоторого предка m.
Если в определении дерева существен порядок перечисления поддеревьев Т1, Т2, . Тm, то дерево называют упорядоченным и говорят о «первом» (Т1), «втором» (Т2) и т. д. поддеревьях данного корня. Далее будем считать, что все рассматриваемые деревья являются упорядоченными, если явно не оговорено противное. Отметим также, что в терминологии теории графов определенное ранее упорядоченное дерево более полно называлось бы «конечным ориентированным (корневым) упорядоченным деревом».
Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть может, равного нулю) числа непересекающихся деревьев. Используя понятие леса, пункт б в определении дерева можно было бы сформулировать так: узлы дерева, за исключением корня, образуют лес.
Традиционно дерево изображают графически, например так, как на рис. 3.1.
Error: Reference source not foundРис. 3.1. Графическое изображение дерева
В графическом представлении для изображения структуры дерева используется двухмерность рисунка. При машинной обработке часто удобнее использовать текстовое представление дерева. Например, таким представлением может быть так называемый уступчатый список. Здесь «двухмерность» проявляется за счет того, что текст разбит на строки и фиксируется позиция символа узла в строке. На рис. 3.2, а, б представлено в виде уступчатого списка дерево, изображенное на рис. 3.1.
Другой вид текстового (и принципиально одномерного) представления дерева это так называемая скобочная запись (ср. с записью иерархических списков в 1.7). Определим скобочное представление дерева и леса:
a ▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓ а b i b ▓▓▓▓▓▓▓▓▓▓▓▓▓▓
i ▓▓▓▓▓▓▓▓▓▓ j j ▓▓▓▓▓▓▓▓▓▓ c ▓▓▓▓▓▓▓▓▓▓▓▓▓▓ c h h ▓▓▓▓▓▓▓▓▓▓ d ▓▓▓▓▓▓▓▓▓▓▓▓▓▓ d e e ▓▓▓▓▓▓▓▓▓▓ f ▓▓▓▓▓▓▓▓▓▓ f k k ▓▓▓▓▓▓▓ g ▓▓▓▓▓▓▓▓▓▓ g
Рис. 3.2. Представление дерева: а – в виде уступчатого списка; б – в виде «упрощенного» уступчатого списка
В скобочном представлении дерево, изображенное на рис. 3.1, запишется как
(a (b (i) (j)) (c (h)) (d (e) (f (k)) (g))).
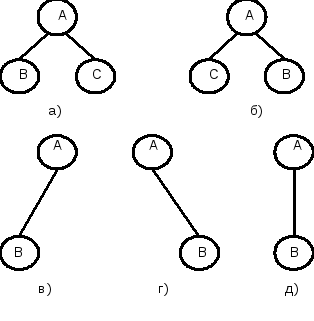
Наиболее важным типом деревьев являются бинарные деревья. Удобно дать следующее формальное определение. Бинарное дерево конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев, называемых правым поддеревом и левым поддеревом. Так определенное бинарное дерево не является частным случаем дерева. Например, бинарные деревья, изображенные на рис. 3.3, различны между собой, так как в одном случае корень имеет пустое правое поддерево, а в другом случае правое поддерево непусто. Если же их рассматривать как деревья, то они идентичны.
Рис. 3.3. Бинарные деревья из двух узлов
Определим скобочное представление бинарного дерева (БД):
Здесь пустое дерево имеет специальное обозначение .
Например, бинарное дерево, изображенное на рис. 3.4, имеет скобочное представление
(a (b (d Λ (h Λ Λ)) (e Λ Λ)) (c (f (i Λ Λ) (j Λ Λ)) (g Λ (k (l Λ Λ) Λ)))).
Error: Reference source not foundError: Reference source not foundРис. 3.4. Бинарное дерево
Можно упростить скобочную запись бинарного дерева, исключив «лишние» знаки по правилам:
Тогда, например, скобочная запись бинарного дерева, изображенного на рис. 3.4, будет иметь вид
(a (b (d (h) (e)) (c (f (i) (j)) (g (k (l))))).
Источник
30. Бинарные деревья.
Существуют m-арные деревья, т.е. такие деревья у которых полустепень исхода каждой вершины меньше или равна m (где m может быть равно 0,1,2,3 и т.д.). Если полустепень исхода каждой вершины в точности равна либо m, либо нулю, то такое дерево называется ПОЛНЫМ m-АРНЫМ ДЕРЕВОМ.
При m=2 такие деревья называются соответственно БИНАРНЫМИ, или ПОЛНЫМИ БИНАРНЫМИ.
На рисунке 6.12(a) изображено бинарное дерево, 6.12(b)- полное бинарное дерево, а на 6.12(c) показаны все четыре возможных расположения сыновей некоторой вершины бинарного дерева.
Рис. 6.13. Изображения бинарных деревьев
В позиционном бинарном дереве каждая вершина представлена единственным образом посредством строки символов над алфавитом , при этом корень характеризуется пустой строкой. Любой сын вершины «u» характеризуется строкой, префикс (начальная часть) которой является строкой, характеризующей «u». Примером бинарного дерева является фамильное дерево с отцом и матерью человека в качестве его потомков. Еще один пример — это арифметическое выражение с двухместными операциями, где каждая операция представляет собой ветвящийся узел с операндами в качестве поддеревьев.
Представление любого дерева, леса бинарными деревьями. Дерево и лес любого вида можно преобразовать единственным образом в эквивалентное бинарное дерево.
Правило построения бинарного дерева из любого дерева:
- 1. В каждом узле оставить только ветвь к старшему сыну (вертикальное соединение);
- 2. Соединить горизонтальными ребрами всех братьев одного отца;
- 3. Таким образом перестроить дерево по правилу:
- левый сын — вершина, расположенная под данной;
- правый сын — вершина, расположенная справа от данной (т.е. на одном ярусе с ней).
- 4. Развернуть дерево таким образом, чтобы все вертикальные ветви отображали левых сыновей, а горизонтальные — правых.
В результате преобразования любого дерева в бинарное получается дерево в виде левого поддерева, подвешенного к корневой вершине. В процессе преобразования правый указатель каждого узла бинарного дерева будет указывать на соседа по уровню. Если такового нет, то правый указатель NIL. Левый указатель будет указывать на вершину следующего уровня. Если таковой нет, то указатель устанавливается на NIL. 
Рис.6.14. Исходное дерево
Рис.6.15 Промежуточный результат перестройки дерева
Рис. 6.16. Представление дерева в виде бинарного Описанный выше метод представления произвольных упорядоченных деревьев посредством бинарных деревьев можно обобщить на представление произвольного упорядоченного леса. Правило построения бинарного дерева из леса: корни всех поддеревьев леса соединить горизонтальными связями. В полученном дереве узлы в данном примере будут располагаться на трех уровнях. Далее перестраивать по ранее рассмотренному плану: в начале поддерево с корнем А, затем В и затем Н. В результате преобразования упорядоченного леса в бинарное дерево получается полное бинарное дерево с левым и правым поддеревом. Машинное представление деревьев в памяти ЭВМ. Деревья можно представлять с помощью связных списков и массивов (или последовательных списков). Чаще всего используется связное представление деревьев, т.к. оно очень сильно напоминает логическое. Связное хранение состоит в том, что задается связь от отца к сыновьям. В бинарном дереве имеется два указателя, поэтому удобно узел представить в виде структуры:
| LPTR | DATA | RPTR |
где LPTR — указатель на левое поддерево, RPTR — указатель на правое поддерево, DATA — содержит информацию, связанную с вершиной.
Источник
1.3.4. Деревья и их представление
Конечное корневоедерево T формально определяется как непустое множество упорядоченных узлов, таких что существует один выделенный узел, называемыйкорнемдерева, а оставшиеся узлы разбиты на m>=0 поддеревьев Т1,Т2. Тm. Узлы, не имеющие поддеревьев, называютсялистьями; остальные узлы называются внутренними узлами.
Рис.3.8. Дерево с 11 узлами, помеченными буквами от А до К. Узлы с метками D,E,F,H,J и K являются листьями; другие узлы внутренние. Узел А — корень.
Посредством деревьев изображаются иерархические организации, поэтому они являются нелинейными структурами данных в комбинаторных алгоритмах.
В описанных соотношениях между узлами дерева мы используем терминологию, принятую в генеалогических деревьях. Так, мы говорим, что в дереве (или поддереве) все узлы являются потомками его корня, и наоборот, корень — предок всех своих потомков. Корень именуется отцом корней его поддеревьев, которые в свою очередь будут сыновьями корня. Например, на рис. 3.8 узел А является отцом узлов B,G и I; J и K — сыновья I, а C, E, F -братья.
Все рассматриваемые нами деревья будут упорядочены, т.е. для них будет важен относительный порядок расположения каждого узла. Таким образом, деревья считаются различными.
Определим лес как упорядоченное множество деревьев; в связи с этим мы можем перефразировать определение дерева: дерево есть непустое множество узлов, такое, что существует один выделенный узел, называемый корнем дерева, а оставшиеся узлы образуют лес с m>=0 поддеревьями корня.
Важной разновидностью корневых деревьев является класс бинарных деревьев. Бинарное дерево Т либо пустое, либо состоит из выделенного узла, называемого корнем, и двух бинарных поддеревьев: левого Тlи правого Tr. Бинарные деревья, вообще говоря не являются подмножеством множества деревьев, они полностью отличаются по своей структуре, поскольку две следующие картинки ( а) и б)) не изображают одно и то же бинарное дерево. Как деревья, однако, они обе неотличимы от ( в) ).
Различие между деревом и бинарным деревом состоит в том, что дерево не может быть пустым, и каждый узел дерева может иметь произвольное число поддеревьев; в тоже время бинарное дерево может быть пустым, каждая из его вершин может иметь 0, 1 или 2 поддерева, и существует различие между левыми и правыми поддеревьями.
Почти все машинное представления деревьев основаны на связанных распределениях. Каждый узел состоит из поля INFO и некоторых полей для указателей. Например, одно из представлений для каждого узла имеет единственное поле для указателя F (FATHER), указывающее на отца данного узла. При этом приведенное на рис.3.8 дерево будет выглядеть так, как показано на рис.310.
Рис.3.10.Дерево из рис.3.8, представленное из узлов с полем INFO и указателем FATHER.
Такое представление полезно, если необходимо подниматься по дереву от потомков к предкам. Такая операция встречается довольно редко; чаще требуется опуститься по дереву от предков к потомкам.
Представление дерева (или леса) с использованием указателей, ведущих от предков к потомкам, довольно сложно, поскольку узел, имея не более одного отца, может иметь в тоже время произвольно много сыновей. Другими словами, при таком представлении узлы должны различаться по размеру, что является определенным неудобством. Один из путей обхода этой трудности состоит в том, чтобы определить соотношение между деревьями и бинарными деревьями, поскольку бинарные деревья легко представить узлами фиксированного размера. Каждый узел в этом случае имеет три поля: LEFT (указывает положение корня левого поддерева), INFO (содержимое узла) и RIGHT (указатель местоположения корня правого поддерева). Все сказанное выше проиллюстри-ровано на рис.3.11.
а) б)
Рис.3.11. Бинарное дерево (а) и его представление (б) с помощью узлов с тремя
полями LEFT , INFO и RIGTH.
Мы можем представлять деревья как бинарные деревья ( используя узлы фиксированного размера), представляя каждый узел леса в виде узла, состоящего из полей LEFT, INFO и RIGHT. При этом поле LEFT предназначается для указания самого левого сына
данного узла, а поле RIGHT — для указания следующего брата данного узла. Например, лес (рис.3.11,а) преобразуется в бинарное дерево ( рис.3.11,б). Таким образом, мы используем поле LEFT некоторого узла для указателя на связанный список сыновей этого узла; этот список связывается с помощью полей RIGHT. Такое представление мы будем называть естественным соответствием между лесами и бинарными деревьями.
а)
Рис.3.12. Лес (а) и его представление в виде бинарного дерева (б)
Двоичное дерево обычно представляют в виде двух массивов LES (LEFTSON-левый сын) и RIS (RIGHTSON-правый сын). Пусть узлы двоичного дерева занумерованы целыми числами от 1 до N. В этом случае LES[i]=j узел с номером j является левым сыном узла с номером i. Если у узла i нет левого сына, то LES[i]=0. RES[i] определяется аналогично.
Источник