Минимальные остовные деревья нагруженных графов
Граф G = (X, A) называется нагруженным, если для каждого ребра (xi, xj) определена его длина (или вес) cij.
Пусть G — связный нагруженный граф. Задача построения минимального остовного дерева заключается в том, чтобы из множества остовных деревьев найти дерево, у которого сумма длин ребер минимальна.
Приведем типичные случаи, когда возникает необходимость построения минимального остовного дерева графа.
а) Нужно соединить n городов железнодорожными линиями (автомобильными дорогами, линиями электропередач, сетью трубопроводов и т.д.) так, чтобы суммарная длина линий или стоимость была бы минимальной.
б)Требуется построить схему электрической сети, в которой клеммы должны быть соединены с помощью проводов наименьшей общей длины.
Задачу построения минимального остовного дерева можно решить с помощью следующего алгоритма.
Алгоритм 3.2 (Алгоритм Краскала).
Шаг 1. Установка начальных значений.
Вводится матрица длин ребер C графа G.
Шаг 2. Выбрать в графе G ребро минимальной длины. Построить граф G 2, состоящий из данного ребра и инцидентных ему вершин. Положить i = 2.
Шаг 3. Если i = n, где n — число ребер графа, то закончить работу (задача решена), в противном случае перейти к шагу 4.
Шаг 4. Построить граф Gi + 1, добавляя к графу Gi новое ребро минимальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно какой-нибудь вершине графа Gi и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в Gi. Вместе с этим ребром включаем в Gi + 1и инцидентную ему вершину, не содержащуюся в Gi. Присваиваем i: = i +1 и переходим к шагу 3.
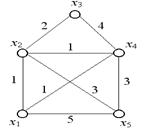
Найдем минимальное остовное дерево для графа, изображенного на рис. 3.14.
Шаг 1. Установка начальных значений.
Введем матрицу длин ребер C:
Шаг 2. Выберем ребро минимальной длины. Минимальная длина ребра равна единице. Таких ребер три: (x 1, x 2), (x 1, x 4), (x 2, x 4). В этом случае можно взять любое. Возьмем (x 1, x 2). Построим граф G 2, состоящий из данного ребра и инцидентных ему вершин x 1 и x 2. Положим i = 2.
Шаг 3. Так как n = 5, то i ¹ n, поэтому переходим к шагу 4.
Шаг 4. Строим граф G 3, добавляя к графу G 2новое ребро минимальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно одной из вершин x 1, x 2 и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в G 2 т. е. одной из вершин x 3, x 4, x 5. Таким образом, нужно выбрать ребро минимальной длины из ребер (x 1, x 4), (x 1, x 5), (x 2, x 3), (x 2, x 4), (x 2, x 5). Таких ребер длины единица два: (x 1, x 4) и (x 2, x 4). Можно выбрать любое. Возьмем (x 1, x 4). Вместе с этим ребром включаем в G 3вершину x 4, не содержащуюся в G 2. Полагаем i =3 и переходим к шагу 3.
Шаг 3. Так как i ¹ n, поэтому переходим к шагу 4.
Шаг 4. Строим граф G 4, добавляя к графу G 3новое ребро минимальной длины из ребер (x 1, x 5), (x 2, x 3), (x 2, x 5), (x 4, x 5). Такое ребро длины два одно: (x 2, x 3). Вместе с этим ребром включаем в G 4вершину x 3, не содержащуюся в G 3. Полагаем i =4 и переходим к шагу 3.
Шаг 3. Так как i ¹ n, поэтому переходим к шагу 4.
Шаг 4. Строим граф G 5, добавляя к графу G 3новое ребро минимальной длины из ребер (x 1, x 5), (x 2, x 5), (x 4, x 5). Таких ребер длины три два: (x 2, x 5) и (x 4, x 5). Возьмем (x 2, x 5). Вместе с этим ребром включаем в G 5вершину x 5, не содержащуюся в G 4. Полагаем i =5 и переходим к шагу 3.
Шаг 3. Так как i = n, то граф G 5 – искомое минимальное остовное дерево. Суммарная длина ребер равна 1 + 1 + 2 + 3 = 7.
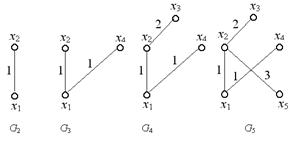
Процесс построения минимального остовного дерева изображен на рис. 3.15.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
Лабораторная работа №2.
Цель работы: ознакомиться с алгоритмами нахождения минимального остового дерева нагруженного графа, поиска маршрута с минимальным числом ребер в ориентированном графе, нахождения минимального пути в нагруженном графе.
Теоретические сведения
Остовное дерево связного графа
Остовным деревом связного графа G называется любая его часть, содержащая все вершины графа G и являющаяся деревом.
Минимальные остовные деревья нагруженных графов
Граф G(V.E) называется нагруженным, если на множестве его ребер определена весовая функция l:Е→R, т.е. каждому ребру е Е связного графа G=(V,E) с непустым множеством ребер Е поставлена в соответствие величина l(е) — длина ребра е. Приведем алгоритм, позволяющий найти остовное дерево графа G с минимальной суммой длин содержащихся в нем ребер (по сравнению со всеми другими остовными деревьями графа G). Остовное дерево связного нагруженного графа G с минимальной суммой длин содержащихся в нем ребер будем называть минимальным остовным деревом (МОД) графа G.
Алгоритм выделения МОД нагруженного связного графа G:
Шаг 1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему вершинами оно образует часть графа G2 графа G. Положим i=2.
Шаг 2. Если i=n, где n=n(G), то задача решена, и G, — искомое МОД графа G. В противном случае переходим к шагу 3.
Шаг 3. Строим граф Gi+1, добавляя к графу G, новое ребро минимальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно какой-нибудь вершине графа G, и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся Gi. Вместе с этим ребром включаем в Gi+1 и инцидентную ему вершину, не содержащуюся в Gi. Присваиваем i:=i+l и переходим к шагу 2.
Поиск путей (маршрутов) с минимальным числом дуг (ребер)
Пусть в орграфе D из вершины v в вершину w, где v≠w, называется минимальным, если он имеет минимальную длину среди всех путей орграфа D из v в w.
Назовем образом вершины х в орграфе D множество концов дуг, началом которых является вершина х, и обозначим его D(x). Множество начал дуг, концом которых является х, назовем прообразом х и обозначим его D -1 (x)
Пусть D=(V,X) — орграф с n вершинами (n≥2) и v,w — заданные вершины из V, где v≠w. Опишем алгоритм поиска минимального пути из v в w в орграфе D (алгоритм фронта волн).
Шаг 1. Помечаем вершину v индексом 0. Затем помечаем вершины, принадлежащие образу вершины v, индексом 1. Множество вершин с индексом 1 обозначаем FW1(v). Полагаем k=l.
Шаг 2. Если FWk(v)=0 или выполняется k=n-l и w FWk(v), то вершина w не достижима из v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.
Шаг 3. Если w FWk(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k, и этот путь является минимальным. Последовательность вершин:
и есть искомый минимальный путь из v в w. На этом работа алгоритма заканчивается.
Шаг 4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k+1 обозначаем FWk+1(v). Присваиваем k=k+l и переходим к шагу 2.
Множество FWk(v) в данном алгоритме обычно называют фронтом волны k- го уровня.
Вершины wb. ., wk_i из (9.10), вообще говоря могут быть выделены неоднозначно. Эта неоднозначность соответствует случаям, когда существует несколько различных минимальных путей из v в w в орграфе D.
Пример. Определим минимальный путь v1 в v6 в орграфе D, заданном матрицей смежности, представленной в таблице.
Источник
3.3.3. Минимальные остовные деревья нагруженных графов
Пусть теперь каждому ребру x X связного графа G=(V,X) c непустым множеством ребер Х поставлена в соответствие величина l(x) – длина ребра х, т.е. граф G является нагруженным. Приведем алгоритм, позволяющий найти остовное дерево графа G с минимальной суммой длин содержащихся в нем ребер (по сравнению со всеми другими остовными деревьями графа G).
Определение. Остовное дерево связного нагруженного граф G с минимальной суммой длин содержащихся в нем ребер будем называть минимальным остовным деревом (МОД) графа G.
Алгоритм выделения МОД нагруженного связного графа G:
Шаг 1. Выберем в графе G ребро минимальной длины. Вместе с инцидентными ему вершинами оно образует подграф G2 графа G. Положим i=2.
Шаг 2. Если i=n, где n=n(G), то задача решена, и Gi – искомое МОД графа G. В противном случае переходим к шагу 3.
Шаг 3. Строим граф Gi+1, добавляя к графу Gi новое ребро минимальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно к какой-нибудь вершине графа Gi и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в Gi. Вместе с этим ребром включаем в Gi+1 и инцидентные ему вершины, не содержащиеся в Gi . Присваиваем i:=i+1 и переходим к шагу 2.
Определить МОД нагруженного графа G, изображенного на рис. 3.23, используя алгоритм.
Рис. 3.23. Граф для примера 89
На рис. 3.23 приведена последовательность графов Gi, i=2,3,4,5, получаемых в результате выполнения алгоритма. При этом в силу того, что n(G)=5, G5 — МОД графа G. Причем, МОД(G) = 7.
Замечание. Возможно выделить в графе несколько остовных деревьев, каждое из которых будет являться минимальным, при этом величина МОД для всех этих деревьев будет равной.
Замечание. Для выделения МОД нагруженного псевдографа G следует предварительно удалить из G петли, из кратных ребер оставить лишь ребра минимальной длины.
Рис. 3.23. Последовательность графов для примера 89
Источник