Оценка объектов по многоуровневой системе критериев
Как указывалось ранее, в практических задачах число критериев может достигать нескольких десятков. Применять функции полезности и проверять различные свойства типа независимости по полезности или по предпочтению даже для пяти-шести критериев крайне затруднительно. Поэтому множество критериев необходимо структуризовать в виде дерева критериев, а затем проводить агрегирование критериев по дереву. Данный подход по этапам рассматривается в этом разделе.
Построение дерева критериев
Множество единичных критериев необходимо сгруппировать и структуризовать в виде дерева критериев. Как правило, дерево содержит от трех до шести уровней.
Самый нижний уровень образуют единичныекритерии. Критерий второго и последующих уровней называютсякомплексными, критерий самого верхнего уровня (корень дерева) называетсяинтегральнымилиобобщенным, но его можно рассматривать как один из комплексных критериев.
Таким образом, все критерии классифицируются на два типа:
Принципиальное отличие комплексных критериев от единичных заключаются в их измерении. Единичные измеряются в физических единицах, их значения являются основой для определения всех комплексных. Все комплексные критерии измеряются в относительных единицах в интервале от нуля до единицы. Значения, близкие к нулю, указывают на низкую полезность объекта по данному комплексному критерию и, наоборот, значения, близкие к единице, –на высокую полезность.
Дерево критериев отражает перечень единичных и комплексных критериев и их логическую взаимосвязь. Для интегральной оценки объектов дерево должно быть дополнено функциональными связями между единичными и комплексными критериями, т.е. должны быть заданы операторы агрегирования всех комплексных показателей по дереву и указана вся необходимая для агрегирования информация. Следовательно, задача оценки вариантов по многоуровневой системе критериев включает решение следующих вопросов:
построения дерева критериев;
перехода от различных физических единиц измерения единичных критериев к относительным величинам;
задания операторов агрегирования критериев по дереву.
При построении дерева критериев единичные и комплексные критерии идентифицируются индексами, определяющими их положение в структуре.
Переход от физических единиц измерения критериев к относительным осуществляется с использованием функций перевода.
Следует отметить, что для оценки объектов целесообразно с использованием одного множества единичных критериев разработать несколько деревьев, т.е. провести несколько структуризаций критериев. После чего сделать оценку объектов по каждому дереву и провести сравнительный анализ результатов с целью выбора варианта, обеспечивающего наиболее устойчивые результаты.
Функции перевода
Как указывалось ранее, переход от физических единиц измерения к относительным осуществляется с помощью функций перевода uj(kj). Далее в данном разделе индекс единичного критерия в функции переводаu(k) будем опускать.
Отличительными особенностями функций перевода являются:
значения функций изменяются в интервале от нуля до единицы;
имеется рабочий интервал аргумента от kminдоkmax, вне которого функция принимает постоянные значения. Нижняя и верхняя границы измерения аргумента определяют требования к объекту по рассматриваемому критерию.
Таким образом, для задания функции перевода необходимо задать ее вид и параметры, среди которых обязательными являются нижняя и верхняя границы.
Несмотря на многообразие функций перевода, можно привести несколько типовых функций, которые отражают большинство случаев, встречающихся в практике решения многокритериальных задач.
Монотонные функции перевода. Рассмотрим сначала возрастающие монотонные функции перевода. Эти функции используются для перехода к относительным единицам измерения по критериям, при увеличении которых предпочтение объектов возрастает.
Линейная функция переводаопределяется в соответствии с выражением
u(k) = (k — kmin) / (k — kmax)приk[kmin; kmax];u(k) = 0 приk ≤ kmin;u(k) = 1 приk ≥ kmax .
Линейная функция используется для перехода к относительным величинам, когда приращение полезности критерия не зависит от его значений, т.е. если увеличить аргумент на Δk, то приращение полезностиΔu(k)будет одинаковым при разныхk.
Кусочно-линейная функция переводаразбивает область измененияu(k)на два интервала, скорость изменения на каждом из которых разная. Данная функция перевода применяется, когда требуется указать, что возрастание единичного критерия на интервалеkminдо порогового значенияkПболее существенно, чем на интервале отkПдоkmax.
Гауссовской функции переводасоответствует функция вероятности нормального закона распределения. Поскольку область определения функции не ограничена, то при ее использовании в качестве функции перевода в программном обеспеченииF(kmin)=0.01; F(kmin)=0.99. Из этих условий определяется σдля функцииF(k). Используется гауссовская функция перевода в тех случаях, когда изменения единичного критерия в областях, близких к нижней и верхней границам, несущественны.
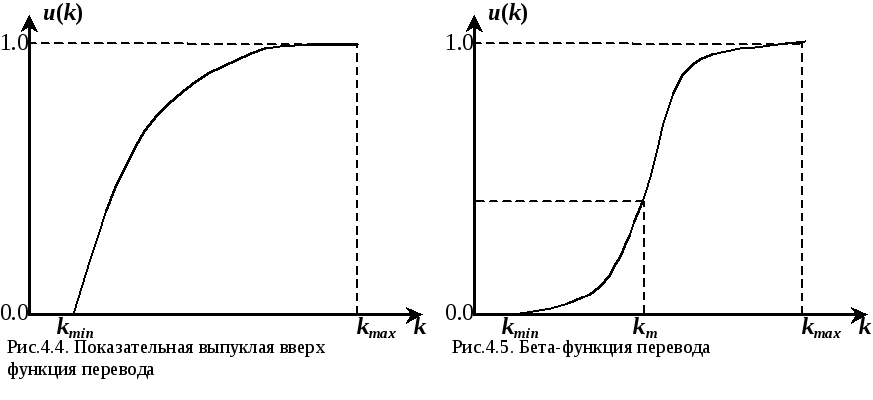
Показательная функция перевода. Различаются два вида возрастающих показательных функций перевода.Показательная выпуклая вверх функция переводаопределяется в соответствии с выражением: приk[kmin; kmax], a(0;1); u(k) = 0 приk kmin;u(k) = 1 приk > kmax .
Данная функция используется в тех случаях, когда весьма существенны значения критерия, близкие к нижней границе, и критерий не влияет на полезность объектов при дальнейшем его увеличении до верхней границы.
Показательная выпуклая вниз функция перевода применяется, когда на начальном участке изменение критерия несущественно влияет на полезность объектов и резко увеличивается полезность близ верхней границы.
Показательная выпуклая вниз функция перевода определяется по той же формуле, что и показательная выпуклая вверх, но при основании aбольше единицы. Параметрами показательных функций перевода являются нижняя и верхняя границы, а также основание.
Бета-функция переводасоответствует функции вероятности закона бета-распределения
при k[kmin; kmax],
где C – коэффициент, вычисленный из условияu(kmax)=1; u(k)=0 приk ≤ kmin;u(k)=1 приk ≥ kmax.
Параметры vиqвлияют на точку перегиба (моду – km) и степень отклонения функции от линейной функции (крутизну).
Для задания бета-функции перевода необходимо указать значение моды km, соответствующее точке перегиба, и суммуs = v + q, характеризующую крутизну.
Особенностью данной функции перевода является ее несимметричность, что позволяет задавать с ее помощью широкий круг требований при изменении единичных критериев.
При переводе в относительные величины критериев, при увеличении которых уменьшается предпочтение объектов, следует использовать убывающие монотонные функции перевода.
Монотонные убывающие функции перевода u′(k)вычисляются на основе возрастающих функций в соответствии свыражениемu′(k) = 1 — u(k).
Виды убывающих функций перевода те же, что и возрастающих.
Немонотонные функции перевода.Данный класс функций используется, когда существует оптимальное значение критерия, а отклонение от него в сторону увеличения или уменьшения рассматривается как снижение полезности.
Функция перевода плотности бета-распределенияопределяется в соответствии с выражениями
u(k) = d∙(k — kmin) v (kmax— k) q приk[kmin; kmax];u(k) = 0 приk ≤ kmin иk ≥ kmax ,
где коэффициент d вычисляется из условия, чтобы максимальное значениеu(k)в интервале[kmin;kmax]равнялось единице, т.е.u(km) = l. Положение максимума функции определяет параметрkm, соответствующий моде бета-распределения, а крутизну функции –параметрs = v + q.
Функция перевода плотности бета-распределения с насыщениемотличается от вышерассмотренной функции тем, что приk > kmaxона принимает заданное значение u(kmax). Такого вида функции перевода используются в тех случаях, когда большое превышение оптимального значения критерия не рассматривается как существенное уменьшение полезности. Для задания данной функции перевода необходимо указать: нижнюю и верхнюю границы, модуkm, величинуs = v + qи значениеu(kmax).
Источник
Определение и свойства деревьев.
Деревом называется произвольный связный граф без циклов. Деревья обладают следующими свойствами:
любые две вершины соединены единственной простои цепью
количество ребер на единицу меньше количества вершин
при удалении любого ребра дерево становится не связным графом
при добавлении к дереву любого ребра в дереве появляется ровно один простой цикл.
Фактически дерево можно получить из любого связного графа
Утверждение: любой связный граф содержит остовный подграф который является деревом. Этот подграф называется остовыным деревом.
Специальные виды деревьев
1 Корневые деревья
Определение: Корневое дерево — ориентированное дерево, которое удовлетворяет условиям:
a) Имеется ровно один узел в который не входит не одно
В каждый узел кроме корня входит ровно одно ребро
Из корня имеется путь к любому ребру.
Если имеется путь от вершины vl к вершине v2, тогда вершина vl предок вершины v2, а вершина v2 потомок вершины vl.
Вершина которая не имеет потомков называется концевой вершиной или листом. Не концевую вершину называют внутренней. Если V1 и V2 дуга корневого дерева, то V1— отец, a V2— сын
Глубина дерева — длина пути из корня. Узлы находящиеся на одной глубине называются ярусами дерева.
Для задания корневого дерева можно использовать те же способы, что и для любого графа. На практике для представления деревьев используется канонический способ: для каждого узла хранится указатель на отца.
2 Бинарные деревья
Определение: Бинарное дерево — корневое дерево у каждой вершины которого не более двух сыновей.
В таком дереве любой произвольный узел имеет левого и правого сына. Поддерево корнем которого является левый сын называется левым поддеревом. Поддерево корнем которого является правый сын называется правым поддеревом.
Имеется два способа представления бинарных деревьев:
1. Представление в виде двух массивов: первый массив- левые сыновья, второй — правые.
2. Представление в виде списковой структуры tree_ ptr Tree_mode — запись имеющая структуру:
Element- тип узла; Left: tree_ ptr; Right: tree_ ptr;
3 Полные бинарные деревья
Определение: Полное бинарное дерево — бинарное дерево для которого выполняются условия:
a) Заполнение дерева осуществляется от корня к листьям по уровням.
b) Заполнение уровней осуществляется слева направо.
Полные бинарные деревья представляются в виде одномерного массива: первый элемент массива — корень дерева. Для любого i-того узла элемент с индексом (2i) — левый сын, элемент с индексом (2i+l)- правый сын. Отец узла j — (j/2).
4 Бинарные поисковые деревья
Определение: Бинарное поисковое дерево — дерево поиска,
Все ключи в левом поддереве меньше ключа узла V
В правом поддереве все ключи больше, чем ключ V
В дереве нет одинаковых ключей.
5 Сбалансированные деревья
Определение: Дерево называется идеально сбалансированным, если оно является бинарным поисковым деревом и число вершин его левых и правых поддеревьев отличается не более, чем на единицу.
Определение: Дерево называется сбалансированным, если оно бинарное поисковое и высоты двух поддеревьев в каждой из вершин отличаются не более, чем на единицу.
6 Способы обхода узлов в бинарных деревьях
Большинство алгоритмов при работе с деревьями посещают каждый узел в некотором порядке.
Существует три наиболее распространенных способа обхода деревьев:
1. Прямой порядок: корень посещается раньше, чем поддеревья
Порядок обхода: корень — левое поддерево — правое поддерево.
Процедура организуется рекурсивно.
2. Обратный порядок (снизу вверх): корень посещается после поддеревьев.
Порядок обхода: левое поддерево — правое поддерево- корень.
3. Внутренний порядок (слева направо )
Порядок обхода: левое поддерево – корень — правое поддерево.
7 Представление множеств с помощью деревьев
Базовыми операциями над множествами являются:
определение принадлежности элемента множества.
объединение не пересекающихся множеств.
Каждое множество будем представлять в виде корневого дерева. Корень дерева можно использовать для хранения имени множества. Дерево будем представлять в каноническом виде.
Чтобы определить, к какому множеству принадлежит некоторый элемент — находим этот элемент и определяем корень множества, к которому он принадлежит. Этот корень — есть имя искомого множества.
Объединение непересекающихся множеств можем реализовать тремя способами:
Источник