Деревья ориентированные деревья бинарные деревья

4.2. Ориентированные, упорядоченные и бинарные деревья

Ориентированным деревом (ордеревом, корневым деревом) называется орграф со следующими свойствами.

1. Существует единственная вершина, полустепень захода которой равна 0. Она называется корнем ориентированного дерева.
2. Полустепень захода всех остальных вершин равна 1.
3. Каждая вершина достижима из корня.

а) все возможные ориентированные деревья с 3-я вершинами:

Концевая (висячая) вершина ордерева называется листом. Путь из корня в лист называется ветвью.

Уровень вершины ордерева – это расстояние от корня до вершины. Корень имеет уровень 0. Вершины одного уровня образуют ярус дерева.

Эквивалентное определение ориентированного дерева

Ордерево D – это конечное множество вершин, таких что:

1) имеется одна вершина r, называемая корнем данного дерева;

2) остальные вершины содержаться в k попарно непересекающихся множества D₁,…D_k , каждое из которых является ордеревом. (k0) D= .

Множества D₁,…,D_k называются поддеревьями.

Упорядоченным деревом называется ориентированное дерево, в котором:

1. задан порядок поддеревьев
2. каждое поддерево D_i является упорядоченным поддеревом.
3. дерево с одной вершиной считается упорядоченным поддеревом.

Замечание. При изображении ориентированных деревьев принято соглашение о том, что корень размещается вверху. В связи с этим все дуги оказываются ориентированными сверху вниз, поэтому стрелки на них можно не изображать. В результате, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми. В этом случае требуется дополнительное указание, какого класса дерево изображено на диаграмме. Обычно это ясно из контекста.

Н апример: Имеются 3 диаграммы деревьев:

Как упорядоченные деревья, они все различны. Как ориентированные деревья D₁=D₂D₃. Как свободные деревья, они все изоморфны D₁=D₂=D₃.

Терема 3. Число упорядоченных деревьев с m дугами не превосходит 4 m .

Доказательство: Рассмотрим алгоритм обхода упорядоченного дерева, называемого «поиском в глубину». Этот обход рекурсивно описывается следующим образом:

1. Начать с корня. Пока есть деревья выполнять.
2. Перейти в корень очередного поддерева, обойти это поддерево в глубину.
3. Вернуться в корень исходного поддерева.

В результате «обхода в глубину» по каждой дуге проходят ровно 2 раза: один раз при переходе в очередное поддерево, второй раз – при возвращении из него. В соответствии с «обходом в глубину» строиться последовательность из нулей и единиц. На каждом шаге записывается нуль, если происходит переход в очередное поддерево, а единица – при возвращении из поддерева. В результате получается последовательность из нулей и единиц длины 2m, которая называется кодом дерева. По этому коду однозначно восстанавливается дерево, т.к. каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус

ближе к корню. Таким образом. упорядоченных деревьев с m дугами не больше, чем последовательностей из нулей и единиц длины 2m. А их число равно 2 2 m =4 m . Теорема доказана.

Изоморфизм ориентированных деревьев определяется так же, как и изоморфизм графов, но с дополнительным условием — корень должен отображаться в корень. Для упорядоченных деревьев требуется также сохранение порядка поддеревьев.

Следствие. Число неизоморфных ориентированных или свободных деревьев с m ребрами не превосходит 4 m .

Доказательство: Выделив в неизоморфных свободных деревьях по одной вершине, мы получаем неизоморфные ориентированные деревья. Упорядочивая поддеревья в неизоморфных ориентированных поддеревьях, мы получаем упорядоченные деревья. Поэтому число неизоморфных свободных деревьев с m ребрами не превосходит числа неизоморфных ориентированных деревьев с m дугами, которое в свою очередь не превосходит числа неизоморфных (различных) упорядоченных деревьев с m дугами. Отсюда из теоремы 3 следует утверждение следствия.

Бинарное дерево – это конечное множество вершин, которое либо пусто, либо состоит из корня и не более двух непересекающихся бинарных поддеревьев – левого и правого. Заметим, что бинарное дерево не является упорядоченным.

Пример: два различных бинарных дерева:

Эти деревья изоморфны как упорядоченные, ориентированные и свободные, но не изоморфны как бинарные деревья.

Источник

Ориентированные деревья. Упорядоченные деревья. Бинарные деревья.

Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.

Упорядоченное дерево — ордерево, в котором множество сыновей каждой вершины упорядочено; при изображении упорядоченного дерева предполагается, что указанные множества упорядочены слева направо.

Двои́чное де́рево — дерево, в котором каждый узел имеет не более двух потомков.

Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.

Плоский граф — геометрический граф, в котором никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины (не пересекаются). Является уложенным графом на плоскости.

Укладка: граф укладывается на некоторой поверхности, если его можно нарисовать на этой поверхности так, чтобы рёбра графа при этом не пересекались.

Эйлеров граф — граф, содержащий эйлеров цикл.

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Гамильтонов граф — граф, содержащий гамильтонову цепь или гамильтонов цикл.

Гамильтонов путь (или гамильтонова цепь) —путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом.

Простой конъюнкцией (дизъюнкцией) называется кон. (диз.) одной или нескольких переменных, при этом каждая переменная встречается не более одного раза( лидо сама, либо её отрицание).

Дизъюнктивной (конъюнктивной) нормальной формой ДНФ (КНФ) называется дизъюнкция (конъюнкция) простых конъюнкций (дизъюнкций).

Совершенной ДНФ (КНФ) называется такая ДНФ (КНФ), у которой в каждую конъюнкцию (дизъюнкцию) входят все переменные данного списка.

1. Представление логических функций в виде СДНФ (СКНФ).
2. Минимизация СДНФ (СКНФ).
3. Полные системы. Примеры полных систем (с доказательством полноты).
4. Теорема Жегалкина о представимости алгебры логики полиномом.

Любую функцию алгебры логики f(x₁, . ,x_n) можно единственным образом выразить полиномом Жегалкина над x₁, . ,x_n.

1. Понятие замкнутого класса. Замкнутость классов T₀, T₁ и L.
2. Двойственность. Класс самодвойственных функций, его замкнутость.
3. Класс монотонных функций, его замкнутость.
4. Лемма о несамодвойственной функции.
5. Лемма о немонотонной функции.
6. Лемма о нелинейной функции.
7. Теорема о полноте системы функций алгебры логики.
8. Теорема о максимальном числе функций в базисе алгебры логики.
9. Понятие схемы из функциональных элементов.
10. Проблема синтеза схем из функциональных элементов.
11. Элементарные методы синтеза.
12. Определение конечного автомата, способы задания автоматов.
13. Эквивалентность автоматов Мили и Мура.
14. Частичные автоматы. Постановка задачи минимизации автоматов.
15. Нахождение эквивалентных состояний.
16. Построение минимального автомата (случай всюду определенных условий).
17. Совместимые состояния частичных автоматов. Нахождение максимальной группировки.
18. Построение минимального частичного автомата.

Источник

Ориентированные, упорядоченные и бинарные деревья

Ориентированные (упорядоченные) деревья являются абстракцией иерархических отношений, которые очень часто встречаются как в практической жизни, так и в математике и в программировании. Дерево (ориентированное) и иерархия – это равнообъемные понятия.

Ориентированные деревья. Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами: 1)Существует единственный узел, полустепень захода которого равна 0. Он называется корнем ордерева.2)Полустепень захода всех остальных узлов равна 1.3)Каждый узел достижим из корня.

На рисунке приведены диаграммы всех различных ориентированных деревьев с 3 узлами, а на рисунке 2 показаны диаграммы всех различных ориентированных деревьев с 4 узлами.

__________

Теорема:Ордерево обладает следующими свойствами:1)Число рёбер равно числу вершин-1(свойство древовидности):q=p– 1.2)Если в ордереве отменить ориентацию ребер, то получится свободное дерево.3)В ордереве нет контуров.4)Для каждого узла существует единственный путь, ведущий в этот узел из корня.5)Подграф, определяемый множеством узлов, достижимых из узлаv, является ордеревом с корнем v (это ордерево называется поддеревом узла v).6)Если в свободном дереве любую вершину назначить корнем, то получится ордерево.

Замечание:Каждое свободное дерево определяет не более р ориентированных деревьев. Таким обра­зом, общее число различных ордеревьев с р узлами не более чем в р раз превосходит общее число различных свободных деревьев с р вершинами.

Концевая вершина ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева – это расстояние от корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.

Замечание:Наряду с «растительной» применяется еще и «генеалогическая» терминология. Узлы, достижимые из узла и, называются потомками узла и (потомки образуют поддерево). Если в дереве существует дуга (u,v), то узел0называется отцом (или родителем) узлаu, а узелvназывается сыном узлаu. Сыновья одного узла называются братьями.

Эквивалентное определение ордерева.

Ордерево T— это конечное множество узлов, таких что:1)Имеется один узелv, называемый корнем данного дерева;2)Остальные узлы (исключая корень) содержатся вkпопарно непересекающихся множествах.

Упорядоченные деревья.

Множества в эквивалентном определении ордерева являются поддеревьями.

Если относительный порядок поддеревьев фиксирован, то ордерево называется упорядоченным.

Представление в эвм свободных, ориентированных и упорядоченных деревьев.

Обсуждению представлений деревьев можно предпослать в точности те же рассуждения, что были предпосланы обсуждению представлений графов (см. раздел 7.4). Кроме того, следует подчеркнуть, что задача представления деревьев в программе встречается гораздо чаще, чем задача представления графов общего вида, а потому методы ее решения оказывают еще большее влияние на практику программирования.

Представление свободных, ориентированных и упорядоченных деревьев.

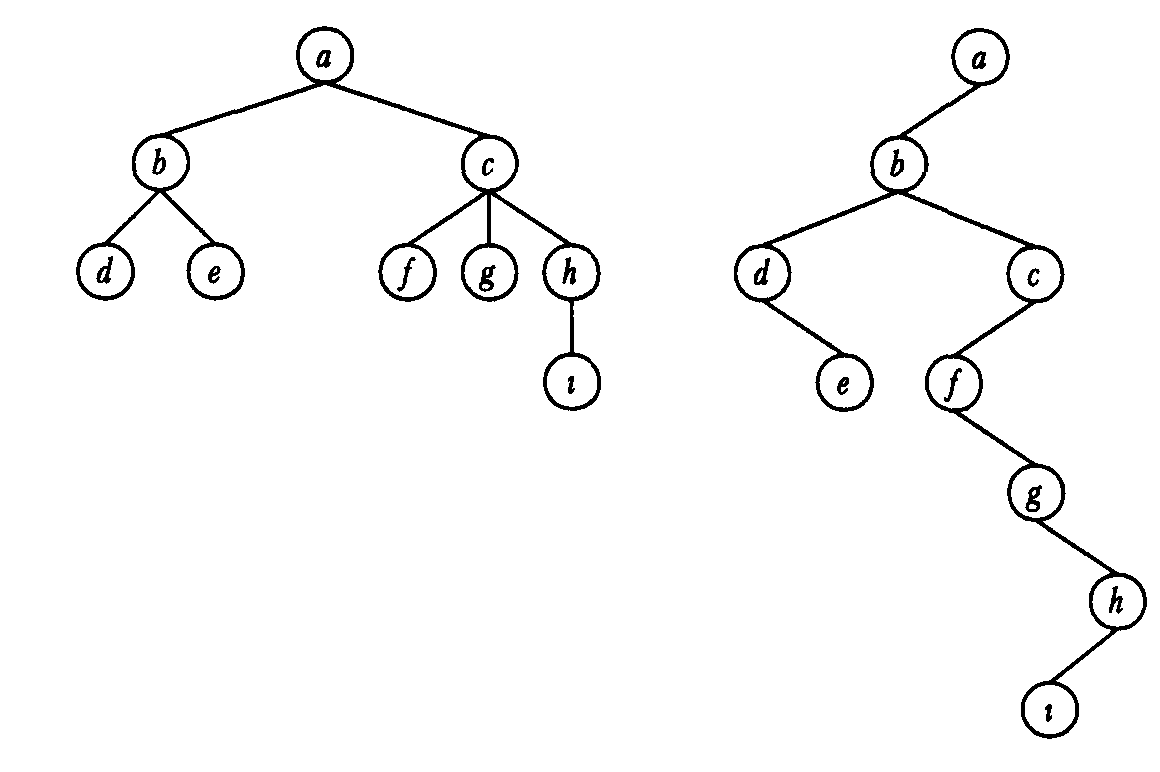
Всякое свободное дерево можно ориентировать, назначив один из узлов корнем. Всякое ордерево можно произвольно упорядочить. Всякое упорядоченное дерево можно представить бинарным деревом, проведя правую связь к старшему брату, а левую — к младшему сыну.

Замечание: Рассматривается генеологическая терминология. Узлы, достижимые из узла называются потомками. Если в дереве существует дугаu,v, то узелuназывают отцом, а узелv– сыном. Сыновья одного узла — братья

Пример:На рис. приведены диаграммы упорядоченного и соответствующего ему бинарного деревьев.

Таким образом, достаточно рассмотреть представление в ЭВМ бинарных деревьев.

Замечание:Из данного представления следует, что множество бинарных деревьев взаимнооднозначно соответствует множеству упорядоченных лесов упорядоченных деревьев.

Источник