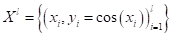31. Алгоритм cart построения дерева решений
алгоритм CART (Classification and Regression Tree – деревья классификации и регрессии). Деревья решений, построенные с помощью алгоритма CART, являются бинарными, то есть содержат только два потомка в каждом узле.
Пусть задано обучающее множество, содержащее примеров и классов. В алгоритме используется показатель эффективности разбиения, полученного на основе конкретного атрибута
где – показатель эффективности, – идентификатор разбиения, – идентификатор узла;
и – левый и правый потомки узла ;
– отношение числа примеров в левом потомке узла к общему числу примеров;
– отношение числа примеров в правом потомке узла к общему числу примеров;
– отношение числа примеров ‑ro класса в к общему числу примеров в ;
– отношение числа примеров ‑ro класса в к общему числу примеров в .
Тогда наилучшим разбиением в узле будет то, которое максимизирует показатель .
32. Принципы упрощения деревьев решений
Формально дерево решений будет строиться до тех пор, пока могут быть найдены новые разбиения, пока не будут получены абсолютно чистые листья или пока листья не будут содержать только одно наблюдение. В результате будет построено так называемое полное дерево. Полное дерево может быть сложным, те есть содержать много узлов и листьев. Полное дерево, как правило, является результатом переобучения (overfitting), то есть адаптации модели к частным случаям, нетипичным примерам, шумам в данных и т. п. Такое дерево идеально работает на обучающем множестве, но может давать много ошибок на тестовом множестве, на котором сеть не обучалась.
Другой крайностью является недообучение (underfitting). Недообученное дерево получается слишком простым, содержит мало разбиений и не обеспечивает высокую точность обучения.
Таким образом, необходимо найти баланс между точностью и сложностью дерева. Для этого используется комплекс методов, называемый упрощение дерева решений (pruning – отсечение, обрезка ветвей или reduction – сокращение, уменьшение).
Известны два основных подхода к выбору оптимальной сложности дерева решений [1]:
– ранняя остановка (preprunning);
– отсечение ветвей (postprunning).
Ранняя остановка означает, что при достижении некоторого условия рост дерева останавливается. В качестве условий остановки роста дерева принимают следующие:
– ошибка дерева: если отношение числа неправильно классифицированных записей к общему числу записей, поступивших в корневой узел, станет меньше заданной величины, то дальнейший рост дерева останавливается;
– минимальное допустимое количество примеров в узле: рост дерева останавливается, если количество примеров в узле станет меньше заданного;
– глубина дерева: задается допустимое число разбиений для каждой ветви;
– статистическая значимость разбиений: разбиение прекращается, если в результате разбиение примеров оказывается статистически незначимым, то то разбиение следует прекратить.
Идею отсечения ветвей рассмотрим на примере алгоритма CART [1, 15]. Для отсечения ветвей вводится понятие скорректированной ошибки дерева (поддерева)
где – показатель количества ошибок (в простейшем случае это количество ошибок классификации, допущенных деревом в данном узле); – число листов (терминальных узлов) дерева, – некоторый параметр, который постепенно увеличивается по мере создания новых поддеревьев.
Скорректированная ошибка дерева состоит из двух компонент – ошибки классификации дерева и штрафа за его сложность. Тогда менее ветвистое дерево, дающее большую ошибку классификации, будет иметь меньшую скорректированную ошибку, чем дерево, дающее меньшую ошибку, но более ветвистое.
Сначала строится полное дерево, а затем производится его упрощение путем отсечения ветвей. Для этого находятся все поддеревья‑кандидаты. Первым кандидатом является полное дерево. Остальные поддеревья получаются отсечение листьев (все кандидаты содержат корневой узел). Для каждого кандидата вычисляется скорректированная ошибка. Если скорректированная ошибка поддерева меньше скорректированной ошибки полного дерева, то данное поддерево является кандидатом на модель.
Когда определены все поддеревья‑кандидаты, из них выбирается лучшее, дающее наименьшую ошибку на тестовых данных, на которых дерево не обучалось. Рассмотренную процедуру можно применить к выбранному поддереву т. д., пока ошибка не превысит допустимую величину.
Ранняя остановка проще отсечения ветвей, но возникает риск потери хороших разбиений, которые могут следовать за плохими. Поэтому отсечение ветвей, как правило, дает лучшие результаты и шире используется
Источник
Решающие деревья в задачах регрессии. Алгоритм CART
На предыдущих занятиях мы с вами рассматривали решающие деревья для задач классификации. Однако, в ряде случаев, их применяют и для задач регрессии, когда алгоритм на выходе формирует одно вещественное значение (или несколько значений) для каждого входного вектора . То есть, в листьях такого дерева хранятся соответствующие вещественные числа.
Давайте, для определенности, я сразу приведу пример такого решающего дерева.
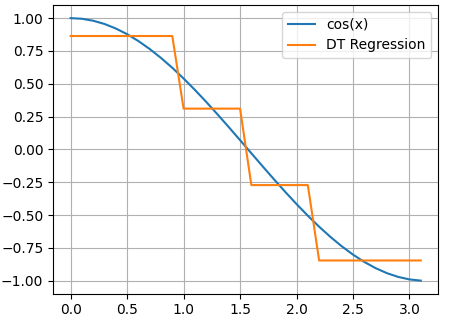
Смотрите, изначально наши данные представляют собой точки функции cos(x):
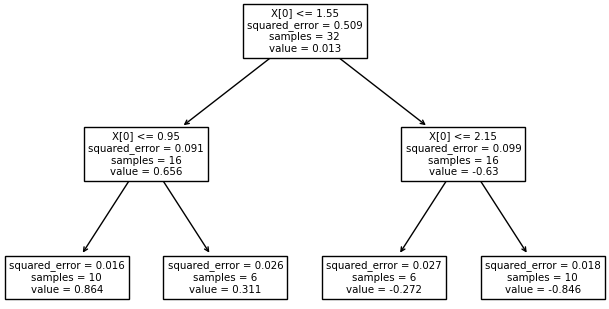
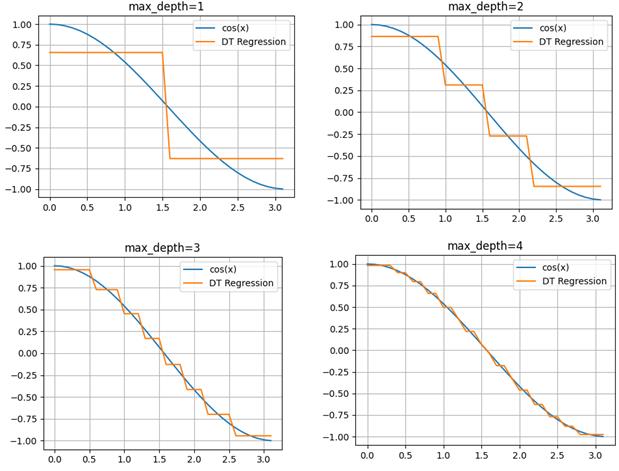
Здесь аргумент функции cos() – это признак, а значения функции в каждой точке – целевые переменные. Затем, по признаку (аргументу функции) выполняется разделение исходного множества точек на непересекающиеся подмножества. В результате, при глубине дерева два, получаем четыре подинтервала и четыре листа. Причем, в каждом листе хранится одно константное вещественное значение, которым заменяются все значения выделенного подмножества. Поэтому мы видим на графике ступенчатую функцию при аппроксимации косинусоиды решающим деревом.
Вот общая идея использования решающих деревьев для задач регрессии. И здесь возникают два главных вопроса:
- По какому критерию оценивать качество деления на подмножества (то есть, что использовать в качестве меры неопределенности – impurity)?
- Как вычислять вещественные значения в полученных листовых вершинах?
Хорошая новость, что на оба этих вопроса имеется единый ответ. Я начну с последнего. Часто в задачах регрессии требуется обеспечить минимум среднеквадратичной ошибки прогноза: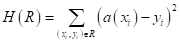 
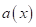
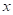
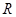
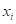
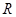
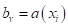
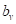
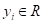
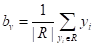
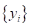
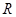
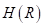
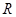
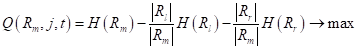
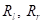
Здесь 
— ответ (прогноз) модели на входной вектор признаков ; 
— множество объектов 
, дошедших до некоторой листовой вершины v, и соответствующие им целевые значения 
. Так как при использовании решающих деревьев каждое подмножество аппроксимируется некоторым константным значением: 
то для минимизации квадратичного критерия, величину 
следует вычислять, как среднее арифметическое от всех целевых значений 
, попавших в листовую вершину v дерева: 
Можно легко доказать, что эта величина будет наилучшим образом описывать значения подмножества при квадратичном критерии. Так как величина 
зависит от множества , а значит, от способа разбиения деревом исходной обучающей выборки, то ее было бы логично использовать в качестве меры информативности (impurity) и выбирать в каждой промежуточной вершине разбиение так, чтобы максимизировался информационный выигрыш: 
То есть, мы будем выбирать порог t так, чтобы impurity левого и правого подмножеств 
были как можно меньше. Вот примеры разбиения исходной последовательности деревом глубиной от единицы до четырех: 
Как видите, вначале выделяются два равных подмножества и две константы, которые грубо описывают график косинусоиды. И это описание наилучшее с точки зрения квадратического критерия. При увеличении глубины, получаем все больше и больше информации об исходном сигнале, и для глубины 4 вполне угадывается график косинусоиды.
Реализация решающих деревьев на Python с помощью Scikit-Learn
Итак, мы с вами в целом познакомились с идеей решающих деревьев для задач классификации и регрессии. Осталось узнать, как можно реализовать эти подходы при решении практических задач. В самом простом варианте это можно сделать на языке Python с использованием библиотеки Scikit-Learn. В этой библиотеке имеется ветка:
которая отвечает за построение решающих деревьев. Разработчики Scikit-Learn использовали алгоритм: Classification and Regression Trees (CART) с помощью которого можно выполнять как классификацию, так и решать задачи регрессии. Подробнее об этом можно почитать на странице официальной документации: https://scikit-learn.org/stable/modules/tree.html Давайте, вначале построим решающее дерево для задачи регрессии. Для этого сформируем обучающее множество в виде значений функции косинуса:
import numpy as np import matplotlib.pyplot as plt x = np.arange(0, np.pi, 0.1).reshape(-1, 1) y = np.cos(x)
clf = tree.DecisionTreeRegressor(max_depth=3) clf = clf.fit(x, y)
Источник
Алгоритм CART (CART algorithm)
Популярный алгоритм построения деревьев решений, который может работать как с дискретной, так и с непрерывной выходной переменной, т.е. решать задачи и классификации, и регрессии.
Алгоритм строит бинарные деревья решений, которые содержат только два потомка в каждом узле. В процессе работы происходит рекурсивное разбиение примеров обучающего множества на подмножества, записи в которых имеют одинаковые значения целевой переменной.
Алгоритм реализует обучение с учителем и использует в качестве критерия для выбора разбиений в узлах индекс чистоты Джини (Gini impurity index). В процессе роста дерева алгоритм CART проводит для каждого узла полный перебор всех атрибутов, на основе которых может быть построено разбиение, и выбирает тот, который максимизирует значение индекса Джини.
Основная идея алгоритма заключается в том, чтобы выбрать такое разбиение из всех возможных в данном узле, чтобы полученные дочерние узлы были максимально однородными. При этом каждое разбиение производится только по одному атрибуту.
Если атрибут X , по которому производится разбиение, является номинальным c I категориями, то для него существует 2 ( I − 1 ) возможных разбиения, а если порядковым или непрерывным с K различными значениями, существует K − 1 различных разбиений по X . Дерево строится, начиная с корневого узла, путем итеративного использования следующих шагов в каждом узле:
- Для каждого атрибута ищется лучшее разбиение (в смысле однородности результирующих подмножеств).
- Среди всех разбиений, найденных на предыдущем шаге, выбирается то, для которого критерий разбиения наибольший.
- Узел разбивается с использованием лучшего разбиения, найденного на шаге 2, если не выполнено условие остановки.
Процедура упрощения деревьев решений, построенных на основе алгоритма CART, реализуется с помощью специального метода соотношения издержки-сложность (Cost-Complexity Pruning) и перекрестной проверки (для малых наборов данных, где полноценное разделение на обучающее и тестовое множества проблематично).
Алгоритм обладает следующими преимуществами:
- не является статистическим, поэтому не требует вычисления параметров вероятностных распределений;
- атрибуты разбиения выбираются непосредственно в процессе построения дерева, поэтому нет необходимости проводить процедуру отбора переменных для модели;
- устойчив к выбросам и аномальным значениям;
- высокая скорость работы.
К недостаткам алгоритма можно отнести неустойчивость относительно данных: даже небольшие изменения в обучающем множестве порождают значительные изменения в структуре дерева решений.
Алгоритм предложен в 1984 г. Лео Брейманом, Джеромом Фридманом, Ричардом Олшеном и Чарльзом Стоуном.
Источник