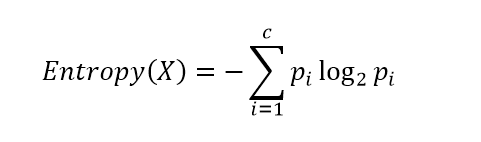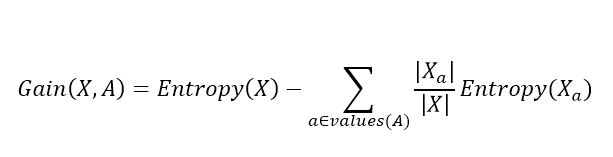Использование деревьев решений в задачах прогнозной аналитики
В последние десятилетия одними из самых популярных методов решения задач прогнозной аналитики являются методы построения деревьев решений. Эти методы универсальны, используют эффективную процедуру вычислений, позволяют найти достаточно качественное решение задачи. Именно об этих методах я расскажу в данной статье.
Дерево решений
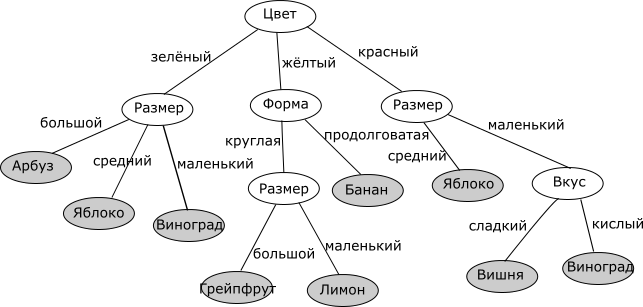
Дерево решений – структура данных, в процессе обхода которой в каждом узле в зависимости от проверяемого условия принимается определенное решение – перемещение по той или иной ветке дерева от корня к «листьевым» (конечным) вершинам. В «листьевой» вершине дерева содержится искомое значение интересующего атрибута. Деревья решений могут оценивать значения категориальных атрибутов (конечное число дискретных значений), а также количественных. В первом случае говорят о задаче классификации – отнесении объекта к одному из «классов», определяемых атрибутом (например, Да/Нет, Хорошо/Удовлетворительно/Плохо и т.д.). Во втором случае говорят о задаче регрессии, то есть об оценке количественной величины.
Мы рассмотрим алгоритм, позволяющий построить такое дерево решений для оценивания и предсказания значений интересующего нас категориального атрибута анализируемого набора данных на основе значений других атрибутов (задача классификации).
Вообще способов построить дерево может быть бесконечно много – атрибуты можно рассматривать в разном порядке, проверять в узлах дерева различные условия, останавливать процесс, используя разные критерии. Но нас интересуют только деревья, которые наиболее точно оценивают значение атрибута, с минимальной ошибкой, а также позволяют выявлять зависимость между атрибутами и успешно выполнять прогнозирование значений атрибутов на новых данных. К сожалению, не существует хороших алгоритмов, позволяющих гарантированно найти такое «оптимальное» дерево (за приемлемое время). Однако существуют достаточно хорошие алгоритмы, которые пытаются построить «почти оптимальное» дерево, выполняя на каждой итерации определенный «локальный» критерий оптимальности в надежде, что получившееся дерево тоже в целом будет «оптимальным». Такие алгоритмы называются «жадными». Именно такой алгоритм мы и рассмотрим.
Алгоритм построения дерева решений
Принцип построения дерева следующий. Дерево строится «сверху вниз» от корня. Начинается процесс с определения, какой атрибут следует выбрать для проверки в корне дерева. Для этого каждый атрибут исследуется на предмет, как хорошо он в одиночку классифицирует набор данных (разделяет на классы по целевому атрибуту). Когда атрибут выбран, для каждого его значения создается ветка дерева, набор данных разделяется в соответствии со значением к каждой ветке, процесс повторяется рекурсивно для каждой ветки. Также следует проверять критерий остановки.
Главный вопрос – как выбирать атрибуты. В соответствии с идеей подхода, когда в концевых узлах дерева (листьях) будет искомый нами класс целевого атрибута, необходимо, чтобы при разбиении набора данных в каждом узле получавшиеся наборы данных были все более однородны в плане значений классов (например, большинство объектов в наборе принадлежало бы к классу Арбуз). И необходимо определить количественный критерий, чтобы оценить однородность разбиения.
Энтропия
Рассмотрим набор вероятностей pi, описывающий вероятность соответствия строки данных в нашем наборе (обозначим его X) классу i. Вычислим следующую величину:
Данная функция представляет собой так называемую энтропию. Энтропия возникла в теории информации и описывает количество информации (в битах), которое необходимо, чтобы закодировать сообщение о принадлежности случайно выбранного объекта (строки) из нашего набора X к одному из классов и передать его получателю. Если класс только один, получателю ничего не нужно передавать, энтропия равна 0 (принимается, что 0log20 = 0). Если все классы равновероятны, то потребуется log2c бит (c – общее количество классов) – максимум функции энтропии.
Далее, для выбора атрибута, для каждого атрибута A вычисляется так называемый прирост информации:
Где values(A) – все принимаемые значения атрибута A, Xa – подмножество набора данных, где A = a, |X| – количество элементов во множестве. Данная величина описывает ожидаемое уменьшение энтропии после разбиения набора данных по выбранному атрибуту. Второе слагаемое – это сумма энтропий для каждого подмножества, взятая со своим весом. Общая разница описывает, как уменьшится энтропия, сколько мы сэкономим бит для кодирования класса случайного объекта из набора X, если мы знаем значения атрибута A и разобьем набор данных на подмножества по данному атрибуту.
Алгоритм выбирает атрибут, соответствующий максимальному значению прироста информации.
Когда атрибут выбран, исходный набор разбивается на подмножества в соответствии с его значениями, исходный атрибут исключается из анализа, процесс повторяется рекурсивно.
Процесс останавливается, когда созданные подмножества стали достаточно однородны (преобладает один класс), а именно когда max(Gain(X,A)) становится меньше некоторого заданного параметра Θ (величина, близкая к 0). Как альтернативный вариант, можно контролировать само множество X, и когда оно стало достаточно мало или стало полностью однородным (только один класс), останавливать процесс.
Жадный алгоритм построения дерева решений
Более структурно алгоритм можно представить следующим образом:
1. Если max(Gain(X,A))
Источник
Классификация и регрессия с помощью деревьев принятия решений
В данной статье сделан обзор деревьев принятия решений (Decision trees) и трех основных алгоритмов, использующих эти деревья для построение классификационных и регрессионных моделей. В свою очередь будет показано, как деревья принятия решения, изначально ориентированные на классификацию, используются для регрессии.
Деревья принятия решений
Дерево принятия решений — это дерево, в листьях которого стоят значения целевой функции, а в остальных узлах — условия перехода (к примеру “ПОЛ есть МУЖСКОЙ”), определяющие по какому из ребер идти. Если для данного наблюдения условие истина то осуществляется переход по левому ребру, если же ложь — по правому.
Классификация
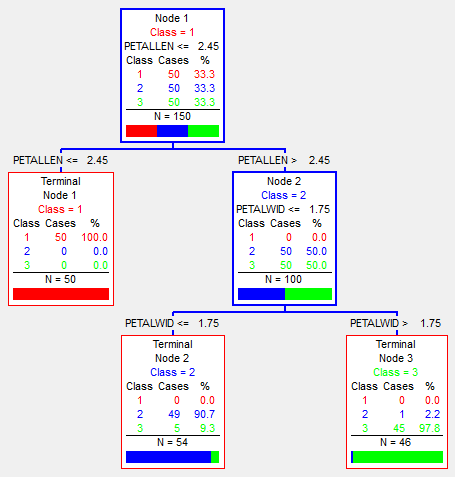
На изображении приведенном выше показано дерево классификации ирисов. Классификация идет на три класса (на изображении помечены — красным, синим и зеленым), и проходит по параметрам: длина\толщина чашелистика (SepalLen, SepalWid) и длина\толщина лепестка (PetalLen, PetalWid). Как видим, в каждом узле стоит его принадлежность к классу (в зависимости от того, каких элементов больше попало в этот узел), количество попавших туда наблюдений N, а так же количество каждого класса. Так же не в листовых вершинах есть условие перехода — в одну из дочерних. Соответственно, по этим условиям и разбивается выборка. В результате, это дерево почти идеально (6 из 150 неправильно) классифицировало исходные данные (именно исходные — те на которых оно обучалось).
Регрессия
Если при классификации в листах стоят результирующие классы, при регрессии же стоит какое-то значение целевой функции.
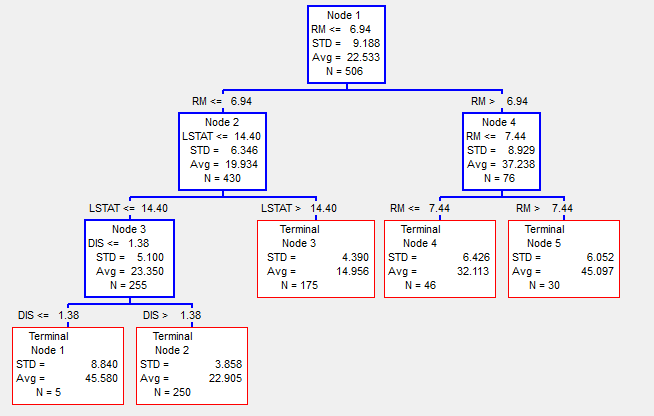
На выше приведенном изображении регрессионное дерево, для определения цены на землю в городе Бостон в 1978 году, в зависимости от параметров RM — количество комнат, LSTAT — процент неимущих и нескольких других параметров (более детально можно посмотреть в [4]). Соответственно, здесь в каждом узле мы видим среднее значение (Avg) и стандартное отклонение (STD) значений целевой функции наблюдений попавших в эту вершину. Общее количество наблюдений попавших в узел N. Результатом регрессии будет то значение среднего (Avg), в какой узел попадёт наблюдение.
Таким образом изначально классификационное дерево, может работать и для регрессии. Однако при таком подходе, обычно требуются большие размеры дерева, чем при классификации, что бы достигнуть хороших результатов регрессии.
Основные методы
Ниже перечислены несколько основных методов, которые используют деревья принятия решений. Их краткое описание, плюсы и минусы.
CART
CART (англ. Classification and regression trees — Классификационные и регрессионные деревья) был первым из методов, придуманный в 1983 четверкой известных ученых в области анализа данных: Leo Breiman, Jerome Friedman, Richard Olshen and Stone [1].
Суть этого алгоритма состоит в обычном построении дерева принятия решений, не больше и не меньше.
На первой итерации мы строим все возможные (в дискретном смысле) гиперплоскости, которые разбивали бы наше пространство на два. Для каждого такого разбиения пространства считается количество наблюдений в каждом из подпространств разных классов. В результате выбирается такое разбиение, которое максимально выделило в одном из подпространств наблюдения одного из классов. Соответственно, это разбиение будет нашим корнем дерева принятия решений, а листами на данной итерации будет два разбиения.
На следующих итерациях мы берем один худший (в смысле отношения количества наблюдений разных классов) лист и проводим ту же операцию по разбиению его. В результате этот лист становится узлом с каким-то разбиением, и двумя листами.
Продолжаем так делать, пока не достигнем ограничения по количеству узлов, либо от одной итерации к другой перестанет улучшаться общая ошибка (количество неправильно классифицированных наблюдений всем деревом). Однако, полученное дерево будет “переобучено” (будет подогнано под обучающую выборку) и, соответственно, не будет давать нормальные результаты на других данных. Для того, что бы избежать “переобучения”, используют тестовые выборки (либо кросс-валидацию) и, соответственно, проводится обратный анализ (так называемый pruning), когда дерево уменьшают в зависимости от результата на тестовой выборке.
Относительно простой алгоритм, в результате которого получается одно дерево принятия решений. За счет этого, он удобен для первичного анализа данных, к примеру, что бы проверить на наличие связей между переменными и другим.



RandomForest
Random forest (Случайный лес) — метод, придуманный после CART одним из четверки — Leo Breiman в соавторстве с Adele Cutler [2], в основе которого лежит использование комитета (ансамбля) деревьев принятия решений.
Суть алгоритма, что на каждой итерации делается случайная выборка переменных, после чего, на этой новой выборке запускают построение дерева принятия решений. При этом производится “bagging” — выборка случайных двух третей наблюдений для обучения, а оставшаяся треть используется для оценки результата. Такую операцию проделывают сотни или тысячи раз. Результирующая модель будет будет результатом “голосования” набора полученных при моделировании деревьев.






Stochastic Gradient Boosting
Stochastic Gradient Boosting (Стохастическое градиентное добавление) — метод анализа данных, представленный Jerome Friedman [3] в 1999 году, и представляющий собой решение задачи регрессии (к которой можно свести классификацию) методом построения комитета (ансамбля) “слабых” предсказывающих деревьев принятия решений.
На первой итерации строится ограниченное по количеству узлов дерево принятия решений. После чего считается разность между тем, что предсказало полученное дерево умноженное на learnrate (коэффициент “слабости” каждого дерева) и искомой переменной на этом шаге.
Yi+1=Yi-Yi*learnrate
И уже по этой разнице строится следующая итерация. Так продолжается, пока результат не перестанет улучшаться. Т.е. на каждом шаге мы пытаемся исправить ошибки предыдущего дерева. Однако здесь лучше использовать проверочные данные (не участвовавшие в моделировании), так как на обучающих данных возможно переобучение.







Заключение
Список литературы
- “Classification and Regression Trees”. Breiman L., Friedman J. H., Olshen R. A, Stone C. J.
- “Random Forests”. Breiman L.
- “Stochastic Gradient Boosting”. Friedman J. H.
- http://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
Источник