Деревья решений при оценке кредитоспособности
Панягина Ася Евгеньевна
Муромский институт (филиал) Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых
кандидат экономических наук, доцент кафедры экономики
Аннотация
В статье обосновывается целесообразность применения метода дерева решений для оценки кредитного риска. В отличие от широко распространенных скоринговых моделей, этот метод позволяет не только оценить вероятность реализации рискового события, но и учесть размер потенциально возможного дохода и его изменчивость.
Panyagina Asya Evgenyevna
Murom Institute (branch) of Vladimir State University name after Aleksandr Grigorevich and Nikolay Grigorevich Stoletovs
PhD, Associate Professor of Economics
Abstract
The article substantiates the feasibility of the application of the method of decision tree for estimation of credit risk. In contrast to the widespread scoring models, this method allows not only to estimate the likelihood of a risk event, but also to consider the size of the potential income and its variability.
Библиографическая ссылка на статью:
Панягина А.Е. Использование метода «дерево решений» для оценки кредитного риска // Экономика и менеджмент инновационных технологий. 2013. № 9 [Электронный ресурс]. URL: https://ekonomika.snauka.ru/2013/09/2978 (дата обращения: 14.08.2023).
В современной практике банковского кредитования для оценки кредитного риска широко применяется скоринговые модели, в частности, их используют «Русский стандарт», «Райффайзенбанк», «Ситибанк», «ЮниКредит банк». В разных сегментах рынка кредитных ресурсов доля банков, применяющих или собирающихся в ближайшем будущем применять скоринговую оценку, составляет от 20% до 83% [1, с. 52-53]. На российском рынке представлены специализированные компании, разрабатывающие методики скорингового анализа и предлагающие соответствующее программное обеспечение: Credit Scoring Solution, EGAR Application Scoring, SAS Institute. Не снижается актуальность научных исследований, направленных на выявление преимуществ и недостатков и совершенствование скоринговой оценки [1, 2, 3, 4].
Столь активное внедрение скоринга в практику оценки кредитного риска обусловлено целым рядом обеспечиваемых с его помощью преимуществ – скоростью, низкими издержками, исключением субъективизма оценки, возможностью отсечь до 90% ненадежных заемщиков и улучшением качества кредитного портфеля в целом. По мнению автора, наиболее весомым аргументом в пользу скоринговых моделей следует признать возможность определения вероятности неблагоприятного исхода (невозврата кредита) с приемлемой точностью. Но при этом не следует забывать о двойственной природе категории риска, возможности получения не только отрицательного и нулевого, но и положительного результата. Измерение риска не заканчивается установлением вероятности реализации рискового события – не меньшее значение имеет размер потенциально возможного дохода и его изменчивость. Метод «дерева решений» позволяет учесть эти характеристики при принятии решения о кредитовании и, по мнению автора, повышает обоснованность такого решения.
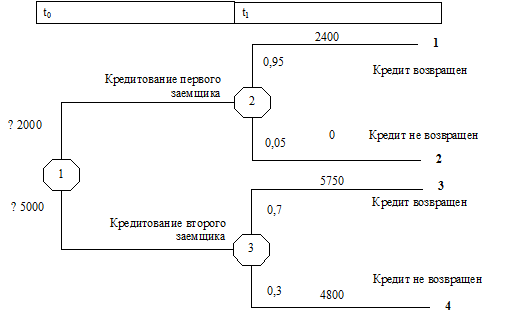
Рассмотрим конкретную ситуацию. Банк осуществляет выбор между двумя вариантами кредитования. В первом варианте запрашивается кредит в сумме 2000 тыс. руб., сроком на 1 год, ставка процента может быть установлена в размере 20% годовых. Вероятность возврата кредита, оцененная банком с использованием скоринговой модели, составляет 0,95. Обеспечение отсутствует.
По второму варианту кредитования запрашивается кредит в сумме 5000 тыс. руб., сроком на 1 год, ставка процента может быть установлена в размере 15% годовых. Вероятность возврата 0,7. Предоставляется обеспечение в форме залога, рыночная стоимость которого с учетом затрат на востребование и реализацию при невозврате заемных средств составляет 4800 тыс. руб.
При построении дерева может быть выделено два этапа – этап принятия решения о кредитовании (момент времени t0) и этап возврата средств (момент времени t1).
1 этап. В момент времени t0 (событие 1) может быть принято решение о кредитовании первого либо второго заемщика. На этом этапе отток средств составляет 2000 тыс. руб. при первом варианте кредитования и 5000 тыс. руб. при втором.
2 этап. В момент времени t1 возможны четыре варианта развития событий (четыре ветви дерева):
1 – кредит и проценты по нему будет погашены первым заемщиком в сумме 2400 тыс. руб. (2000 тыс. руб. – основной долг, 400 тыс. руб. – сумма процентов) с вероятностью 0,95;
2 – кредит и проценты не будут погашены с вероятностью 0,05, при этом прямые потери банка составят 2000 тыс. руб.
3 – кредит и проценты по нему будет погашены вторым заемщиком в сумме 5750 тыс. руб. (5000 тыс. руб. – основной долг, 750 тыс. руб. – сумма процентов) с вероятностью 0,7;
4 – кредит и проценты не будут погашены с вероятностью 0,3, при этом прямые потери банка составят, с учетом взыскания залога 200 тыс. руб. (5000 тыс. руб. – 4800 руб.)
Дерево решений, построенное для данной финансово-хозяйственной ситуации, показано на рис. 4. Критерием для принятия решения о кредитовании могут служить статистические показатели оценки степени риска, расчет которых показан в таблице 1.
Рисунок 4 – Дерево решений для оценки кредитного риска
Таблица 1 – Оценка кредитного риска по методу «Дерево решений»
Источник
Дерево решений
Для построения дерева решений не существует универсального набора символов, но чаще всего квадраты (□) используются для представления «решений», а круги (○) для представления «результатов». Поэтому я буду использовать в своей статье именно эти символы.
Дерево решений и задача, требующая многошагового принятия решений
Дерево решений – это представление задачи в виде диаграммы, отражающей варианты действий, которые могут быть предприняты в каждой конкретной ситуации, а также возможные исходы (результаты) каждого действия. Такой подход особенно полезен, когда необходимо принять ряд последовательных решений и (или) когда на каждом этапе процесса принятия решения могут возникать множественные исходы.
Например, если рассматривается вопрос, стоит ли расширять бизнес, решение может зависеть более чем от одной переменной.
Например, может существовать неопределенность как в отношении объема продаж, так и величины затрат. Более того, значение некоторых переменных может зависеть от значения других переменных: например, если будет продано 100,000 единиц продукта, себестоимость единицы продукта составит $4, но если будет продано 120,000 единиц, себестоимость единицы снизится до $3.80. Таким образом, возможны различные исходы ситуации, при этом некоторые из них будут зависеть от предыдущих исходов. Дерево решений представляет собой полезный метод разделения сложной задачи на более мелкие и более управляемые подзадачи.
Решение задачи при помощи дерева решений осуществляется в два этапа. Первый этап включает построение дерева решений с указанием всех возможных исходов (финансовых результатов) и их вероятностей. Следует помнить, что при принятии решений нужно опираться на принцип релевантных затрат, т. е. использовать только релевантные затраты и выручку. Второй этап включает оценку и формулировку рекомендаций. Принятие решения осуществляется путем последовательного расчета ожидаемых значений исходов в обратном порядке от конца к началу (справа налево). После этого формируются рекомендации для руководства по выбору оптимального образа действий.
Построение дерева решений
Дерево решений всегда следует строить слева направо. Выше я упоминал «решения» и «исходы». Точки принятия решений представляют собой варианты альтернативных действий, то есть возможные выборы. Вы принимаете решение пойти либо этим, либо другим путем. Исходы (результаты решений) от вас не зависят. Они зависят от внешней среды, например, от клиентов, поставщиков или состояния экономики в целом. Как из точек принятия решений, так и из точек исходов выходят «ветви» дерева. Если существует, например, два возможный варианта действий, из точки принятия решения будут выходить две ветви, и если существует два возможных исхода (например, хороший и плохой), то из точки исхода тоже будут выходить две ветви. Поскольку дерево решений является инструментом оценки различных вариантов действий, то все деревья решений должны начинаться с точки принятия решения, которая графически представляется квадратом.
Пример простого дерева решений показан ниже. Из рисунка видно, что лицо, принимающее решение, может выбрать из двух вариантов, поскольку из точки
принятия решения выходит две ветви. Исход одного из вариантов действий, представленного верхней ветвью, точно известен, поскольку на этой ветви нет никаких точек возможных исходов. Но на нижней ветви есть круг, который показывает, что в результате данного решения возможны два исхода, поэтому из него исходят две ветви. На каждой из этих двух ветвей тоже имеется по кругу, из которых, в свою очередь, тоже выходят по две ветви. Это значит, что для каждого из упомянутых возможных исходов имеется два варианта развития ситуации, и каждый из вариантов имеет свой исход. Возможно, первые два исхода представляют собой различные уровни дохода в случае осуществления определенной инвестиции, а второй ряд исходов — различные варианты переменных затрат для каждого уровня доходов.
После построения основы дерева, как показано выше, необходимо указать финансовые значения исходов и их вероятности. Важно помнить, что вероятности, указанные для ветвей, исходящих из одной точки, в сумме должны давать 100%, иначе это будет означать, что вы не указали на диаграмме какой-либо результат, или допустили ошибку в расчетах. Пример приведен ниже в статье.
После построение дерева решений необходимо оценить решение.
Оценка решения
Дерево решений оценивается справа налево, т. е. в направлении, обратном тому, которое использовалось для построения дерева решений. Для того, чтобы осуществить оценку, вы должны предпринять следующие шаги:
- Подпишите все точки принятия решений и исходов, т.е. все квадраты и круги. Начните с тех, которые расположены в самой правой части диаграммы, сверху вниз, и затем перемещайтесь влево до самого левого края диаграммы.
- Последовательно рассчитайте ожидаемые значения всех исходов, двигаясь справа налево, используя финансовые показатели исходов и их вероятности.
Наконец, выберите вариант, который обеспечивает максимальное ожидаемое значение исхода и подготовьте рекомендации для руководства.
Важно помнить, что использование ожидаемых значений для принятия решения имеет свои недостатки. Ожидаемое значение – это средневзвешенное значение исходов решения в долгосрочной перспективе, если бы это решение принималось много раз.
Таким образом, если мы принимаем однократное решение, то фактический результат
быть далек от ожидаемого значения, поэтому данный метод нельзя назвать очень точным. Кроме того, рассчитать точные вероятности довольно сложно, поскольку конкретная рассматриваемая ситуация могла никогда не случаться в прошлом.
Метод ожидаемого значения при принятии решений полезен тогда, когда инвестор имеет нейтральное отношение к риску. Такой инвестор не принимает на себя чрезмерные риски, но и не избегает их. Если отношение к риску лица, принимающего решение, неизвестно, то сложно сказать, стоит ли использовать метод ожидаемого значения. Может оказаться более полезным просто рассмотреть наихудший и наилучший сценарии, чтобы создать основу для принятия решения.
Я приведу простой пример использования дерева решений. В целях упрощения считайте, что все цифры являются чистой приведенной стоимостью соответствующего показателя.
Пример 1
Компания принимает решение, стоит ли разрабатывать и запускать новый продукт. Ожидается, что затраты на разработку составят $400,000, при этом вероятность того, продукт окажется успешным, составляет 70%, а вероятность неудачи, соответственно, 30%. Ниже приведена оценка прибыли от продажи продукта, в зависимости от уровня спроса – высокого, среднего или низкого, а также соответствующие каждому уровню вероятности:
Источник