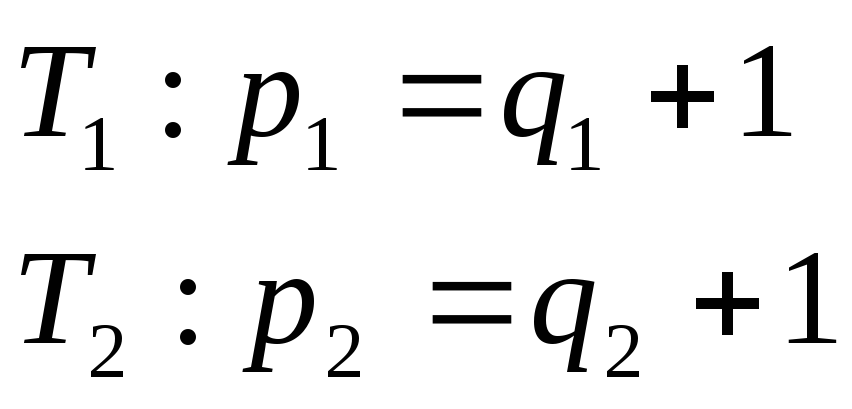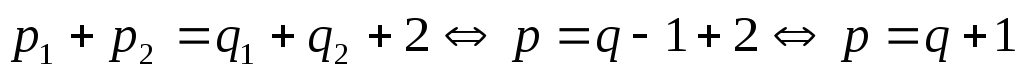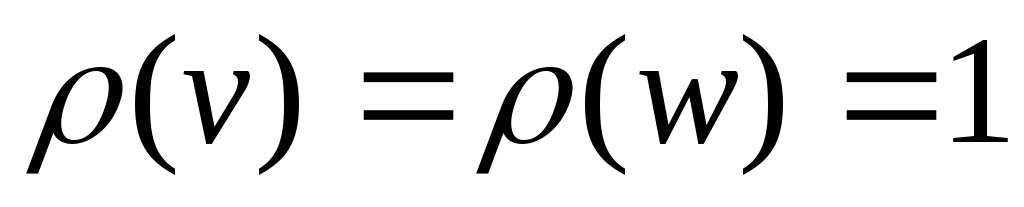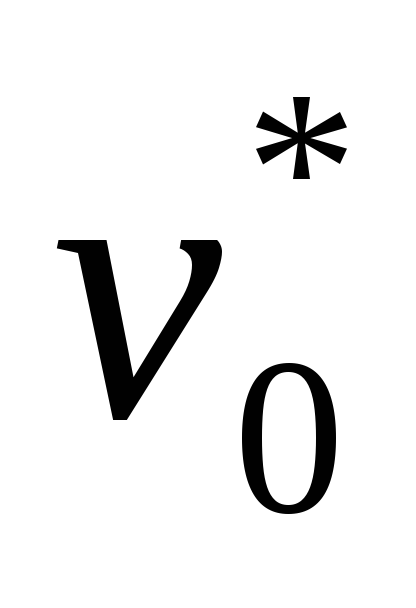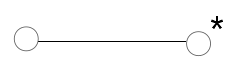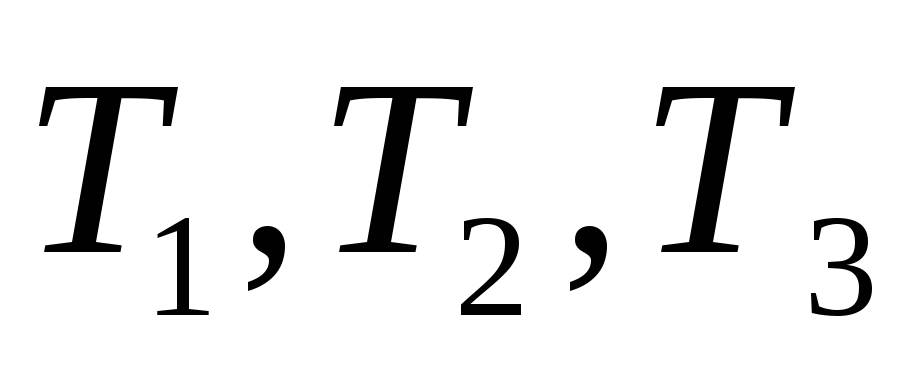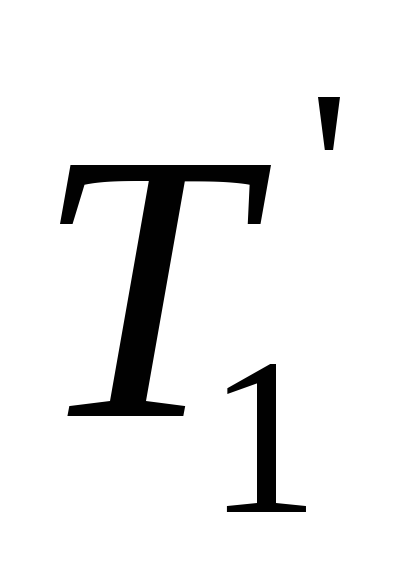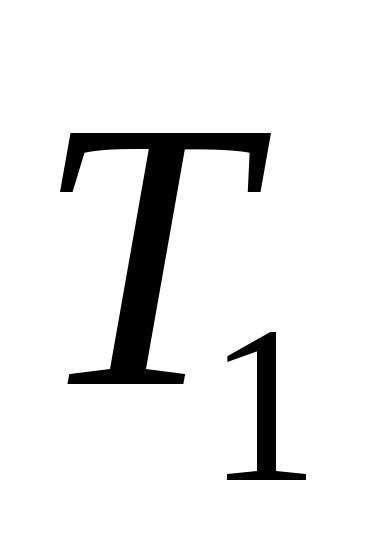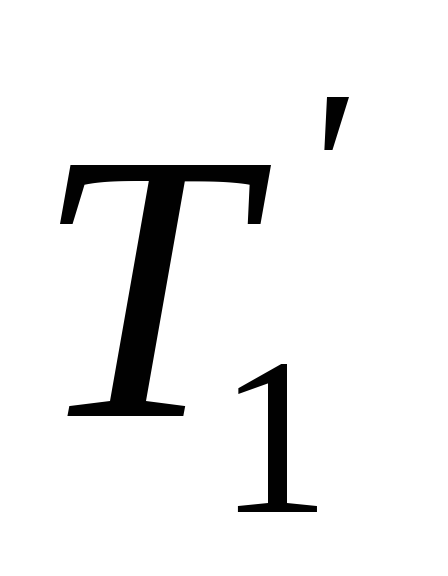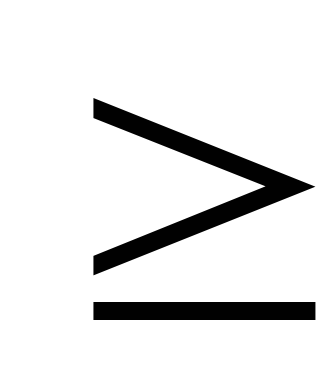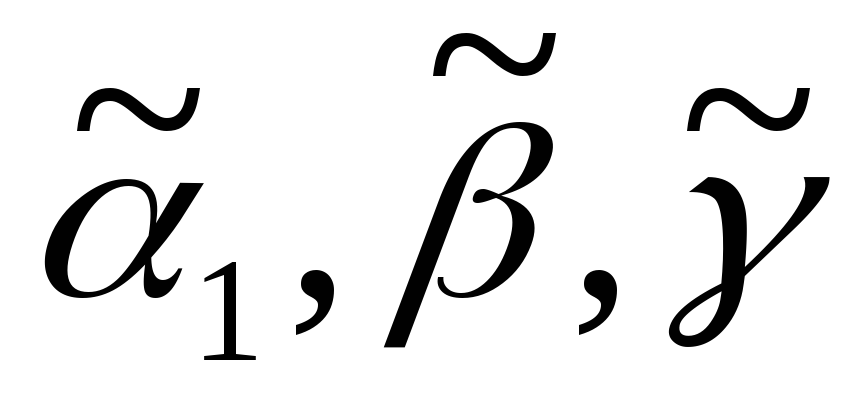Деревья свойства деревьев примеры

20-ка Полезных свойств деревьев

Деревья — это наши лучшие друзья . Если Вы сомневаетесь в этом, тогда представляем вашему вниманию 20 главных причин, из-за которых стоит сажать, ухаживать и защищать деревья.

#1: Борются с парниковым эффектом

Глобальное потепление стало результатом избытка парниковых газов, созданных при горении ископаемого топлива и истребления тропического леса. Солнечное тепло, отражаясь от Земли, попадает в ловушку из слоя парниковых газов, в результате чего, уровень мировой температуры постоянно растет. Углекислый газ (CO2) считается одним из главных парниковых газов. Деревья, в процессе фотосинтеза, перерабатывают СО2 на кислород. В течение одного года, акр взрослых деревьев поглощает количество CO2, которое вырабатывает автомобиль проехавший 26000 миль.

#2: Очищают воздух

Деревья поглощают запахи и газы загрязняющих веществ (оксиды азота, аммиак, диоксид серы и озон), а также фильтруют твердые частицы из воздуха, путем захвата их на листья и кору.

#3: Обеспечивают нас кислородом

За один год, акр зрелых деревьев, может обеспечить кислородом 18 человек.

#4: Остужают улицы и города

В течение последних 50 лет из-за масштабного строительства и снижения количества зеленых насаждений средняя температура в городах заметно увеличилась. Деревья способны понизить температуру на несколько градусов Цельсия, за счет создания тени для наших домов и улиц, разбивая городские «тепловые острова» и выпуская водяной пар в воздух через листья.

#5: Экономят энергию

Три дерева, правильно размещенные вокруг дома, могут сократить летние потребности в кондиционировании воздуха на 50 %. При снижении спроса на энергию, для охлаждения наших помещений, уменьшаются выбросы двуокиси углерода и других загрязняющих веществ от электростанций.

#6: Экономят воду

Многим саженцам нужно около 15 галлонов воды в неделю. Тень от деревьев замедляет испарение воды из почвы и увеличивает влагу в атмосфере.

#7: Предотвращают загрязнение воды

Деревья уменьшают сток, разбивая осадки, что позволяет замедлить скорость потока воды. Это предотвращает попадание загрязняющих веществ и мусора в океан. Еще деревья действуют как губка, которая фильтрует грунтовые воды.

#8: Предотвращают эрозию почвы

Деревья своей корневой системой скрепляют почву, удерживая ее на месте, а также замедляют скорость ветра и поток воды.

#9: Защищают детей от ультрафиолетовых лучей

Рак кожи является самой распространенной формой рака в странах с жарким и солнечным климатом. Деревья снижают воздействие ультрафиолетовых лучей примерно на 50 %, обеспечивая тем самым защиту детей на школьных дворах и детских площадках, где они проводят много времени.

#10: Обеспечивают нас питанием

Яблоня может дать около 400-600 кг плодов в год. Помимо пропитания людей, деревья обеспечивают пищей птиц и диких животных.

#11: Исцеляют

Исследования показали, что пациенты в палатах с видом на деревья выздоравливают значительно быстрее и с меньшим количеством осложнений. У Детей с СДВГ (Синдром дефицита внимания и гиперактивности) было замечено меньшее проявление симптомов заболевания, когда они имели доступ к природе. Созерцание на зеленые деревья расслабляет и снижает уровень умственной усталости.

#12: Уменьшают насилие

Дома, которые не имеют деревьев, показали значительный уровень насилия среди их владельцев, чем их озелененные аналоги. Еще деревья помогают уменьшить уровень страха.

#13: Дают представление о времени года

Это зима, весна, лето или осень? Взгляните на деревья и сразу станет ясно!

#14: Создают экономические возможности

Фрукты, собранные в саду можно продать, тем самым обеспечив доход. Неплохие перспективы для зеленого бизнеса возникают в городах, которые в наше время нуждаются в озеленении, как никогда раньше. Профессиональные курсы обучения людей, заинтересованных в работе по озеленению, также являются отличным способом получения экономической выгоды.

#15: Учителя и товарищи по играм

Дома для детей или места творческого и духовного вдохновения для взрослых. Деревья предоставляют нам уютное пространство для игр, общения, работы или учебы.

#16: Объединяют различные группы людей вместе

Посадка молодых деревьев предоставляет возможность участия групп людей различных возрастов, полов и взглядов в коллективных мероприятиях, что улучшает взаимопонимание и приводит к новым интересным знакомствам.

#17: Служат защитой и средой обитания для животных

Дуб и каштан являются одними из многочисленных видов городских деревьев, которые обеспечивают жильем и укрытием насекомых, птиц, белок и других животных.

#18: Украшают

Деревья могут маскировать неприглядные виды, а также приглушать звуки и создавать приятный, и успокаивающий зеленый занавес для глаз.

#19: Обеспечивают древесиной

В пригородных и сельских районах, древесина может быть использована в качестве топлива для обогрева помещений или приготовления пищи.

#20: Увеличивают стоимость недвижимости

Красота от хорошо посаженых и ухоженных деревьев около дома может поднять его стоимость на целых 15 %.

Источник

5.14. Деревья и их свойства

– замкнутые цепи_.

_{2. Любые 2 вершины v и w соединены единственной цепью.}

_{Доказательство следует из определения дерева.}

_{3. Для дерева справедливо следующее соотношение: p = q + 1 (*), где p – число вершин, q – число ребер.}

_{Доказательство (индукцией по p):}

_{а) p = 1 – дерево состоит из одной вершины, q = 0, тогда соотношение (*) выглядит 1 = 1.}

_{б) Пусть соотношение (*) верно для любых деревьев, у которых вершин меньше, чем p.}

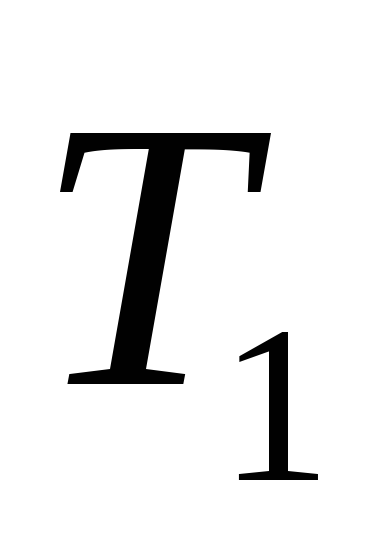
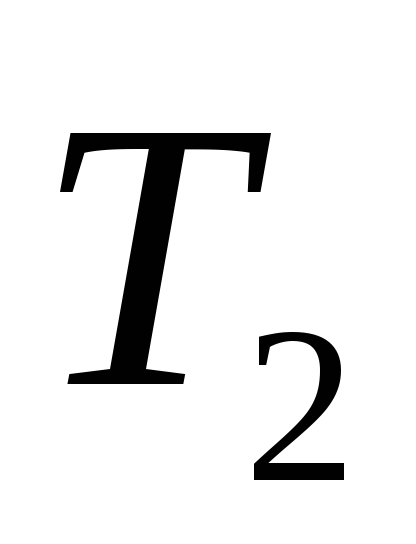
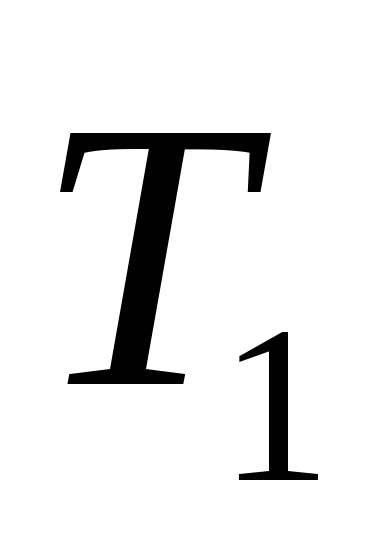
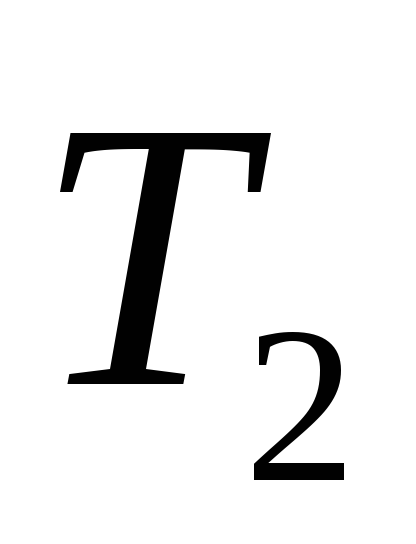
_{в) Рассмотрим дерево с p вершинами. Уберем ребро, соединяющее вершины v и w. Наш граф разбился на 2 подграфа и . , – деревья, так как они связны и не имеют замкнутых цепей. Поэтому для них верно индукционное предположение:}

_{VWV W}

_.

_{4. Если любые 2 вершины v и w в дереве соединить ребром, то получим ровно одну замкнутую цепь.}

_{Доказательство следует из свойства 2.}

_{5. Пусть G = (p, q) – дерево, где p > 1. Тогда в дереве G существуют хотя бы 2 вершины v и w такие, что .}

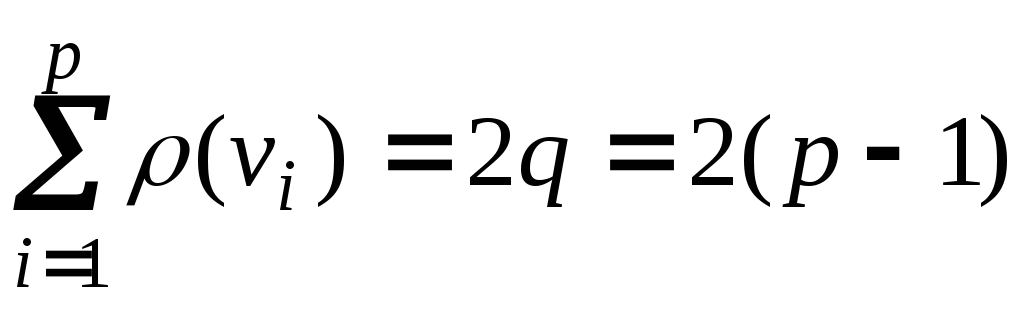
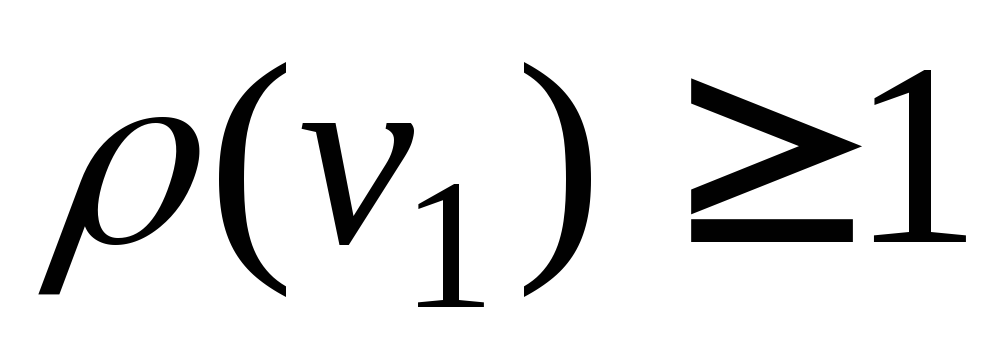
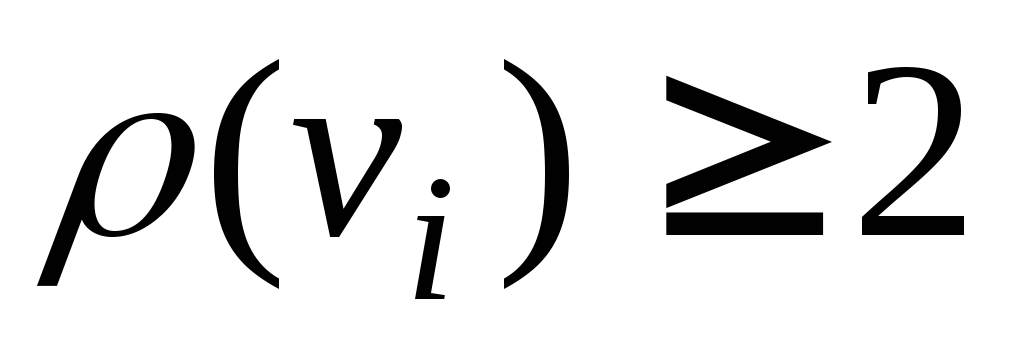
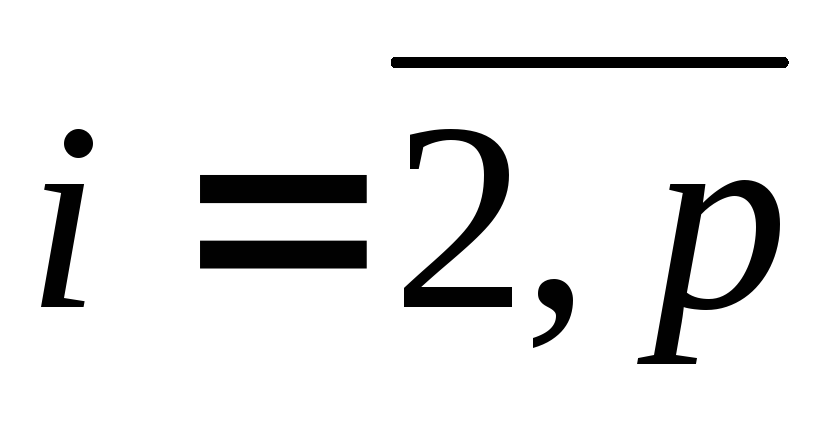
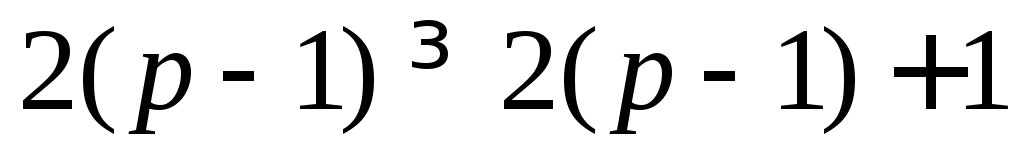
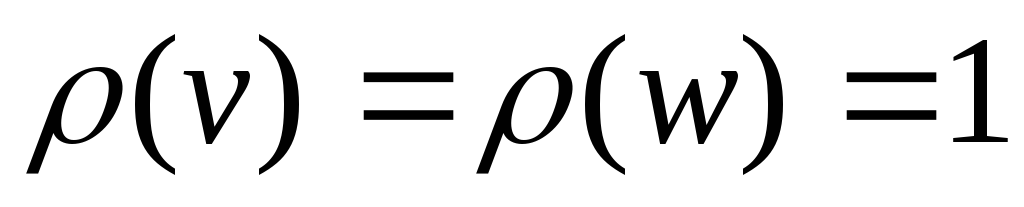
_{Доказательство. Как известно, (по свойству 3). Предположим, что не существуют 2 вершины, степень которых равна 1, т.е. пусть , а у остальных вершин , где . Тогда получаем, что . Пришли к противоречию, значит, существуют вершины v и w такие, что .}

_{Определение. Вершины в дереве, степень которых равна 1, называются концевыми.}

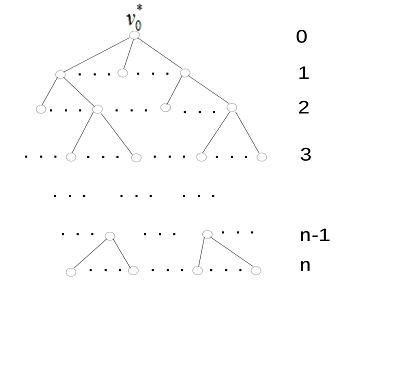
_{где max(n) – глубина (количество ярусов) дерева, – корень дерева (корень – это некоторая выделенная вершина).}

5.15. Деревья и операции над ними

_{1. Ребро – дерево с корнем (код 01), дереву из одного ребра дается код 01.}

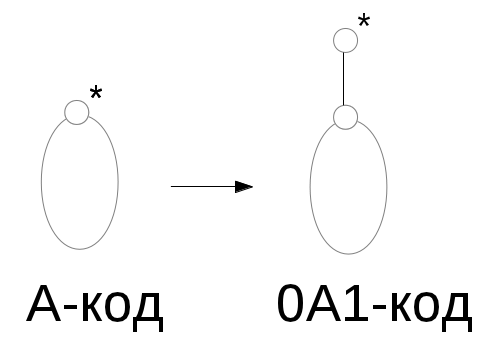
_{2. Если у нас есть дерево с корнем, то результат присоединения этого дерева к ребру – также есть дерево с корнем.}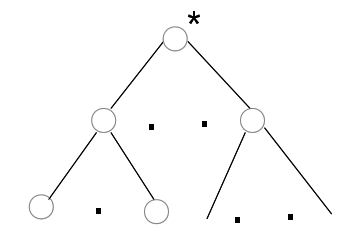

_{При этом пусть дерево с корнем имеет код А, тогда дереву, полученному в результате операции 2, ставится код 0А1.}

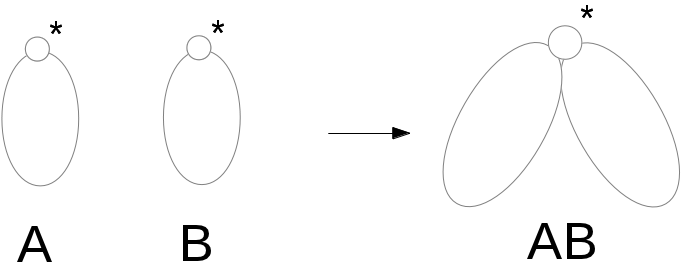
_{3. Если у нас есть два дерева с корнем,}

_{то результат склеивания этих деревьев также есть дерево с корнем. Если при этом у одного дерева код А, а у другого код В, тогда у дерева, которое получается склеиванием этих деревьев, код будет АВ.}

_{Замечание. Любое дерево с корнем можно получить при помощи вышеуказанных трех операций, при этом всегда можно определить его код.}

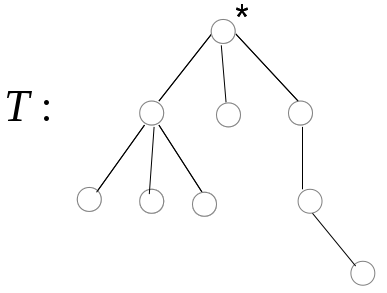
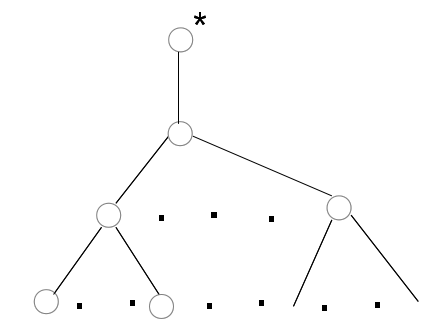
_{Пример. Пусть дано корневое дерево Т, определить его код, где}

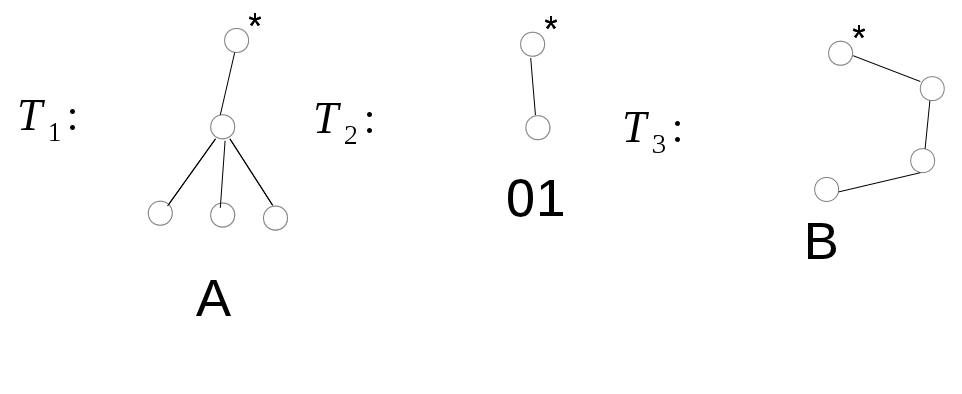
_{Решение: Исходное дерево Т получено из деревьев двукратным применением операции 3, где}

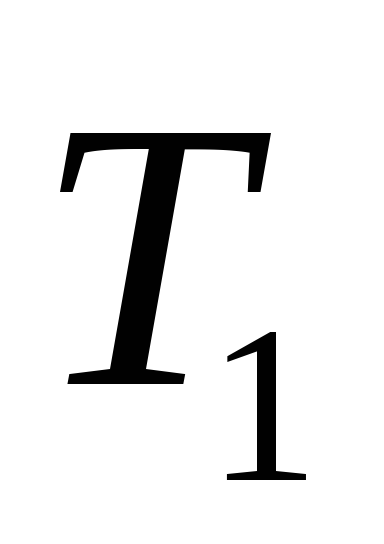
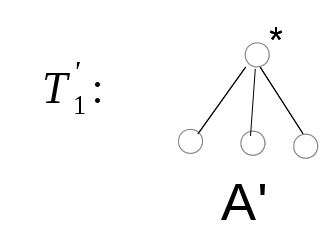
_{1) Дерево получено из дерева с помощью операции 2, где}

_,

_{Дерево получено из дерева операции 1 двукратным применением}

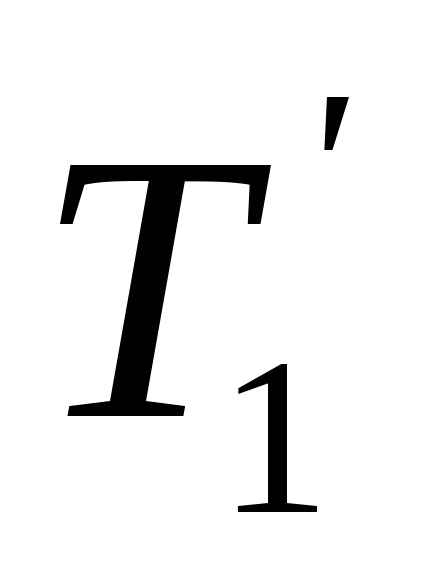
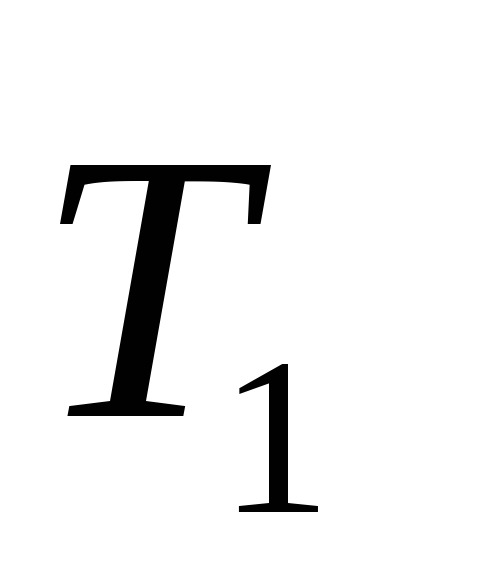
_{операции 3, тогда код дерева A‘ = 010101, следовательно, код дерева A = 00101011.}

_{2) Дерево Т2 получено с помощью операции 1, его код – 01.}

_{3) Дерево Т3 получено из дерева операции 1 двукратным применением операции 2, тогда код дерева Т3 В = 000111.}

_{В итоге код корневого дерева Т есть код А01В = 0010101101000111.}

_{1) Длина кода дерева равна удвоенному числу его ребер (2q).}

_{2) В любом начальном отрезке (если считать код дерева слева) число нулей числа единиц.}

_{3) Во всем коде число нулей равно числу единиц.}

_{Встает логичный вопрос: как восстанавливать по коду дерево?}

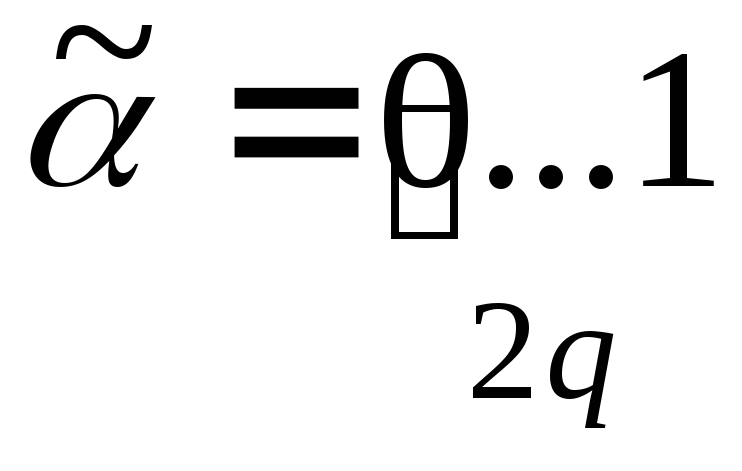
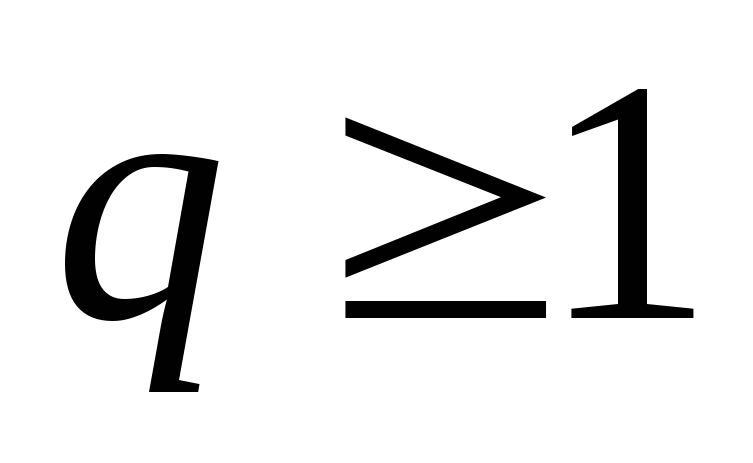
_{Берем произвольный код дерева, где , q – число ребер дерева. Идем слева направо и отмечаем такой момент, когда число нулей совпадает с числом 1. При этом возможны два случая:}

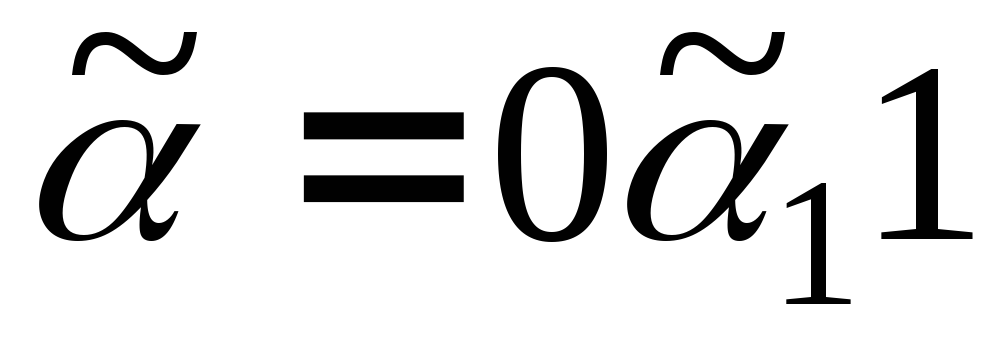
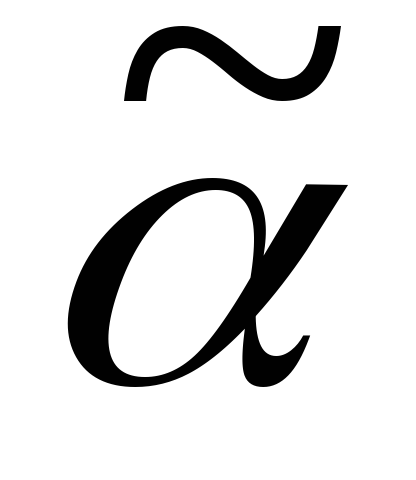
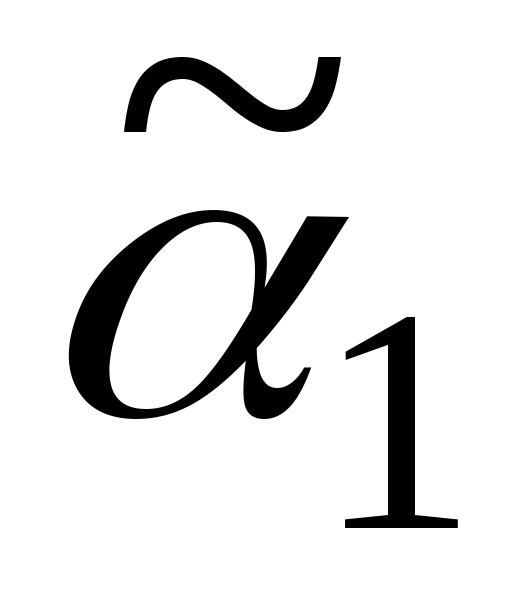
_{1) Пусть равенство наступит в конце кода, тогда , т.е. дерево с кодом получено из дерева с кодом с помощью операции 2.}

_{2) Пусть равенство наступит, не доходя до конца кода, т.е. , а это означает, что дерево с кодом получено из деревьев соответственно с кодами и с помощью операции 3.}

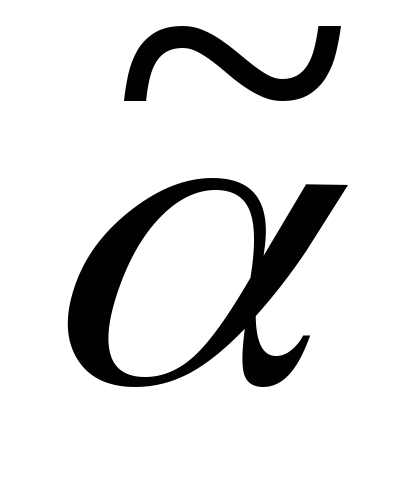
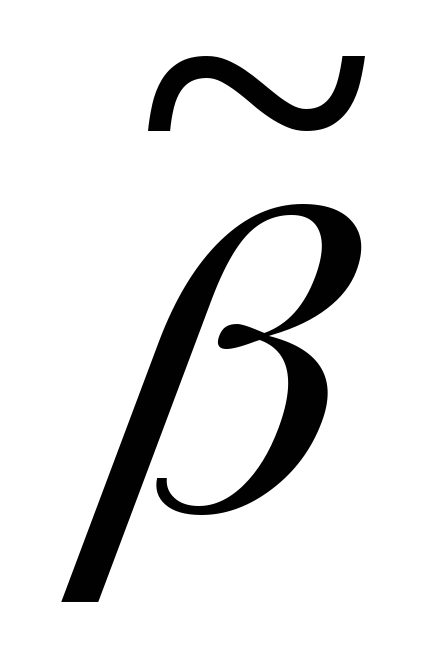
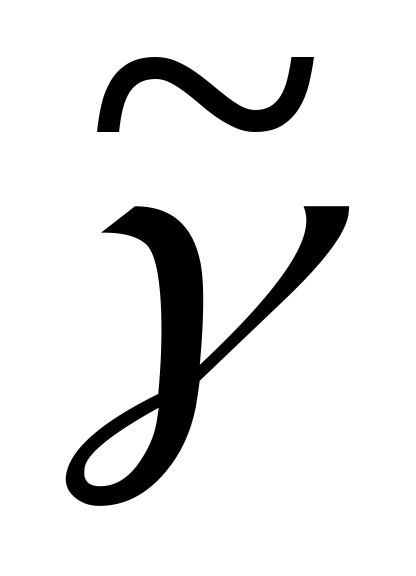
_{Аналогично, т.е. согласно пунктам 1) и 2), восстанавливаем по кодам соответствующие им деревья. Этот процесс называется декодированием. Не сложно доказать (мы практически уже показали), что между деревом и его кодом существует взаимно однозначное соответствие.}

_{Пример. Построить корневое дерево по его коду .}

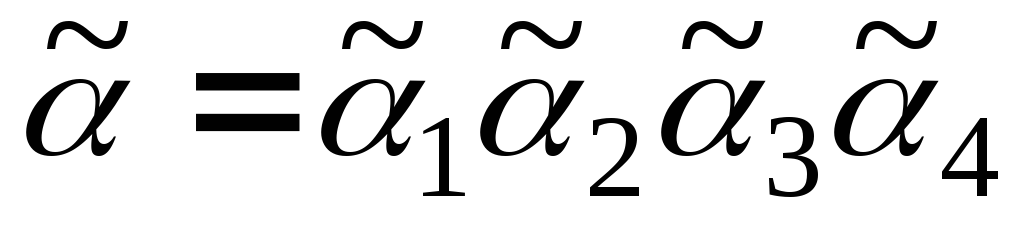
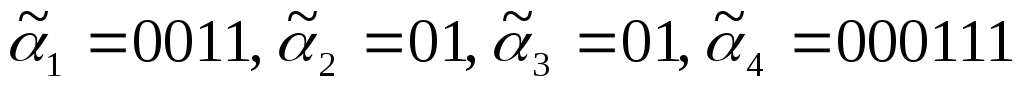
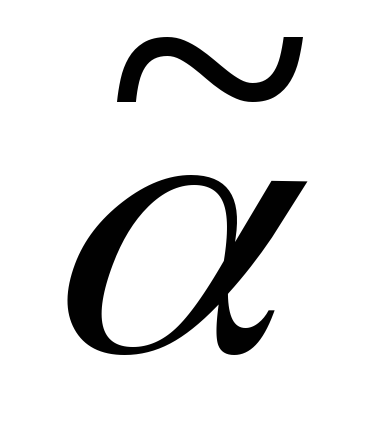
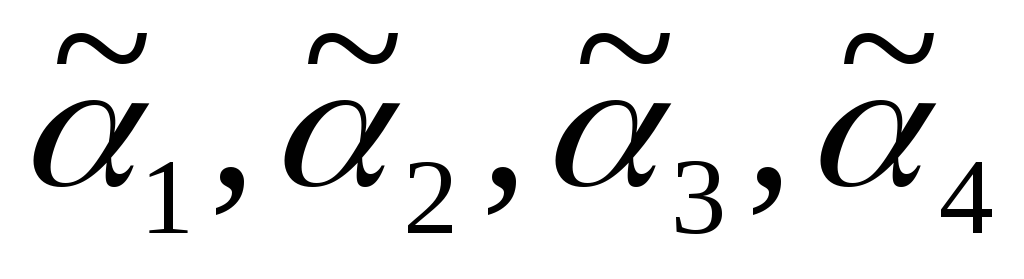
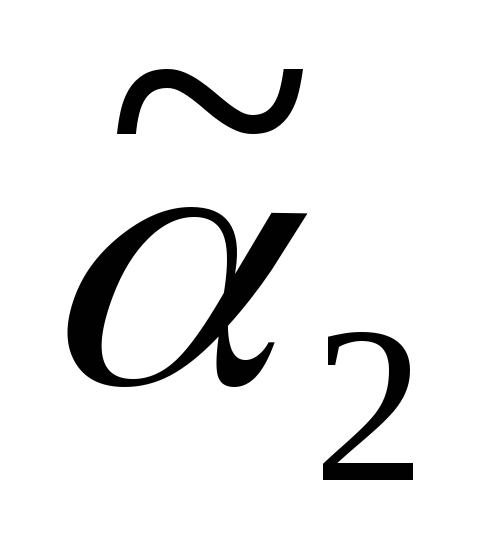
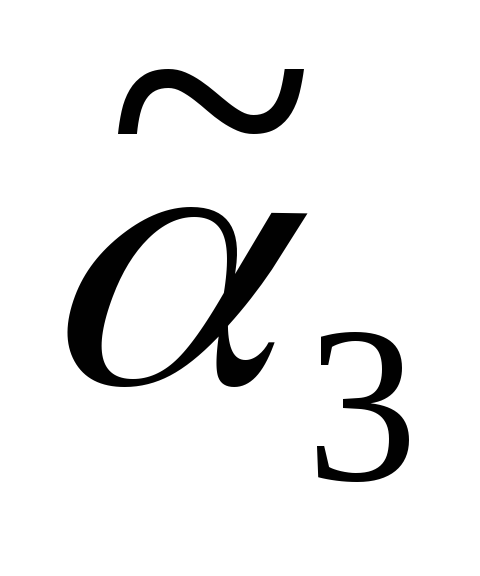
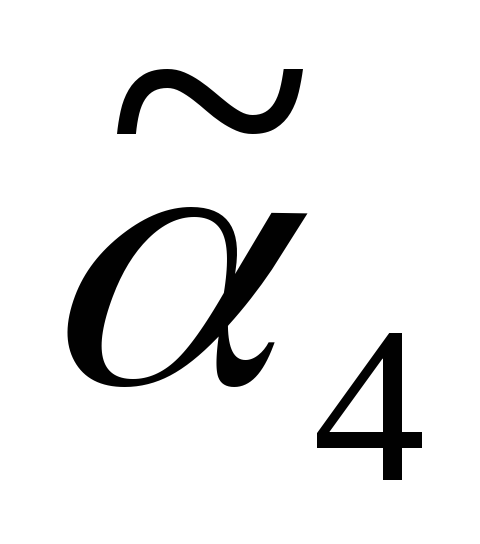
_{Решение: q = 7. , где . Таким образом, дерево с кодом получено из деревьев соответственно с кодами с трехкратным применением операции 3. Аналогично, дерево с кодом получено из дерева операции 1 с применением операции 2; деревья с кодами и – деревья операции 1; дерево с кодом получено из дерева операции 1 с двукратным применением операции 2. В итоге дерево Т выглядит следующим образом:}

Источник