71. Теория графов. Основные понятия. Решаемые задачи.
Тео́рия гра́фов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами. В строгом определении графом называется такая пара множеств. G = (V, E), где V есть подмножество любого счётного множества, а E — подмножество V \times V.
Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.
Основные понятия теории графов
- Граф — система, которая интуитивно может быть рассмотрена как множество точек и множество соединяющих их линий (рис. 1).
- Точки называются вершинами графа, линии со стрелками — дугами, без стрелок — ребрами. Граф, в котором направление линий не выделяется (все линии являются ребрами), называется неориентированным, граф, со стрелками (линии являются дугами) называется ориентированным.
- Подграфом называется часть графа, образованная подмножеством вершин вместе со всеми ребрами (дугами), соединяющими вершины из этого множества. Если из графа удалить часть ребер (дуг), то получим частичный граф.
- Две вершины называются смежными, если они соединены ребром (дугой). Смежные вершины называются граничными вершинами соответствующего ребра (дуги), а это ребро (дуга) — инцидентным соответствующим вершинам.
- Путем называется последовательность дуг (в ориентированном графе), такая, что конец одной дуги является началом другой дуги.
- Простой путь — путь, в котором ни одна дуга не встречается дважды.
- Элементарный путь — путь, в котором ни одна вершина не встречается дважды.
- Контур — путь, у которого конечная вершина совпадает с начальной вершиной.
- Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).
- Замкнутая цепь называется циклом.
- Элементарная цепь (цикл, путь, контур), проходящая через все вершины графа называется гамильтоновой цепью (соответственно – циклом, путем, контуром).
- Простая цепь (цикл, путь, контур), содержащая все ребра (дуги) графа называется эйлеровой цепью (соответственно – циклом, путем, контуром).
- В неориентированном графе степенью вершины i называется число инцидентных ей ребер. Очевидно, . Граф, степени всех вершин которого равны n – 1, называется полным. Граф, все степени вершин которого равны, называется однородным.
- Вершина, для которой не существует инцидентных ей ребер ( = 0) называется изолированной. Вершина, для которой существует только одно инцидентное ей ребро ( = 1) называется висячей.
- Определим матрицу смежностиграфа как квадратную матрицу n ×n, элемент которой равен единице, если (i, j) V, и нулю, если (i, j) V, i, j X. Для неориентированного графа матрица смежности всегда симметрическая.
- Деревом называется связный граф без простых циклов, имеющий не менее двух вершин. Для дерева m = n – 1, а число висячих вершин равно Легко показать, что в дереве любые две вершины связаны единственной цепью.
- Плоским(планарным) называется граф, который можно изобразить на плоскости так, что различным вершинам соответствуют различные кружки и никакие два ребра не имеют общих точек, отличных от их границ (не пересекаются). Для плоского графа существует понятие грани – части плоскости, ограниченной ребрами и не содержащей внутри себя ни вершин, ни ребер.
- Степенью грани называется число ее граничных ребер (висячие ребра считаются дважды).
- Любому связному плоскому графу G можно поставить в соответствие двойственный ему связный плоский граф G*, определяемый следующим образом: каждой грани графа G соответствует вершина графа G*, каждому ребру V графа G, являющемуся граничным для граней z1 и z2, соответствует ребро V* графа G*, соединяющее соответствующие граням z1 и z2 вершины.
Некоторые задачи теории графов
- Планарность графа — можно ли изобразить граф на плоскости без пересечений ребер (или с минимальным числом слоев, что находит применение при трассировке межсоединений элементов печатных плат или микросхем).
К теории графов также относится целый ряд математических проблем, не решенных на сегодняшний день.
- В химии (для описания структур, путей сложных реакций, правило фаз также может быть интерпретировано как задача теории графов); компьютерная химия — сравнительно молодая область химии, основанная на применении теории графов. Теория графов представляет собой математическую основу хемоинформатики. Теория графов позволяет точно определить число теоретически возможных изомеров углеводородов и других органических соединений.
- В информатике и программировании (граф-схема алгоритма)
- В коммуникационных и транспортных системах. В частности, для маршрутизации данных в Интернете.
- В экономике
- В логистике
- В схемотехнике (топология межсоединений элементов на печатной плате или микросхеме представляет собой граф или гиперграф).
Источник
3. Элементы теории графов
Графы возникли в XVIII столетии, когда известный математик, Леонард Эйлер пытался решить теперь уже классическую задачу о Кёнигсбергских мостах. В то время в городе Кёнигсберге (Калининград) было два острова, соединенных семью мостами с берегами реки Преголь и друг с другом.
Задача состояла в том, что необходимо было совершить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка.
В 1736 г. Эйлер показал, что сделать это невозможно.
С тех пор поток задач с применением графов нарастал. Однако теория графов как математическая дисциплина сформировалась только в середине 30-х гг. XX в. благодаря работам таких математиков, как Г. Кёниг, Л.С. Понтрягин, А.А. Зыков и др.
Впервые же понятие «граф» ввел венгерский математик Д. Кёниг в 1936 г.
С графами, сами того не замечая, мы сталкиваемся постоянно. Например, графом является схема движения автобуса. Точками на ней представлены остановки, а линиями – пути движения автобуса. Исследуя свою родословную и возводя ее к далекому предку, мы строим так называемое генеалогическое дерево. И это дерево – граф. Применяются графы для решения задач химии, экономики, электротехники и автоматики, также широко используются в информатике и строительстве. Без графов сложно анализировать классификации в различных науках.
Определение 1. Неориентированным графом (или графом)
называется совокупность двух множеств – непустого множества
(множества вершин) и множества
неупорядоченных пар различных элементов множества
(
–множество ребер).
Обычно граф изображают в виде диаграммы, на которой вершины обозначаются точками, а ребра, соединяющие две вершины, – линиями между этими точками.
Например, изображение графа с множеством вершин
и множеством ребер
может иметь следующий вид (рис. 12).
Изображение графа с множеством вершин
и множеством ребер
может иметь вид, представленный на рис. 13.
Определение 2. Пусть
– вершины,
– соединяющее их ребро. Тогда вершина
и ребро
инцидентны, вершина
и ребро
такжеинцидентны, при этом
называютсяконцами ребра. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
Определение 3. Ребро, соединяющее вершину саму с собой, называют петлей. Ребра, инцидентные одной и той же паре вершин, называются параллельными, или кратными.
Определение 4. Степенью вершины
называется удвоенное количество петель, инцидентных этой вершине, плюс количество остальных инцидентных ей ребер. Обозначение:
. Вершина степени 0 называетсяизолированной, а степени 1 – висячей (концевой). Ребро, инцидентное висячей вершине, называют концевым.
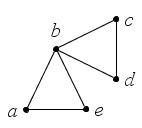
Например, в графе (рис. 14) вершины
и
– смежные,
и
инцидентны ребру
и являются его концами;
– смежные ребра; вершины
и
не являются смежными, поскольку между ними есть вершина
,
и
– не являются смежными ребрами:
,
.
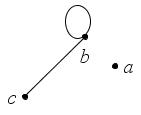
В графе (рис. 15) вершина
– изолированная, вершина
– висячая; ребро, соединяющее вершину
саму с собой, образует петлю:
,
,
.
Теорема 1. Сумма степеней вершин графа всегда четная.
Теорема 2. Сумма степеней всех вершин графа равна удвоенному числу ребер, т. е.
, где
– число ребер.
Определение 5. Ребро, имеющее направление от одной вершины к другой, называется направленным (или ориентированным, или дугой) и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом. Граф, содержащий направленные ребра, называется ориентированным графом (или орграфом).
Замечание 1. В орграфе у каждой вершины две степени: входящая (число ребер, входящих в вершину) и исходящая (число ребер, выходящих из вершины). Петля несет вклад в обе степени по одному.
Например, изображение орграфа
(рис. 16) с множеством вершин
и множеством дуг
.
Дуга
: 1 – начало дуги, 2 – конец дуги;
– петля; ребра
,
– кратные:
,
,
,
,
.
Определение 6. Чередующаяся последовательность вершин и ребер
в графе (или только ребер), в которой любые два элемента инцидентны, называется маршрутом. Количество ребер
, входящих в маршрут, называютдлиной маршрута.
Определение 7. Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называется простой цепью.
Определение 8. Замкнутая цепь называется циклом, а замкнутая простая цепь – простым циклом.
Определение 9. Цикл, который содержит все ребра графа, называется эйлеровым циклом. Простой цикл, содержащий все вершины графа, называется гамильтоновым.
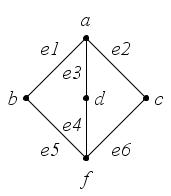
Например, в графе (рис. 17):
–маршрут, но не цепь (длина – 3);
–цепь, но не простая цепь (длина – 5);
–простая цепь (длина – 4);
–цикл, но не простой цикл (длина – 6);
–простой цикл (длина – 3).
Определение 10. Для орграфов цепь называется путем, а цикл – контуром.
Например, в орграфе (рис. 18):
и
– пути;
–контур.
- мультиграф – граф, содержащий кратные ребра;
- граф с петлями – граф, содержащий петли (рис. 15);
- псевдограф – граф, содержащий как петли, так и кратные ребра (рис. 16);
- простой граф – граф без петель и кратных ребер (рис. 14);
- полный граф – простой граф, в котором каждая пара вершин соединена ребром (рис. 19);
- дерево – простой граф, не содержащий циклов;
- эйлеровый граф – граф, содержащий эйлеровый цикл;
- гамильтоновый граф – граф, содержащий гамильтоновый цикл.
Рис. 19 Вопросы и задачи для самостоятельного решения 1. Для следующего графа (рис. 20): а) выпишите смежные вершины и смежные ребра; б) выпишите вершины с инцидентными ребрами; в) определите степени каждой вершины графа; г) укажите, как называются вершины
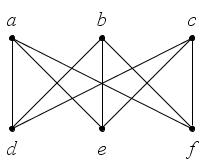
; ребраV и VI; д) укажите, как называется такой граф. 2. Для следующих графов определите, чем являются последовательности ребер и вершин. 2.1. Для графа на рис. 21: а)
; в)
; б)
; г)
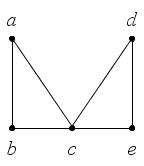
. 2.2. Для графа на рис. 22: а)
; в)
; б)
; г)
. 2.3. Для графа на рис. 23:
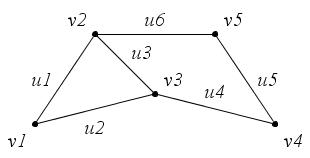
. 3. Для следующего графа (рис. 24): а) выпишите степени всех вершин; б) определите, чем являются последовательности ребер и вершин: 1, 2, 1, 3, 4 и 1, 2, 4.
Рис. 20 Рис. 21 Рис. 22 Рис. 23 Рис. 24 - Найдите эйлеровый граф (рис. 25).
а
бв Рис. 25
Источник








 называется совокупность двух множеств – непустого множества
называется совокупность двух множеств – непустого множества 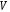 (множества вершин) и множества
(множества вершин) и множества 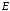 неупорядоченных пар различных элементов множества
неупорядоченных пар различных элементов множества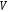 (
(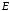 –множество ребер).
–множество ребер).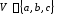 и множеством ребер
и множеством ребер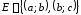 может иметь следующий вид (рис. 12).
может иметь следующий вид (рис. 12).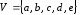 и множеством ребер
и множеством ребер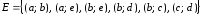 может иметь вид, представленный на рис. 13.
может иметь вид, представленный на рис. 13.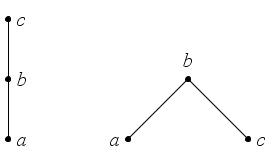
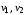 – вершины,
– вершины,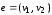 – соединяющее их ребро. Тогда вершина
– соединяющее их ребро. Тогда вершина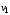 и ребро
и ребро инцидентны, вершина
инцидентны, вершина 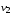 и ребро
и ребро такжеинцидентны, при этом
такжеинцидентны, при этом 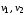 называютсяконцами ребра. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными.
называютсяконцами ребра. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. называется удвоенное количество петель, инцидентных этой вершине, плюс количество остальных инцидентных ей ребер. Обозначение:
называется удвоенное количество петель, инцидентных этой вершине, плюс количество остальных инцидентных ей ребер. Обозначение: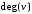 . Вершина степени 0 называетсяизолированной, а степени 1 – висячей (концевой). Ребро, инцидентное висячей вершине, называют концевым.
. Вершина степени 0 называетсяизолированной, а степени 1 – висячей (концевой). Ребро, инцидентное висячей вершине, называют концевым. и
и – смежные,
– смежные, и
и инцидентны ребру
инцидентны ребру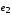 и являются его концами;
и являются его концами;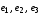 – смежные ребра; вершины
– смежные ребра; вершины и
и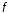 не являются смежными, поскольку между ними есть вершина
не являются смежными, поскольку между ними есть вершина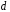 ,
,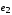 и
и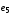 – не являются смежными ребрами:
– не являются смежными ребрами: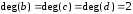 ,
, 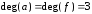 .
. – изолированная, вершина
– изолированная, вершина – висячая; ребро, соединяющее вершину
– висячая; ребро, соединяющее вершину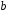 саму с собой, образует петлю:
саму с собой, образует петлю: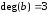 ,
, 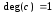 ,
, .
.
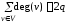 , где
, где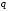 – число ребер.
– число ребер.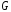 (рис. 16) с множеством вершин
(рис. 16) с множеством вершин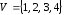 и множеством дуг
и множеством дуг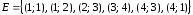 .
.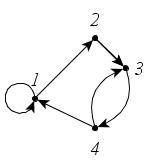
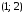 : 1 – начало дуги, 2 – конец дуги;
: 1 – начало дуги, 2 – конец дуги;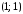 – петля; ребра
– петля; ребра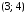 ,
,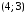 – кратные:
– кратные: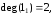
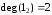 ,
, 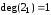 ,
,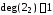 ,
,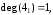
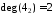 ,
, 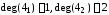 .
.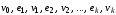 в графе (или только ребер), в которой любые два элемента инцидентны, называется маршрутом. Количество ребер
в графе (или только ребер), в которой любые два элемента инцидентны, называется маршрутом. Количество ребер 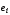 , входящих в маршрут, называютдлиной маршрута.
, входящих в маршрут, называютдлиной маршрута.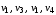
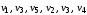
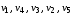
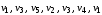
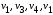
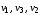 и
и 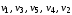 – пути;
– пути;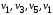
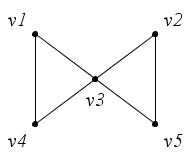
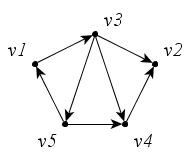
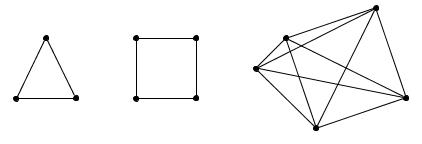 Рис. 19 Вопросы и задачи для самостоятельного решения 1. Для следующего графа (рис. 20): а) выпишите смежные вершины и смежные ребра; б) выпишите вершины с инцидентными ребрами; в) определите степени каждой вершины графа; г) укажите, как называются вершины
Рис. 19 Вопросы и задачи для самостоятельного решения 1. Для следующего графа (рис. 20): а) выпишите смежные вершины и смежные ребра; б) выпишите вершины с инцидентными ребрами; в) определите степени каждой вершины графа; г) укажите, как называются вершины 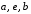 ; ребраV и VI; д) укажите, как называется такой граф. 2. Для следующих графов определите, чем являются последовательности ребер и вершин. 2.1. Для графа на рис. 21: а)
; ребраV и VI; д) укажите, как называется такой граф. 2. Для следующих графов определите, чем являются последовательности ребер и вершин. 2.1. Для графа на рис. 21: а) 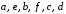 ; в)
; в)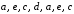 ; б)
; б) 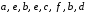 ; г)
; г)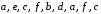 . 2.2. Для графа на рис. 22: а)
. 2.2. Для графа на рис. 22: а) 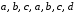 ; в)
; в) ; б)
; б) 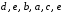 ; г)
; г)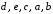 . 2.3. Для графа на рис. 23:
. 2.3. Для графа на рис. 23: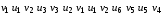 . 3. Для следующего графа (рис. 24): а) выпишите степени всех вершин; б) определите, чем являются последовательности ребер и вершин: 1, 2, 1, 3, 4 и 1, 2, 4.
. 3. Для следующего графа (рис. 24): а) выпишите степени всех вершин; б) определите, чем являются последовательности ребер и вершин: 1, 2, 1, 3, 4 и 1, 2, 4. 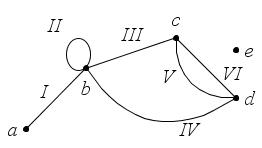

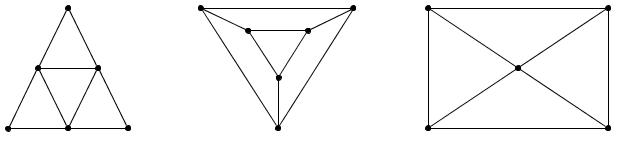 бв Рис. 25
бв Рис. 25