Деревья в языке питон

Бинарное Дерево

Двоичное дерево — древовидная структура данных, в которой у родительских узлов не может быть больше двух детей.

Строим двоичное дерево на Python​

Определим метод __init__() . Как всегда, он принимает self . Также мы передаем в него значение, которое будет храниться в узле. Установим значение узла, а затем определим левый и правый указатель (для начала поставим им значение None).

class TreeNode: def __init__(self, val=0, left=None, right=None):  self.val = val  self.left = left  self.right = right 

И… все! Если речь идет о двоичном дереве, единственное, что его отличает от связного списка, это то, что вместо next у нас тут есть left и right.

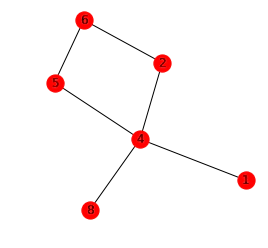
Давайте построим дерево, которое изображено на схеме в начале статьи. Верхний узел имеет значение 1. Далее мы устанавливаем левые и правые узлы, пока не получим желаемое дерево.

tree = TreeNode(1) tree.left = TreeNode(2) tree.right = TreeNode(3) tree.left.left = TreeNode(4) tree.left.right = TreeNode(5) 

Создание дерева из list​

def from_list(l):  nodes = [TreeNode(v) for v in l]  kids = nodes[::-1]  root = kids.pop() for node in nodes: if node: if kids:  node.left = kids.pop() if kids:  node.right = kids.pop() return root t = TreeNode.from_list([4,2,7,1,3,6,9]) print(t) 

def creatBTree(data, index):  pNode = None if index  len(data): if data[index] == None: return  pNode = TreeNode(data[index])  pNode.left = creatBTree(data, 2 * index + 1) # [1, 3, 7, 15, . ]  pNode.right = creatBTree(data, 2 * index + 2) # [2, 5, 12, 25, . ] return pNode lst = [5,4,8,11,None,13,4,7,2,None,None,None,1] root = creatBTree(lst, 0) 

Обход двоичного дерева​

Итак, вы построили дерево и теперь вам, вероятно, любопытно, как же его увидеть. Нет никакой команды, которая позволила бы вывести на экран дерево целиком, тем не менее мы можем обойти его, посетив каждый узел. Но в каком порядке выводить узлы?

Самые простые в реализации обходы дерева

Вы также можете услышать такие термины, как поиск в ширину и поиск в глубину, но их реализация сложнее, ее мы рассмотрим как-нибудь потом.

Итак, что из себя представляют три варианта обхода, указанные выше? Давайте еще раз посмотрим на наше дерево.

При прямом обходе мы посещаем родительские узлы до посещения узлов-потомков. В случае с нашим деревом мы будем обходить узлы в таком порядке: 1, 2, 4, 5, 3.

Обратный обход двоичного дерева — это когда вы сначала посещаете узлы-потомки, а затем — их родительские узлы. В нашем случае порядок посещения узлов при обратном обходе будет таким: 4, 5, 2, 3, 1.

При центрированном обходе мы посещаем все узлы слева направо. Центрированный обход нашего дерева — это посещение узлов 4, 2, 5, 1, 3.

Давайте напишем методы обхода для нашего двоичного дерева.

Прямой обход (Pre-Order)​

Написать обход просто. Прямой обход — это посещение родительского узла, а затем каждого из его потомков. Мы «посетим» родительский узел, выведя его на экран, а затем «обойдем» детей, вызывая этот метод рекурсивно для каждого узла-потомка.

# Выводит родителя до всех его потомков def pre_order(node): if node: print(node.value)  pre_order(node.left)  pre_order(node.right) 

Дополнительные ссылки​

Источник

Напишем и поймем Decision Tree на Python с нуля! Часть 4. Структуры данных

Структура данных — это представление того, как организованы отдельные данные.

Массив

Отдельные данные представлены одним рядом. Чтобы идентифицировать один фрагмент данных, например, каким по порядку является этот отдельный фрагмент массива, необходим его идентификатор.

#Пример реализации массива в Python a = [2,6,4,5,1,8]

Таблица, двумерный массив

Данные выстроены в несколько столбцов, отдельные элементы двумерного массива также образуют строки.

Чтобы идентифицировать фрагмент данных в этом случае, требуются два идентификатора: например, номер столбца и номер элемента.

#Пример реализации таблицы в Python a = [ [2,6,4,5,1,8], [4,4,1,3,4,2], [5,3,6,6,5,3], [7,8,0,9,5,3], ]

Tree, древовидная структура

Это структура данных, где отдельные данные как будто связаны линией.

Эти линии являются маршрутом, напрямую соединяющим одни данные с другими. И один такой маршрут, например, и будет являтся древовидной структурой данных.

Часто такую структуру изображают как схему, напоминающую растущее сверху вниз дерево. Линии называются ребрами или ветвями, данные — узлами (node), данные, после которых линия не продолжается, называются листьями(leaf), а данные, располагающиеся на самом верху — корневым узлом или просто корнем.

# Пример реализации Tree в Python, содержащий список дочерних узлов. # Записывается в формате [Значение,список дочерних массивов]. Например, дерево с картинки выше будет записываться в порядке сверху вниз, слева направо. # Помимо подобной записи, существуют варианты с использованием классов, родительских нодов и другие. tree = \ [2,[ [6,[]], [4,[ [5,[ [6,[]], ]], [8,[]], [1,[]], ]], ]] # Функция для преобразования древовидной структуры в символьную def tstr(node,indent=""): s = indent+str(node[0])+"\n" for c in node[1]: # Цикл на дочернем ноде s += tstr(c,indent+"+-") pass return s print(tstr(tree)) # Вывод # 2 # +-6 # +-4 # +-+-5 # +-+-+-6 # +-+-8 # +-+-1 # Можно не создавать все дерево сразу, а создать несколько переменных для нодов # Создаем все ноды-листья. Цифра в переменной указывает на строку нода и его порядковый номер в этой строке слева направо. n10 = [6,[]] n21 = [8,[]] n22 = [1,[]] n40 = [6,[]] # Создаем родительские ноды для уже созданных дочерних. n20 = [5,[n40]] n11 = [4,[n20,n21,n22]] n00 = [2,[n10,n11]] # Выводим получившееся Древо, указав нод, который необходимо считать корневым. print(tstr(n11)) # Вывод # 4 # +-5 # +-+-6 # +-8 # +-1

Network или графы

Это структура, в которой у одного нода может быть несколько ребер. Отдельные данные также называются узлами, а линии — ребрами. Зачастую в графах нет корневого узла, как в древовидной структуре.

# Реализация графа на Python import pandas as pd # В нашем случае имя узла и его значение совпадают. # Если имя нода и его значение не совпадают, необходимо будет достать значение нода. nodes = [2,6,4,5,8,1] # Указываем связи между нодами в виде матрицы. Если от нода 2 (первая строка)к ноду 6 (вторая строка) исходит ребро, # Значение 1-ой строки 2-ого столбца матрицы будет 1, а если ребро не проходит, то - 0. Такая матрица называется матрица смежности. df = pd.DataFrame( [ # 2,6,4,5,8,1 [ 0,1,1,0,0,0], # от нода 2 [ 1,0,0,1,0,0], # от нода 6 [ 1,0,0,1,1,1], # от нода 4 [ 0,1,1,0,0,0], # от нода 5 [ 0,0,1,0,0,0], # от нода 8 [ 0,0,1,0,0,0], # от нода 1 ],columns=nodes,index=nodes) print(df) # Вывод # 2 6 4 5 8 1 # 2 0 1 1 0 0 0 # 6 1 0 0 1 0 0 # 4 1 0 0 1 1 1 # 5 0 1 1 0 0 0 # 8 0 0 1 0 0 0 # 1 0 0 1 0 0 0 # С помощью библиотек matplotlib и networkx рисуем граф. import matplotlib.pyplot as plt import networkx as nx plt.figure(figsize=(4,4)) plt.axis("off") nx.draw_networkx(nx.from_pandas_adjacency(df)) plt.show()

4.2 Пример реализации Decision Tree в Python

Decision Tree, как понятно из названия, может быть представлен в виде древовидной структуры.
В нодах хранятся следующие данные: список дочерних нодов, правила ветвления, путь от одного нода к другому в рамках Decision Tree.

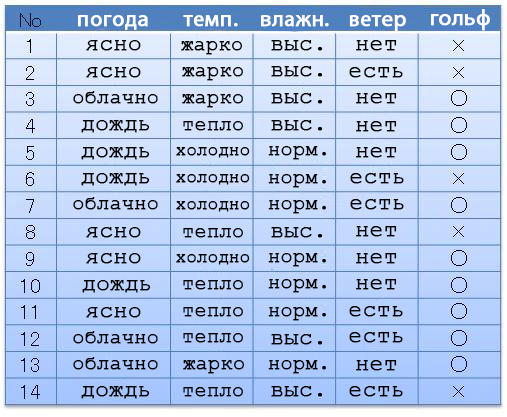
Как показано ниже, корневой узел соединяет все данные. Числовое значение [. ], прикрепленное к узлу, представляет собой номер исходных данных, из которых создается это дерево решений. Из корневого узла “спускаются” вниз только те данные, которые удовлетворяют условиям дочерних узлов. Например, это видно, если посмотреть на узлы “иду на гольф” и “не иду на гольф” в первом дереве решений.

Реализация в python-е происходит, например, следующим образом. Делаем один узел ассоциативным массивом, name — это символьное представление состояния этого узла, df — это данные, связанные с этим узлом, а ребра — это список дочерних узлов.

# Данные древовидной структуры tree =

Функция tstr, текстифицирующая данную древовидную структуру, будет выглядеть следующим образом.

# Лямбда-выражение для распределения значений, аргумент - pandas.Series, возвращаемое значение - массив с количеством каждого из значений # Из вводных данных s с помощью value_counts() находим частоту каждого из значений, и пока в нашем словаре есть элементы, будет работать цикл, запускаемый items(). # Чтобы выходные данные не менялись с каждым запуском цикла, мы используем sorted, который меняет порядок от большего к меньшему # В итоге, генерируется массив, содержащий строку из следующих компонентов: ключ (k) и значение (v). cstr = lambda s:[k+":"+str(v) for k,v in sorted(s.value_counts().items())] # Метод текстификации дерева: аргумент - tree (структура данных дерева), indent (отступ дочерних узлов), # А возвращаемое значение будет текстовым отображением tree. Данный метод вызывается рекурсивно для преобразования всего в дереве в символы. def tstr(tree,indent=""): # Создаем символьное представление этого узла. # Если этот узел является листовым узлом (количество элементов в массиве ребер равно 0), # Частотное распределение последнего столбца данных df, связанных с деревом, преобразуется в символы. s = indent+tree["name"]+str(cstr(tree["df"].iloc[:,-1]) if len(tree["edges"])==0 else "")+"\n" # Зацикливаем все ветви этого узла. for e in tree["edges"]: # Добавляем символьное представление дочернего узла к символьному представлению родительского узла. # Добавляем еще больше символов к indent этого узла. s += tstr(e,indent+" ") pass return s

Decision Tree, текстифицированное функцией tstr, будет выглядеть следующим образом. В корневом узле отображается текст (decision tree Гольф), который мы задали в самом начале при создании переменной tree, а также частотное распределение «иду / не иду на гольф» со всех данных. Каждый узел представленный ниже, отображает правила ветвления, и в случае, если узел оказывается листовым, отображается частотное распределение «иду / не иду на гольф» на основе данных, связанных с этим узлом.

decision tree Гольф ['×:5', '○:9'] Погода=Ясно Влажность=Нормальная['○:2'] Влажность=Высокая['×:3'] Погода=Облачно['○:4'] Погода=Дождь Ветер=Есть['×:2'] Ветер=Нет['○:3']

Мы будем очень рады, если вы расскажете нам, понравилась ли вам данная статья, понятен ли перевод, была ли она вам полезна?

Источник