Деревья виды деревьев информатика

Содержание

Динамические структуры данных: бинарные деревья
Бинарные деревья
Структуры данных: деревья
Деревья
Зачем нужны деревья
Части дерева
Другие понятия
Виды деревьев
Обход дерева
Где используются

Динамические структуры данных: бинарные деревья

Аннотация: В лекции рассматриваются определения, свойства и виды деревьев, элементы, характеристики и способы объявления деревьев в программах, основные операции над элементами деревьев, понятие и виды обходов деревьев, приводятся примеры реализации основных операций над бинарными деревьями в виде рекурсивных функций.

Цель лекции: изучить понятие, формирование, особенности доступа к данным и работы с памятью в бинарных деревьях, научиться решать задачи с использованием рекурсивных функций и алгоритмов обхода бинарных деревьев в языке C++.

Дерево является одним из важнейших и интересных частных случаев графа. Древовидная модель оказывается довольно эффективной для представления динамических данных с целью быстрого поиска информации .

Деревья являются одними из наиболее широко распространенных структур данных в информатике и программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.

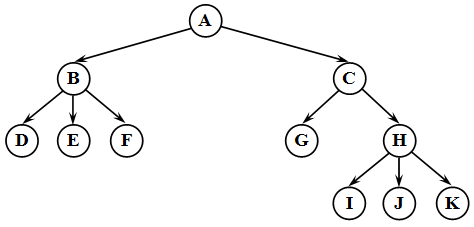
Дерево – это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов ( рис. 31.1). Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.

Каждое дерево обладает следующими свойствами:

существует узел, в который не входит ни одной дуги (корень);
в каждую вершину, кроме корня, входит одна дуга.

Деревья особенно часто используют на практике при изображении различных иерархий. Например, популярны генеалогические деревья.

Все вершины, в которые входят ветви, исходящие из одной общей вершины, называются потомками, а сама вершина – предком. Для каждого предка может быть выделено несколько. Уровень потомка на единицу превосходит уровень его предка. Корень дерева не имеет предка, а листья дерева не имеют потомков.

Высота (глубина) дерева определяется количеством уровней, на которых располагаются его вершины. Высота пустого дерева равна нулю, высота дерева из одного корня – единице. На первом уровне дерева может быть только одна вершина – корень дерева , на втором – потомки корня дерева, на третьем – потомки потомков корня дерева и т.д.

Поддерево – часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.

Степенью вершины в дереве называется количество дуг, которое из нее выходит. Степень дерева равна максимальной степени вершины, входящей в дерево . При этом листьями в дереве являются вершины, имеющие степень нуль. По величине степени дерева различают два типа деревьев:

Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.

Деревья являются рекурсивными структурами, так как каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:

Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.

Списочное представление деревьев основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева .

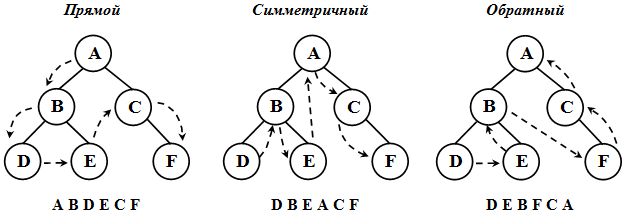
Для того, чтобы выполнить определенную операцию над всеми вершинами дерева необходимо все его вершины просмотреть. Такая задача называется обходом дерева.

Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.

При обходе все вершины дерева должны посещаться в определенном порядке. Существует несколько способов обхода всех вершин дерева. Выделим три наиболее часто используемых способа обхода дерева ( рис. 31.2):

Существует большое многообразие древовидных структур данных. Выделим самые распространенные из них: бинарные (двоичные) деревья, красно-черные деревья, В-деревья, АВЛ-деревья , матричные деревья, смешанные деревья и т.д.

Бинарные деревья

Бинарные деревья являются деревьями со степенью не более двух.

Бинарное (двоичное) дерево – это динамическая структура данных , представляющее собой дерево , в котором каждая вершина имеет не более двух потомков ( рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка .

Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:

информационное поле (ключ вершины);
служебное поле (их может быть несколько или ни одного);
указатель на левое поддерево ;
указатель на правое поддерево .

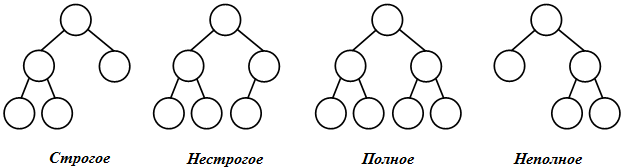
По степени вершин бинарные деревья делятся на ( рис. 31.4):

строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).

В общем случае у бинарного дерева на k -м уровне может быть до 2 k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным.

Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.

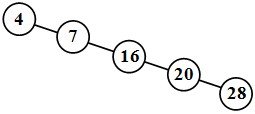
Бинарное дерево может представлять собой пустое множество . Бинарное дерево может выродиться в список ( рис. 31.5).

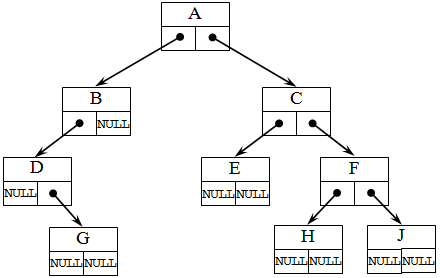
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, ‘*’ (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева , представленного на следующем рисунке 6, входной поток имеет вид: ABD*G***CE**FH**J** .

Бинарные деревья могут применяться для поиска данных в специально построенных деревьях ( базы данных ), сортировки данных, вычислений арифметических выражений , кодирования (метод Хаффмана) и т.д.

Источник

Структуры данных: деревья

Дерево – это конечное множество T , возможно пустое, в противном случае, состоящее из одного или более элементов (узлов или вершин дерева) таких, что:

а) имеется один специально обозначенный элемент, называемый корнем данного дерева;

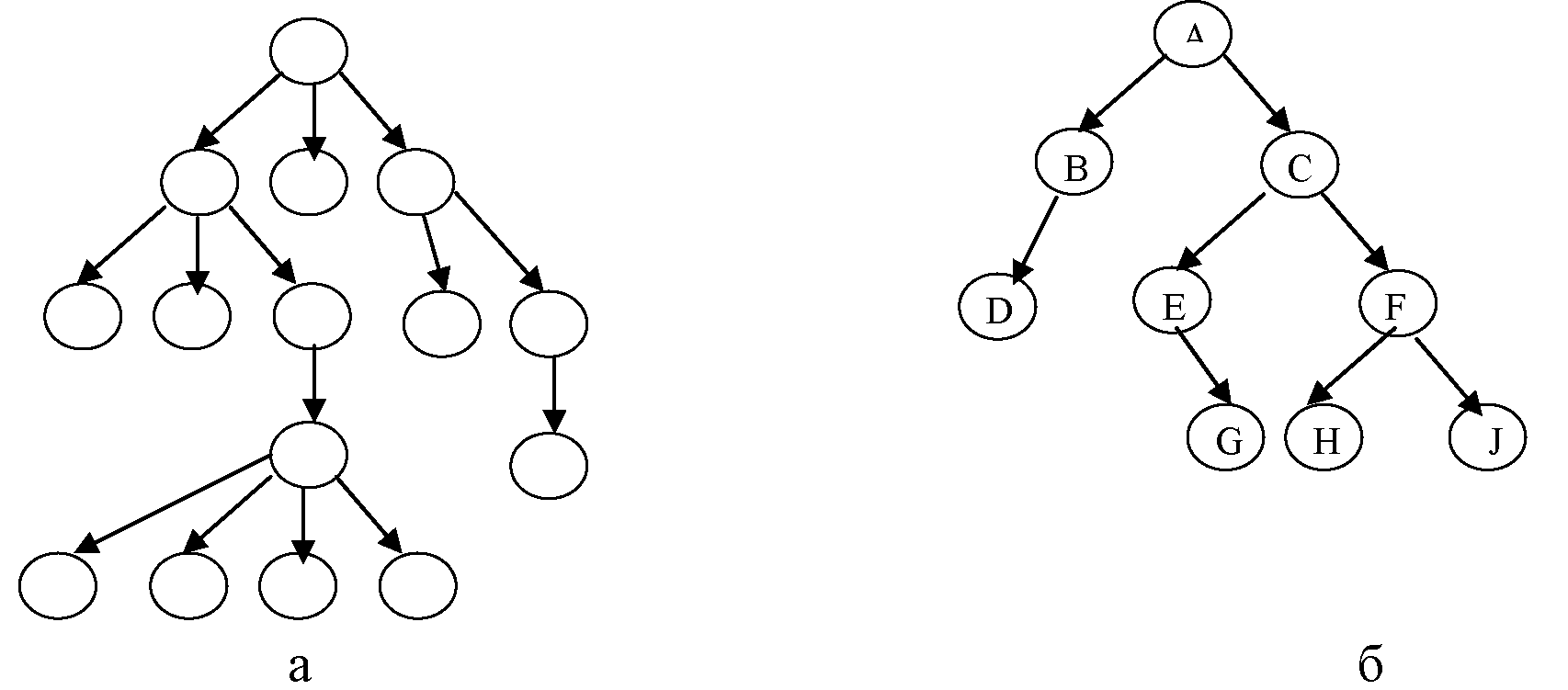
б) остальные элементы содержатся в m >0 попарно непересекающихся множествах T₁ , . . . ,T_m , каждое из которых в свою очередь является деревом; деревья T₁ , . . . , T_m называются поддеревьями данного корня (рис.1.а).

Если имеет значение относительный порядок поддеревьев T₁, . . . ,T_m _, то говорят, что дерево является упорядоченным. Число поддеревьев данного узла называется степенью этого узла. Узел с нулевой степенью называется концевым узлом (или листом или терминальным узлом), все остальные элементы – внутренние узлы (нетерминальные). Максимальная степень всех вершин называется степенью дерева. Корень дерева имеет уровень равный 0. Остальные вершины имеют уровень на единицу больше уровня непосредственного предка. Максимальный уровень какой-либо из вершин называется глубиной или высотой дерева. Минимальная высота при заданном числе вершин достигается, если на всех уровнях, кроме последнего, помещается максимально возможное число вершин. Максимальное число вершин в дереве высотой h достигается в том случае, если из каждой вершины, за исключением уровня h, исходят d поддеревьев, где d –степень дерева: на 0-м уровне 1 вершина, на 1-м – d потомков, на 2-м – d 2 потомков, на 3-м уровне d 3 потомков и т.д.

Наиболее широко используются двоичные (бинарные) деревья (рис.1.б). Бинарное дерево это конечное множество элементов, которое либо пусто, либо состоит из корня и из двух непересекающихся бинарных деревьев, называемых левым и правым поддеревьями данного корня. Таким образом, каждый элемент бинарного дерева имеет 0, 1 или 2 поддерева. Бинарное дерево – упорядоченное дерево, так как в нем различают левое и правое поддеревья.

Определение структуры дерева, данное выше, является рекурсивным и отражает рекурсивную природу самой структуры.

Структуру данных – дерево можно представить как в статической, так и в динамической памяти.

В статической памяти дерево можно представить массивом, для которого определено понятие пустого элемента:

Рис.2. двоичное дерево представленное в виде массива

Вершины двоичного дерева располагаются в массиве следующим образом (см. рис.2.): если k – индекс вершины дерева, то ее потомки находятся в элементах массива с индексами 2k + 1 и 2(k + 1); корень дерева находится в элементе с индексом 0 (при индексации в массиве от 1 до N индексы потомков k-ой вершины: 2k и 2k + 1, корень имеет индекс 1).

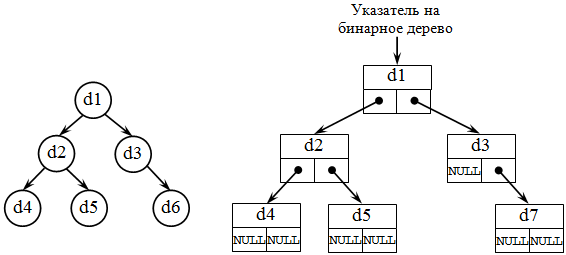
В динамической памяти дерево представляется иерархическим списком. Задать элемент двоичного дерева можно как элемент списка с тремя полями: два ссылочных поля, содержащие указатели на его левое ( L ) и правое ( R ) поддеревья, и информационное поле ( E ):

Определение типа элемента бинарного динамического дерева:

Здесь type – тип информационного поля (если информационное поле имеет сложную структуру, то type может быть типом — указатель на объект, содержащий значение элемента дерева).

Чтобы определить дерево как единую структуру, надо задать указатель на корень дерева:

Рис.3. Двоичное динамическое дерево

На рис.3 представлено двоичное динамическое дерево d в соответствии с определением типа элемента, сделанным выше. Элементы дерева со степенью 0 и 1 имеют два или одно ссылочное поле со значением равным пустому указателю (NULL).

Обрабатывая дерево, приходится просматривать его элементы – эта операция называется обход дерева (или прохождение дерева).

Источник

Деревья

Дерево — это нелинейная иерархическая структура данных. Она состоит из узлов и ребер, которые соединяют узлы.

Зачем нужны деревья

Другие структуры данных, например, массивы, списки, стеки и очереди, линейные. Это значит, что данные в них хранятся последовательно. Когда мы выполняем любую операцию в линейной структуре данных, временная сложность растет с увеличением размера данных. В современном мире это не очень круто.

Разные древовидные структуры позволяют быстрее и легче получать доступ к данным, поскольку дерево — структура нелинейная.

Части дерева

Узел — это объект, в котором есть ключ или значение и указатели на дочерние узлы.
Узлы, у которых нет дочерних узлов, называют листами или терминальными узлами.
Узлы, у которых есть хотя бы один дочерний узел, называются внутренними.
Ребро связывает два узла.
Корень — это самый верхний узел дерева. Его ещё иногда называют корневым узлом.

Другие понятия

Высота узла — это максимальная длина пути от этого узла к самому нижнему узлу (листу).
Глубина вложенности узла — длина пути от корня до этого узла.
Высота дерева — это высота корневого узла или глубина самого глубокого узла.
Степень узла — это общее количество ребер, которые соединены с этим узлом.

Лес — множество непересекающихся деревьев. Например, если «срезать» корень, получится лес.

Виды деревьев

Обход дерева

Чтобы выполнить какую-либо операцию с деревом, нужно добраться до определенного узла. Для этого и существуют алгоритмы обхода дерева. Они помогают «дойти» до необходимого узла.

Где используются

Деревья двоичного поиска помогают быстро проверить наличие элемента в наборе.
Куча — это тоже своеобразное дерево. Кучи используют в алгоритме сортировки кучей.
Префиксные деревья используются в маршрутизаторах, они хранят информацию о маршруте.
Большинство популярных баз данных основаны на B-деревья и T-деревья.
Компиляторы используют абстрактное синтаксическое дерево, чтобы находить синтаксические ошибки в ваших программах.

СodeСhick.io — простой и эффективный способ изучения программирования.

Источник