Создать дерево разбора выражения (инфиксная форма)
Есть образец:
постфиксный бесскобочный формат записи
числового выражения):
>
::
=
|
::
=
+ | − | *
Выражения отделяются друг от друга и от знаков операций ровно одним
пробелом. Создать дерево разбора выражения и вывести указатель на его
корень. Структура дерева разбора выражения описана в задании Tree76;
для каждой вершины-операции ее левое поддерево должно
соответствовать первому операнду данной операции, а правое поддерево
— второму
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
#include #include #include using namespace std; struct Node { char value; Node *left; Node *right; }; Node* create_tree(string s) else // ch - цифра { node->left = NULL; node->right = NULL; }stack[top++] = node; // добавление в стек } } return stack[0]; }; void print_tree(Node* root, int level) { if (!root) return; print_tree(root->left, level + 1); for (int i=0; i level; ++i) cout <" "; cout - >value ; print_tree(root->right, level + 1); }; void print_tree(Node* root) { print_tree(root, 0); } void main() { setlocale(LC_ALL, "Russian"); ifstream* f = new ifstream("input.txt"); string s; //cout //getline (cin, s); getline(*f, s); Node* tree = create_tree(s); //cout print_tree(tree); system("pause"); } описание числового выражения в
следующем формате:
::= |
()
::= + | − | *
Пробелы в строке отсутствуют. Создать дерево, соответствующее
исходному выражению (дерево разбора выражения): каждая внутренняя
вершина дерева должна соответствовать одной из трех возможных
арифметических операций и иметь значение −1 для операции сложения,
−2 для операции вычитания и −3 для операции умножения; левое и
правое дочерние поддеревья любой внутренней вершины-операции
должны соответствовать выражениям слева и справа от знака операции;
листьями полученного дерева должны быть выражения-цифры. Вывести
указатель на корень созданного дерева
Источник
7.5.3. Деревья выражений
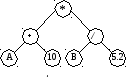
Дерево выражений– бинарное дерево, в корневых узлах которого хранятся признаки операций, а в терминальных узлах – операнды выражения (переменные или константы). Дерево выражений представлено на рис. 73.
Рис. 73. Дерево выражений
Различные алгоритмы обхода дерева выражений соответствуют различной структуре представления выражения в виде строки.
Нисходящему обходу соответствует префиксная формапредставления, т. к. в ней знак операции предшествует операнду:
Восходящему обходу соответствует постфиксная форма представления, т. к. в ней знак операции находится после операндов:
Смешанному обходу соответствует инфиксная форма представления, т. к. в ней знак операции находится между операндами:
Для того чтобы задать приоритеты операций, используется абсолютно скобочная форма, в которой каждое подвыражение заключается в круглые скобки:
( ( A + 10. ) * ( B / 5.2)).
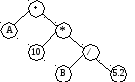
На рис. 74 приведено дерево, смешанный обход которого позволяет получить бесскобочную инфиксную форму, эквивалентную дереву рис. 73, а скобочная инфиксная форма задает совсем другие приоритеты операций. Заметим, что подобная проблема не может возникнуть при использовании префиксной или постфиксной формы представления выражения.
(А + ( 10. * ( В / 5.2 ) ) )
Рис. . Дерево выражений
Какой алгоритм обхода необходимо использовать для того, чтобы подсчитать значение арифметического выражения, представленного в виде дерева?
7.6. Программный модуль, реализующий операции
создания, обработки, просмотра содержимого
бинарного дерева (на примере сбалансированного дерева)
Источник
Помеченные деревья и деревья выражений
Часто бывает полезным сопоставить каждому узлу дерева метку или значение. Дерево, у которого узлам сопоставлены метки, называется помеченным деревом. Метка узла – это значение, которое «хранится» в узле.
Аналогия: дерево – список, узел – позиция, метка – элемент.
Рассмотрим пример дерева с метками, представляющее арифметическое выражение
(a + b)*(a + c), где n1 , n2 , …, n7 – имена узлов, а метки проставлены рядом с соответствующими узлами. Правила соответствия меток деревьев элементам выражений следующие:
Метка каждого листа соответствует операнду и содержит его значение;
Метка каждого внутреннего (родительского) узла соответствует оператору.
Часто при обходе деревьев составляется список не имен узлов, а их меток. В случае дерева выражений при прямом обходе получим префиксную форму записи выражения, где оператор предшествует обоим операндам. В примере получим префиксное выражение вида: *+ ab + ac .
Обратный обход меток дерева дает постфиксное представление выражения (польскую запись). Обратный обход нашего дерева даст нам следующую запись выражения: ab + ac +*.
Префиксная и постфиксная запись выражения не требует скобок.
При симметричном обходе получим обычную инфиксную запись выражения: a + b * a + c . Для инфиксной записи выражений характерно заключение в скобки: ( a + b )*( a + c ).
Реализация деревьев
Пусть дерево T имеет узлы 1, 2, …., n . Cамым простым представлением дерева T будет линейный массив A , где каждый элемент A [ i ] содержит номер родительского узла (является курсором на родителя). Поскольку корень дерева не имеет родителя, то его курсор будет равен 0.
В компьютерных программах деревья обычно описываются в виде динамических структур данных, каждый элемент которых является записью, содержащей информацию о некоторой вершине дерева и набор ссылок на непосредственных потомков данной вершины. Ссылки реализуются в виде указателей, а сами записи размещаются в динамической памяти. В объектно-ориентированных языках программирования со ссылочной объектной моделью вместо записей могут использоваться объекты, содержащие ссылки на другие объекты.
Для приведенного на рисунке дерева построим линейный массив по следующему правилу: A [ i ]= j , если узел j является родителем узла i , A [ i ]=0, если узел i является корнем. Тогда массив будет выглядеть следующим образом:
Другой важный и полезный способ представления деревьев состоит в формировании для каждого узла списка его потомков. Рассмотрим этот способ для приведенного выше примера.
Двоичные деревья
Двоичное или бинарное дерево – это наиболее важный тип деревьев. Каждый узел бинарного дерева имеет не более двух поддеревьев, причем в случае, только одного поддерева следует различать левое или правое. Бинарное дерево – это конечное множество узлов, которое является либо пустым, либо состоит из корня и двух непересекающихся бинарных деревьев, которые называются левым и правым поддеревьями данного корня. Тот факт, что каждый потомок любого узла определен как левый или как правый потомок, существенно отличает двоичное дерево от обычного упорядоченного ориентированного дерева.
Если мы примем соглашение, что на схемах двоичных деревьев левый потомок всегда соединяется с родителем линей, направленной влево и вниз от родителя, а правый потомок – линией, направленной вправо и вниз, тогда деревья, изображенные на рисунке а) и б) ниже, – это различные деревья, хотя они оба похожи на обычное дерево (рис. в)).
Обход двоичных деревьев в прямом и обратном порядке в точности соответствует таким же обходам обычных деревьев. При симметричном обходе двоичного дерева с корнем n левым поддеревом T1 и правым поддеревом T2 сначала проходится поддерево T, затем корень n и далее поддерево T2 .
Источник
20. Помеченные деревья и деревья выражений.
^^Часто бывает полезным сопоставить каждому узлу дерева метку (label) или значение, точно так же, как мы в предыдущей теме сопоставляли элементам списков определенные значения.
^^Дерево, у которого узлам сопоставлены метки, называется помеченным деревом.
^^Метка узла — это не имя узла, а значение, которое «хранится» в узле.
^^В некоторых приложениях требуется изменять значение метки, поскольку имя узла сохраняется постоянным.
^^^^^^^Полезна следующая аналогия: дерево-список, узел-позиция, метка-элемент.
^^Часто при обходе деревьев составляется список не имен узлов, а их меток.
^^В случае дерева выражений при прямом упорядочивании получаем известную префиксную форму выражений, где оператор предшествует и левому, и правому операндам.
^^Для точного описания префиксной формы выражений сначала положим, что префиксным выражением одиночного операнда а является сам этот операнд.
^^Далее, префиксная форма для выражения (E1)q(Е2), где q — бинарный оператор, имеет вид qP1P2, здесь P1, P2 — префиксные формы для выражений E1, Е2.
^^Отметим, что в префиксных формах нет необходимости отделять или выделять отдельные префиксные выражения скобками, так как всегда можно просмотреть префиксное выражение qP1P2 и определить единственным образом P1 как самый короткий префикс выражения P1P2.
^^Например, при прямом упорядочивании узлов (точнее, меток) дерева, показанного на рис., получаем префиксное выражение *+ab+ac. Самым коротким корректным префиксом для выражения +ab+ac будет префиксное выражение узла n2: +ab.
^^При симметричном обходе дерева выражений получим так называемую инфиксную форму выражения, которая совпадает с привычной «стандартной» формой записи выражений, но также не использует скобок. Для дерева на рис. инфиксное выражение запишется как а+b * а+с.
^^Таким образом, требуется разработать алгоритм обхода дерева выражений, который бы выдавал инфиксную форму выражения со всеми необходимыми парами скобок.
21. Абстрактный тип данных «Деревья»
Операторы, выполняемые над деревьями.
Эта функция возвращает родителя (parent) узла n в дереве Т. Если n является корнем, который не имеет родителя, то в этом случае возвращается L («нулевой узел“), что указывает на то, что мы выходим за пределы дерева.
2. LEFTMOST_CHILD(n, Т). Данная функция возвращает самого левого сына узла n в дереве Т. Если n является листом (и поэтому не имеет сына), то возвращается L.
3. RIGHT_SIBLING(n, Т).
Эта функция возвращает правого брата узла n в дереве Т и значение L, если такового не существует. Для этого находится родитель р узла n и все сыновья узла р, затем среди этих сыновей находится узел, расположенный непосредственно справа от узла n.
Возвращает метку узла n дерева Т. Для выполнения этой функции требуется, чтобы на узлах дерева были определены метки.
5. CREATEi(v, Т1, Т2, . Тi)
— это обширное семейство «созидающих» функций, которые для каждого i=0, 1, 2, . создают новый корень r с меткой v и далее для этого корня создает i сыновей, которые становятся корнями поддеревьев Т1, Т2, . Тi.
— Эти функции возвращают дерево с корнем r.
— Для i=0 возвращается один узел r, который одновременно является и корнем, и листом.
— Возвращает узел, являющимся корнем дерева Т. Если Т — пустое дерево, то возвращается L.
— Этот оператор делает дерево Т пустым деревом.
Источник