Дискретная математика дерево корень

2.10. Корневые деревья. Код дерева

Любое дерево можно рассматривать как корневое, если одну из вершин выбрать в качестве корня, а остальные расположить на соответствующих уровнях (ярусах). Пример корневого дерева приведен на рис. 2.26. Корень располагается на нулевом уровне. Припишем каждой вершине некоторое число, называемое весом. Веса концевых вершин равны единице, вес корня дерева равен числу всех его вершин. Вес произвольной вершины равен общему числу вершин поддерева, корнем которого она является. Возле каждой вершины дерева на рис. 2.26 указан ее вес. При таком представлении корневое дерево однозначно определяется упорядоченной последовательностью β( G ) весов его вершин, в которой на первом 40

месте стоит вес корня дерева, а затем следуют соответствующие последова- тельности для поддеревьев: β( G ) = (17, 1, 4, 1, 1, 1, 11, 4, 1, 2, 1, 6, 1, 1, 3, 1, 1).

4	1	1 1	Одна из стандартных проце-
	дур	выбора	корня состоит в сле-
					1	2 1	1
3	дующем: из дерева удаляются все
							1		1	1	3	концевые вершины и ребра, затем
	2	в полученном дереве снова удаля-
4						6
	1	ются все вершины и ребра. В пер-
1
	4	11	вом	случае	оставшаяся	вершина
0							выбирается в качестве корня и
	17		Рис. 2.26		называется						центром, во	втором
случае две вершины и связываю-
щее их ребро образуют бицентр.
При этом за корень принимается та вершина, из которой вырастает дерево

с меньшим числом вершин (если число вершин одинаково, то за корень принимается любая из вершин бицентра).

На рис. 2.27, а приведено дерево,	в котором выделен бицентр, корневая
форма этого дерева изображена на рис. 2.27, б.
корень	3
		бицентр	2
1
	0
а		б

Рис. 2.27 Аналитически корневое дерево можно задать также с помощью кода γ( G ), представляющего собой последовательность 0 и 1, записанную в определенном порядке. Осуществляется обход дерева по всем ребрам по одному разу в каждом из противоположных направлений. При движении по ребру от корневой вершины в последовательность g ( G ) записывается 0, а при обратном движении – 1. Обход начинается и заканчивается в корне дерева. Длина последовательности g ( G ) равна удвоенному количеству ребер дерева. Для графа, приведенного на рис. 2.27, б, g ( G ) = (01001011000110010111). 41

Источник

Тема 3.7 Деревья

Определение: Деревом называется связный, ориентированный граф без петель и кратных ребер, не содержащий в себе циклов, удовлетворяющий следующим условиям:

1. имеется в точности один узел, называемый корнем, в который не входит ни одно ребро,
2. В каждый узел, кроме корня, входит ровно одно ребро,
3. Из корня к каждому узлу идет путь ( который, как легко показать единственный).

Деревья являются простейшим видом связных графов. Любое дерево с n вершинами содержит n-1 ребер. Число различных деревьев, которые можно построить на n вершинах равно Определение Дерево с одной выделенной вершиной называется корневым деревом. Определение Ориентированный граф, состоящий из нескольких деревьев, называется лесом. Определение: Пусть G=(Х, Г) – граф, являющийся лесом. Если дуга (v,w) принадлежит Г, то v называется отцом узла w, а w – сыном узла v. Определение: Если есть путь из v в w, то v называется предком узла w, а w – потомком узла v. Определение: Узел без потомков называется листом. Определение: Узел v и его потомки вместе образуют поддерево леса G, и узел v называется корнем этого поддерева. Определение:Глубина узла v в дереве – это длина пути из корня в v. Определение:Высота узла в дереве – это длина самого длинного пути из этого узла в какой-нибудь лист. Определение:Высотой дерева называется высота его корня. Пример Глубина узла b, в данном примере, = 1, а его высота = 2. Высота дерева = 3. Определение:Упорядоченным деревом называется дерево, в котором множество сыновей каждого узла упорядоченно. При изображении упорядоченного дерева, как правило, считается, что множество сыновей каждого узла упорядоченно слева направо. Определение:Бинарным деревом называется такое упорядоченное дерево, что

1. Каждый сын произвольного узла идентифицируется либо как левый сын, либо как правый сын.
2. Каждый узел имеет не более одного левого и не более одного правого сына.

Обратите внимание, что бинарное дерево не является частным случаем дерева, это совершенно иное, хотя и тесно связанное понятие. Например: Указанные бинарные деревья различны между собой ( в первом случае корень имеет пустое правое поддерево, а во втором левое поддерево пусто), хотя как деревья они изоморфны, и мы можем рассматривать их как одно дерево. Определение: Бинарное дерево называется полным, если для некоторого целого числа K каждый узел, глубины меньшей k имеет как левого, так и правого сына, и каждый узел глубины k является листом. Полное дерево глубины k имеет узлов. Очень часто используются алгоритмы, которые проходят дерево (посещают каждый его узел) в некотором порядке. Известно несколько способов сделать это. Мы рассмотрим три широко известных способа: прохождение дерева в прямом порядке, обратном порядке и внутреннем. Будем считать, что Т – дерево с корнем r и сыновьями при k >=0. При k = 0 это дерево состоит из единственного узла r.

Прохождение дерева т в прямом порядке определяется следующим алгоритмом:

1. Посетить корень r
2. Посетить слева на право поддеревья с корнями v1 . . . vk в указанной последовательности.

П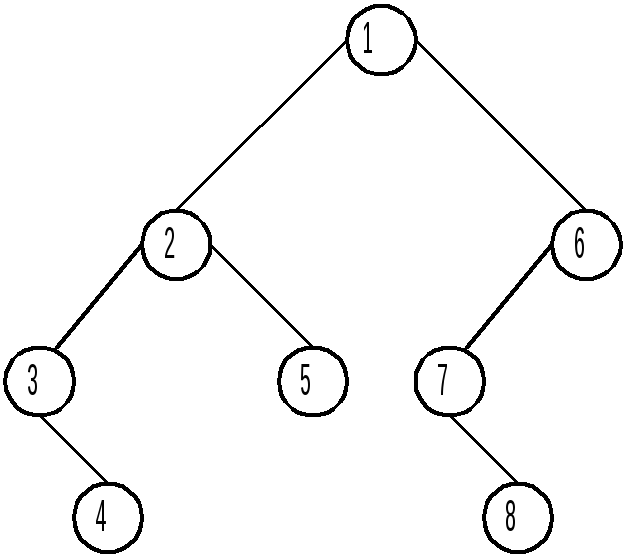ример Прохождение дерева Т в обратном порядке определяется следующим алгоритмом: Посетить в обратном порядке поддеревья с корнями v1 . . . vk в указанной последовательности. Посетить корень r Пример Прохождение дерева Т во внутреннем порядке определяется следующим алгоритмом: Посетить во внутреннем порядке левое поддерево корня (если оно существует). Посетить корень Посетить во внутреннем порядке правое поддерево корня (если оно существует). Пример Прежде чем дать описание одного из этих алгоритмов на некотором формальном языке программирования, поговорим о способах задания и хранения деревьев и бинарных деревьев. Очень многие объекты представимы в виде деревьев. Например: сложная нумерация глав лекций – типичный информационный объект, сохраняемый и обрабатываемый в виде дерева. 1. Теория графов 1.1. Основные определения теории графа 1.2. Операции над графами 1.2.1. Одноместные операции 1.2.2. Двуместные операции 1.3. Отношения 1.3.1. Отношение порядка 1.3.2. Отношение эквивалентности

1. Числовые характеристики графа

1.5. Понятие обхода графа 1.5.1. Эйлеров цикл 1.5.2. Гамильтонов цикл

1. Изоморфизм графов
2. Понятие дерева
3. Бинарные деревья
4. Алгоритмы нумерации узлов графа
   1. Нумерация в прямом порядке
   2. Нумерация в обратном порядке
   3. Нумерация во внутреннем порядке

Подобная система нумерации часто называется десятичной системой обозначения Дьюи. Введем интуитивное понятие линейного списка. Мы еще не раз будем говорить об этом способе представления и хранения информации. Одним из распространенных способов хранения деревьев является массив списков. Это одномерный массив, размерностиn – количество узлов дерева. Каждый элемент этого массива – это упорядоченный или неупорядоченный список сыновей этого отца. Например Бинарные деревья, как правило, хранятся посредством двух массивов ЛЕВЫЙСЫН и ПРАВЫЙСЫН, где номер элемента массива – это номер узла, а значение этого элемента – номер левого или правого узла – сына. Если элемент — сын отсутствует, то значение равно 0. Пример Теперь опишем алгоритм нумерации узлов двоичного дерева в соответствии с внутренним порядком. Для этого будем пользоваться неким подобием языка программирования, специально предназначенного для прозрачного и понятного описания алгоритмов. Вход: Двоичное дерево, представленное массивами ЛЕВЫЙСЫН и ПРАВЫЙСЫН. Выход: Массив, называемый НОМЕР, такой, что НОМЕР[i] – номер i – того узла во внутреннем порядке. Метод: Будем использовать глобальную переменную СЧЕТ, значение которой – номер очередного узла в соответствии с внутренним порядком. Начальное значение переменной СЧЕТ = 1. Программа выглядит так: begin СЧЕТ  1 ВНУТРПОРЯДОК(КОРЕНЬ) EndProcedure ВНУТРПОРЯДОК(УЗЕЛ) Begin 1. if ЛЕВЫЙСЫН[УЗЕЛ]0 then ВНУТРПОРЯДОК(ЛЕВЫЙСЫН[УЗЕЛ]); 2. НОМЕР[УЗЕЛ]  СЧЕТ;

1. СЧЕТ  СЧЕТ+1

4. if ПРАВЫЙСЫН[УЗЕЛ]0 then ВНУТРПОРЯДОК(ПРАВЫЙСЫН[УЗЕЛ]); End Такая процедура, которая явно или неявно вызывает сама себя, называется рекурсивной. Применение рекурсии часто дает возможность давать более прозрачное и сжатое описание алгоритма, чем это же можно было бы сделать, не используя рекурсию. Если бы приведенный алгоритм не был записан рекурсивно, надо было бы строить явный механизм для прохождения дерева. Двигаться вниз по дереву нетрудно, но чтобы обеспечить возможность вернуться к предку, надо запомнить всех предков в стеке, а операторы работы со стеком усложнили бы алгоритм, лишив его наглядности.

Источник

3.10. Кодирование деревьев

Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называетсякорневым.

Для задания (с точностью до изоморфизма) корневыхдеревьев используюткод из 0 и 1, который мы определим индуктивно.

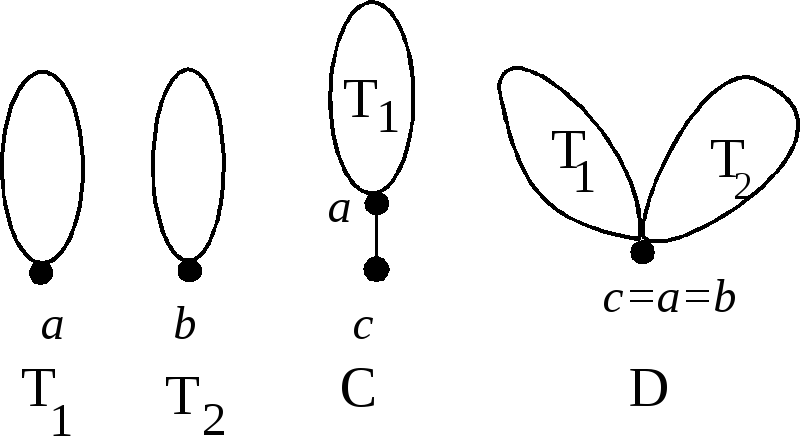
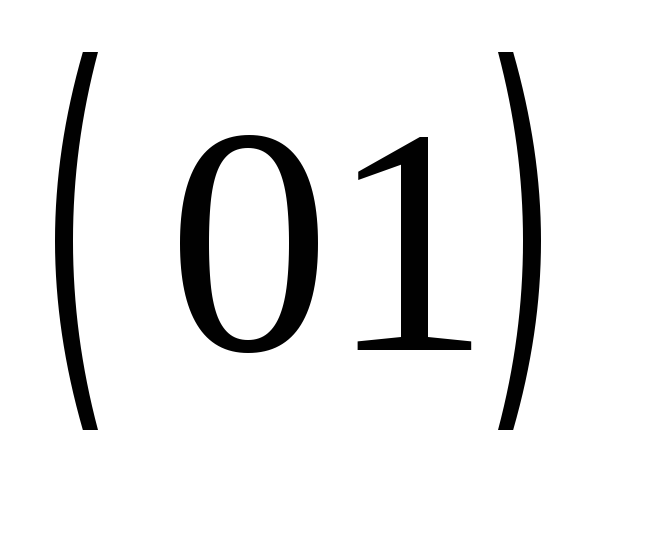
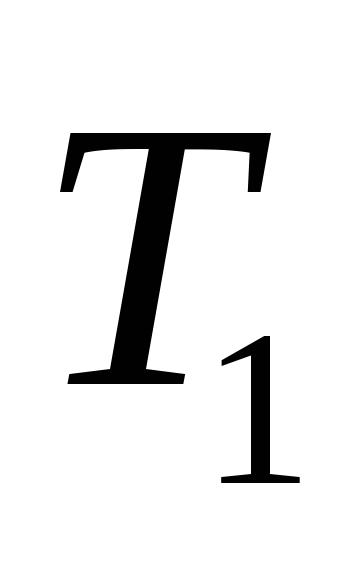
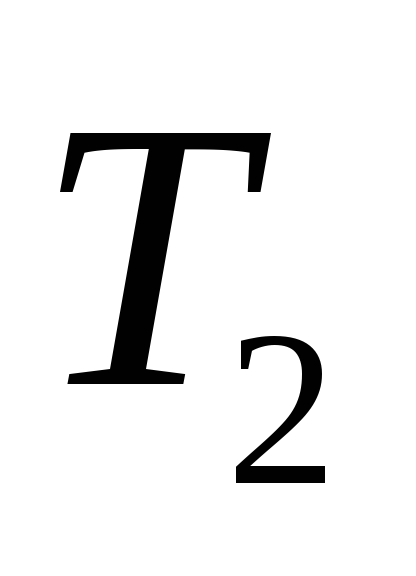
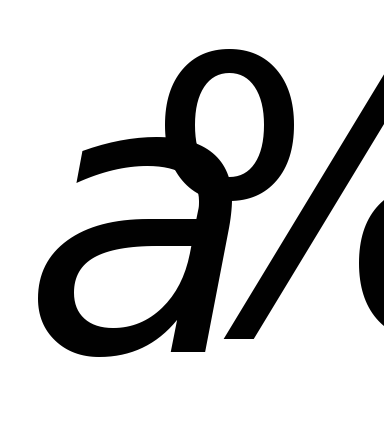
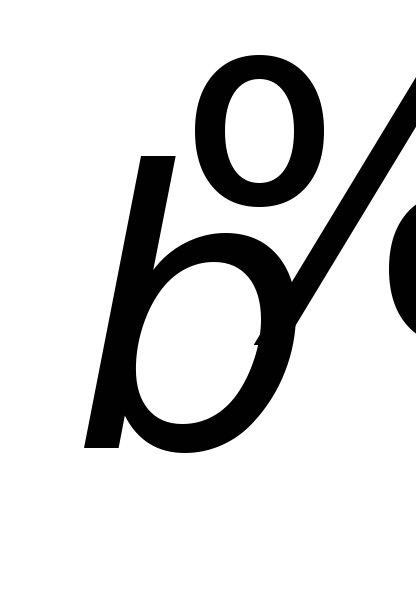
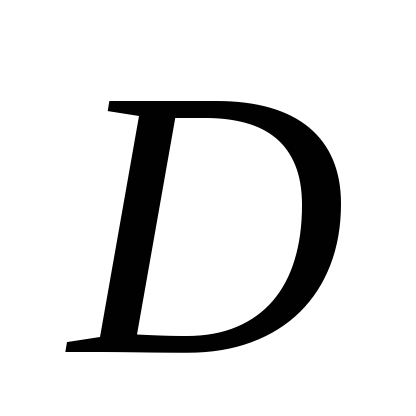
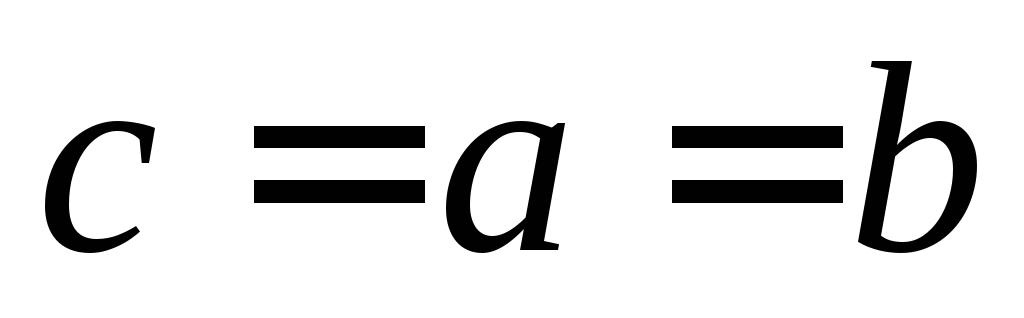
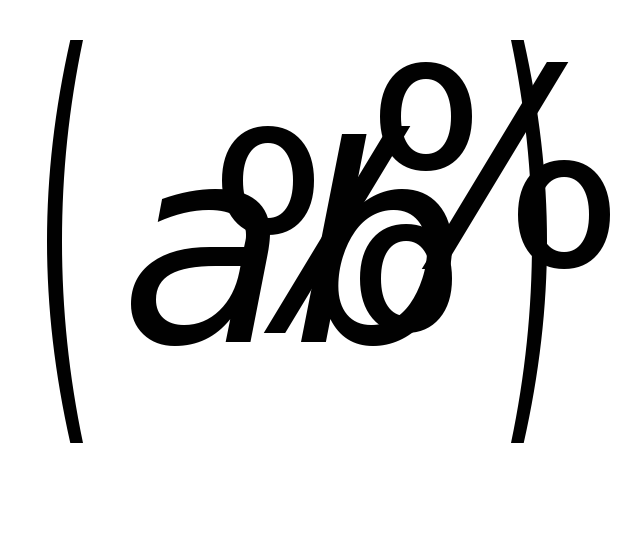
Определение.Кодом корневого дерева с одним ребром является .Пусть деревья и с корнямиa и b соответственно (см. рис.) имеют коды и .Тогда кодом дерева с корнем с является код , а кодом дерева с корнем — код.

Пример 1. Написать код дерева, изображенного на рисунке.

И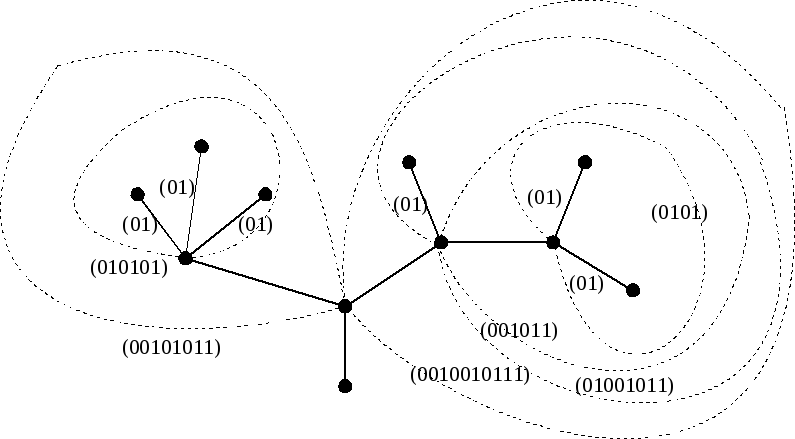так, код дерева —.

Справедливо следующее утверждение:для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева необходимо и достаточно, чтобы число нулей и единиц в этой последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.

Чтобы построить корневое дерево по кодуиз нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшаяся в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками, то каждая такая скобка будет соответствовать ребру графа.

П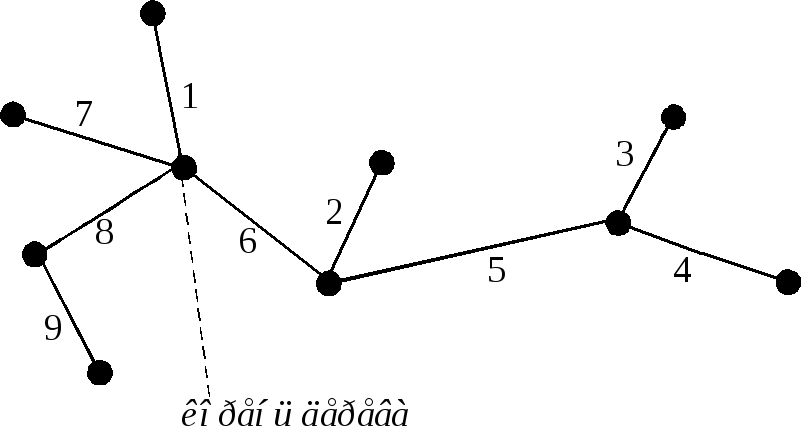ример 2.Построить дерево по коду.

Для задания помеченныхдеревьев, т.е. деревьев, вершины которых занумерованы, используют код из натуральных чисел.

Пусть дано помеченное дерево. Чтобы построить его код из натуральных чисел действуем следующим образом. Находим висячую вершину с наименьшим номером. Записываем номер смежной с ней вершины (это начало кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находим висячую вершину с наименьшим номером, записываем номер смежной с ней вершины (это продолжение кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Так поступаем до тех пор, пока не останется последнее ребро.

Заметим, что длина кода из натуральных чисел на единицу меньше числа ребер и на две единицы меньше числа вершин данного дерева.

Пример 3.На рисунке изображено помеченное дерево. Его код.

Построение дерева по коду из натуральных чиселрассмотрим на примере кода. Прежде всего, заметим, что дерево, которое нам предстоит построить, имеет 8 вершин.

Источник

3.05.2. Корневое дерево

Корневое дерево Есть специальный способ представления (изображения) дерева. Выбирается некоторая вершина, которая именуется «корнем дерева». При изображении все вершины располагают по ярусам, следующим образом. На нулевом ярусе располагается корень дерева (см. рис.). на 1 ярусе располагают все вершины дерева, смежные с корнем; затем на 2 ярусе — все вершины, смежные с вершинами 1-го яруса; на 3-ем — вершины, смежные с с вершинами 2-го яруса и так далее.

Каждому корневому дереву ставится в соответствие его бинарный Код, который строится в процессе полного обхода дерева. Обход начинается с корня и заканчивается корнем. Обход осуществляется слева направо, т. е. сначала проходится левая ветвь, затем следующая и так далее, в конце — самая правая. При обходе необходимо подниматься по ветви (см. следующий рис.) до тех пор, пока это возможно. Затем по ветви опускаются до тех пор, пока не появится возможность продолжить подъем по еще не пройденной ветви. При подъеме с одного яруса на следующий в код дерева записывается 1, при опускании с яруса на ярус — 0. Так дерево на рисунке имеет код (11101101000011011011000100).

Легко видеть, что код дерева обладает следующими свойствами:

· длина кода дерева порядка 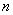Равна ;

· число нулей равно числу единиц;

· если обрубить код на каком-либо месте, то число единиц на участке от начала кода до данного места не меньше числа нулей на этом участке (разность между этим количеством совпадает с ярусом, на котором прерван обход).

Обратно, по всякому бинарному набору, обладающему этими свойствами, можно построить корневое дерево, код которого совпадает с данным набором.

Источник