Дискретная математика деревья решение

Примеры решения задач

Задача 1. Восстановить и нарисовать бинарное ордерево по префиксному коду .

Решение. Наибольшая длина двоичной строки равна трем, следовательно, глубина ордерева также равна трем. Так как в префиксном коде указаны только висячие вершины, то по ним и восстанавливаем ордерево

Задача 2. Построить код Прюфера для дерева

123456789

– код Прюфера

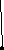
Задача 3. Восстановить дерево по коду Прюфера

Решение. Число символов в коде n-2=6, значит, у дерева n=8 вершин. Наименьшим из номеров, не входящих в код, является 3, значит, вершина 3 инцидентна вершине 1. Вычеркиваем 3 из списка вершин и просматриваем список дальше. Наименьшим из оставшихся и не входящих в код номеров является 5. Вершина 5 инцидентна вершине 1.

1 2 3 4 5 6 7 8 31.

1 2 3 4 5 6 7 8 51.

1 2 3 4 5 6 7 8 74

(вершина 4 становится висячей).

1 2 3 4 5 6 7 8 41

(вершина 1 становится висячей).

1 2 3 4 5 6 7 8 16

(вершина 6 становится висячей).

1 2 3 4 5 6 7 8 62.

Задачи для самостоятельного решения

Задача 2. Написать код Прюфера для данного дерева:

§8. Обход дерева. Понятие списка. Деревья и списки

Часто необходимо обойти все вершины большого дерева не хаотически, а по определенному алгоритму. Для бинарных ориентированных деревьев существует три канонических способа обхода.

1. Прямой (КЛП – корень, лево, право). Сначала мы учитываем корень, затем левое поддерево и правое поддерево. Это правило выполняется для каждой вершины, начиная с корня.
2. Обратный (ЛКП – лево, корень, право). Сначала мы учитываем левое поддерево, затем корень и правое поддерево. Это правило выполняется для всех вершин, начиная с корня.
3. Концевой (ЛПК – лево, право, корень). Сначала мы учитываем левое поддерево, затем правое и корень.

Примеры решения задач

Задача 1. Обойти тремя способами бинарное дерево 1 3 2 7 4 6 5 11 8 9 10 Решение. 1. Прямой (КЛП). 1 2 4 5 8 3 6 9 7 10 11. 2. Обратный (ЛКП) 4 2 8 5 1 6 9 3 1 0 7 1 1. 3. Концевой (ЛКП) 4 8 5 2 9 6 1 0 1 1 7 3 1. Задача 2. Нарисовать дерево, соответствующее списку: а) (а); б) (а,b,с); в) (а,(b,с), (е,(f,k))). Решение. а) б) с) а b k е с а f

Источник