Длина самого длинного пути от корня дерева до листа

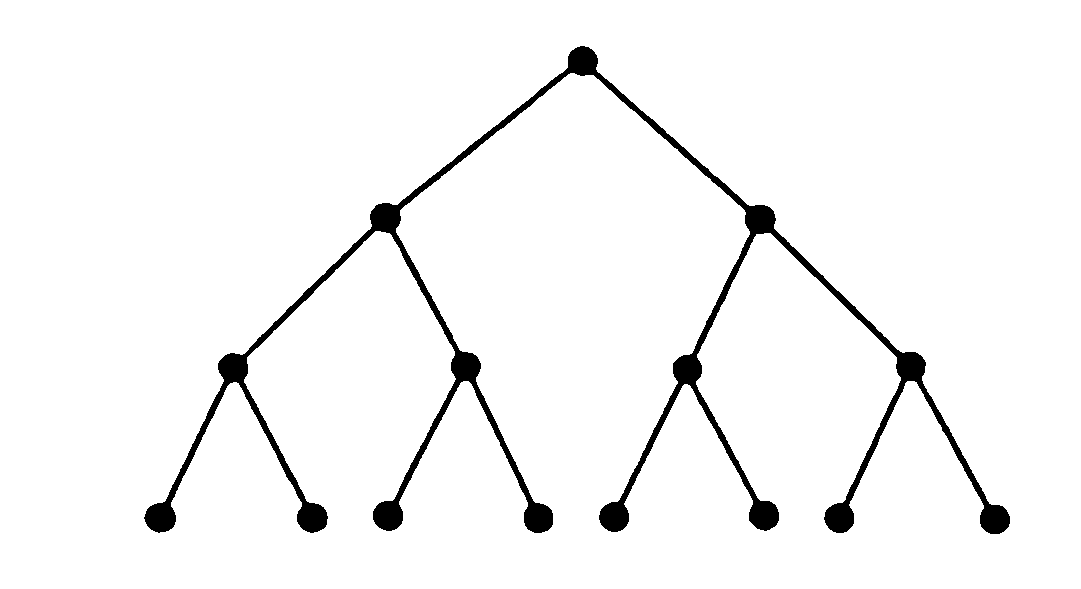
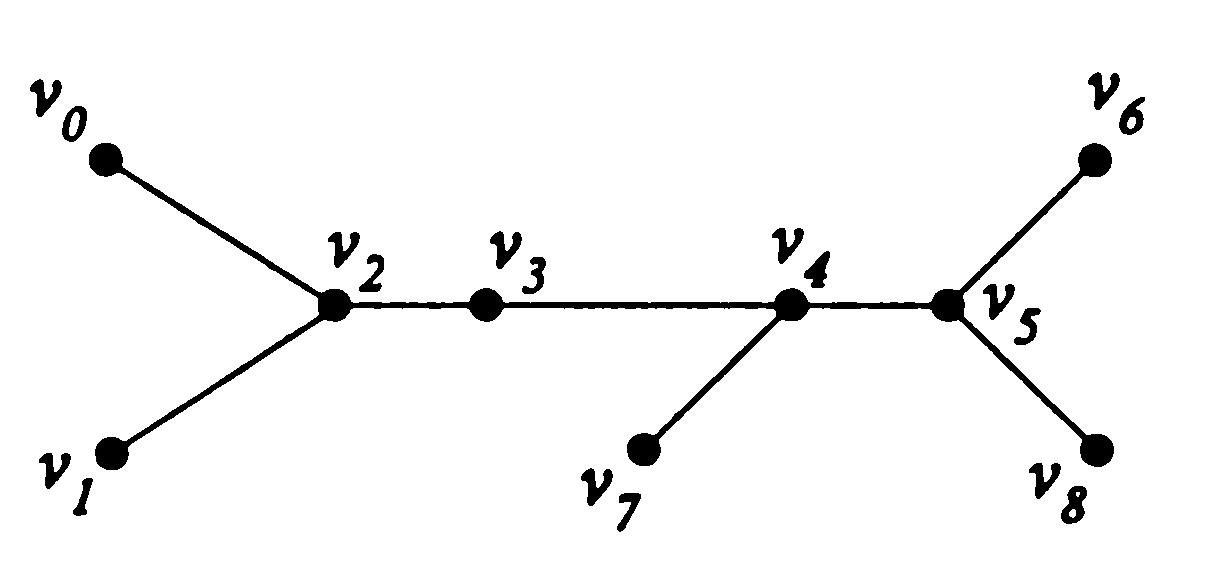
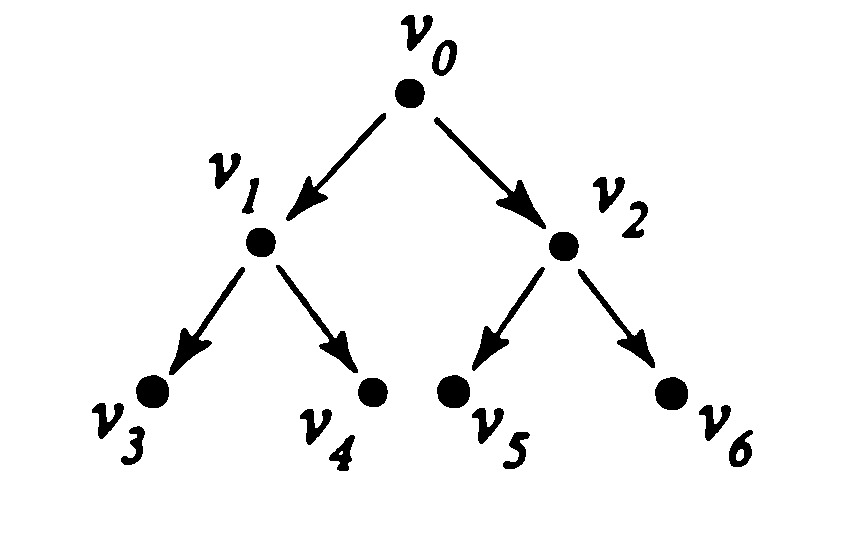
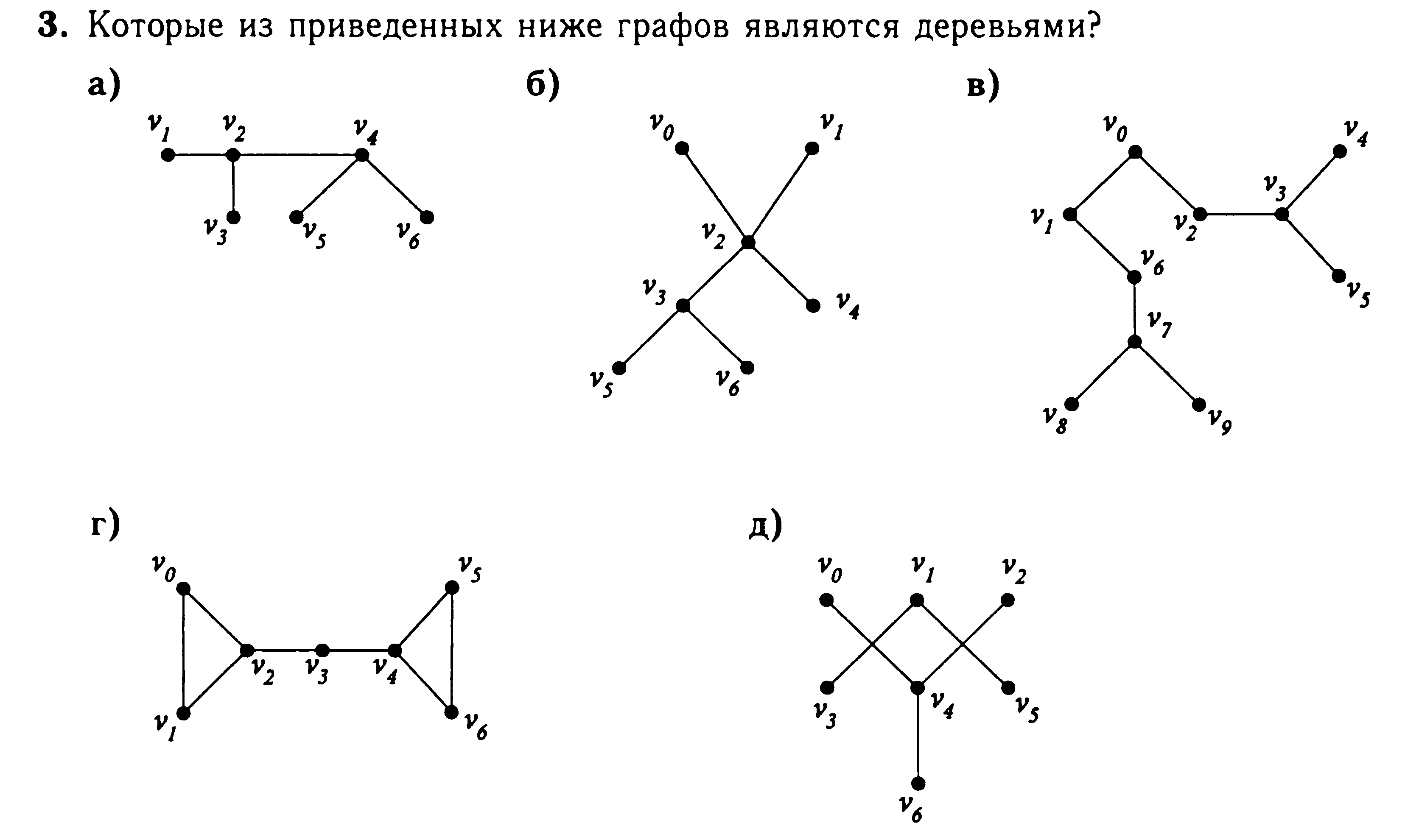
Найти глубину дерева, представляемую как наибольшая длина пути от корня к листьям.

В общем дано двоичное дерево надо была найти глубину дерева, представляемую как наибольшая длина пути от корня к листьям. Правильно ли прога это делает?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130

uses crt; type PNode = ^Node; Node = record data: integer; left, right: PNode; end; var Tree, p1: PNode; n, x, i, max: integer; ch: char;  procedure AddToTree(var Tree: PNode; x: integer); begin if Tree = nil then begin New(Tree); Tree^.data := x; Tree^.left := nil; Tree^.right := nil; exit; end; if x < Tree^.data then AddToTree(Tree^.left, x) else AddToTree(Tree^.right, x); end; procedure node_length(var Tree: PNode); var l, r: PNode; begin if (Tree^.left <> nil) and (Tree^.right <> nil) then begin l := Tree^.left; r := Tree^.right; node_length(l); node_length(r); writeln(max); inc(max); end; if (Tree^.left <> nil) and (Tree^.right <> nil) then max := max - 1; if (Tree^.left <> nil) or (Tree^.right <> nil) then max := max + 1; end; function Search(Tree: PNode): PNode; var p: PNode; begin if (Tree^.left <> nil) and (Tree^.right <> nil) then begin if Tree^.left = nil then p := Search(Tree^.right); if Tree^.right = nil then p := Search(Tree^.left); p := Search(Tree^.right); p := Search(Tree^.left); end; Search := p; end; procedure Lkp(Tree: PNode); begin if Tree = nil then exit; Lkp(Tree^.left); write(' ', Tree^.data); Lkp(Tree^.right); end; procedure DeleteTree(var Tree1: PNode ); begin if Tree1 <> nil then begin DeleteTree(Tree1^.LEFT); DeleteTree(Tree1^.RIGHT); Dispose(Tree1); end; end; begin Tree := nil; repeat Writeln('Выберете действие '); Textcolor(3); Writeln('______________________'); Writeln('1) Создание дерева '); Writeln('2) Глубина дерева'); Writeln('3) Вывод дерева'); Writeln('4) Выход'); writeln; readln(ch); case ch of '1': begin writeln(' Введите количество элементов дерева :'); readln(n); for i := 1 to n do begin writeln('Введите элемент'); readln(x); clrscr; AddToTree(Tree, x); end; end; '2': begin max := 1; node_length(Tree); writeln('Глубина дерева ', max); end; '3': begin writeln(' Дерево'); Lkp(Tree); writeln; end; end; until ch = '4'; DeleteTree(Tree); end.

Источник

3.2.3. Терминология деревьев

В предыдущих разделах уже были введены основные термины, касающиеся деревьев. Учитывая важность темы, рассмотрим этот вопрос подробно.

Стандартная терминология деревьев происходит от генеалогических деревьев. Каждый узел (элемент дерева) является родителем (parent) корней его поддеревьев, а сами корни называются братьями, а также детьми (child) или сыновьями своего родителя. Узлы, которые или являются детьми данного узла, или являются детьми его детей, называются потомками данного узла. И наоборот, родитель узла, а также родители родителей называются предками узла. Корень является общим предком всех узлов дерева. Сыновья узла иногда называются его непосредственными (истинными) потомками, а родитель — истинным предком.

Узел, не имеющий детей, называется листом или внешним узлом (leaf, external node). Остальные узлы являются внутренними (internal). Количество детей (непосредственных потомков) узла называется его степенью. Листья имеют степень ноль. Если максимальная степень узлов дерева больше двух, то такие деревья называют сильно ветвящимися.

Основное свойство корневых деревьев — путь от корня до любого узла всегда существует и является единственным. Это свойство вытекает из того факта, что в иерархических структурах каждый узел всегда имеет только одного родителя (одну линию связи с родительским узлом), а значит, и единственный путь до корня дерева.

Высотой (height) узла дерева называется длина самого длинного пути из этого узла до какого-либо листа. Высота дерева совпадает с высотой корня.

Уровень узла (level) определяется как длина пути от корня до этого узла. Корень имеет уровень ноль. Все братья имеют один и тот же уровень, который на единицу больше уровня их отца. Например, на рис. 3.2 братья a, b и c имеют уровень 1, а сыновья узла с (братья e,f и g) имеют уровень 2. Высота дерева на рис.3.2 равна трем.

3.2.4. Упорядоченные деревья и леса. Связь с иерархическими списками

Упорядоченное (ordered) дерево — дерево, у которого относительный порядок сыновей (поддеревьев) имеет значение. Обычно сыновья упорядочиваются слева направо. Поэтому два дерева на рисунке 3.4. различны, так как порядок сыновей узла а различен.

Рис. 3.4. Два различных упорядоченных дерева

Если порядок сыновей игнорируется, то такое дерево называется неупорядоченным. В большинстве алгоритмов используются упорядоченные деревья, очевидно, это объясняется тем, что расположение данных в памяти компьютера всегда имеет определенный порядок.

Если дерево является упорядоченным, то и каждый лес, являющийся частью этого дерева, также является упорядоченным. Упорядоченный лес можно рассматривать как линейный список деревьев, в котором можно четко выделить первое дерево (оно расположено слева от всех своих братьев), второе и т. д. Аналогично списку, в частном случае упорядоченный лес может не содержать ни одного дерева (быть пустым) или содержать одно единственное дерево.

Такое представление упорядоченного леса позволяет рассматривать упорядоченные леса (и деревья) как одну из разновидностей иерархических списков (вспомним определение иерархического списка). Однако иерархические списки считаются более универсальной структурой данных [8]:

несколько иерархических списков может пересекаться (т. е. иметь одинаковые подсписки);

иерархические списки могут даже быть рекурсивными (т. е. содержать ссылки на самих себя).

Такие возможности не противоречат определению иерархического списка, но не допустимы для деревьев исходя из их определения. Другими словами, для каждого дерева существует эквивалентная структура иерархического списка, однако есть иерархические списки, которые не соответствуют никакой древовидной структуре.

Строго говоря, иерархические списки, которые пересекаются или содержат ссылку на самих себя, уже нельзя отнести к иерархическим структурам данных, правильнее назвать их многосвязными структурами. В фундаментальной работе [8] они рассматриваются именно как многосвязные структуры и называются Списками (с заглавной буквы). В реальных задачах такие нетривиальные случаи встречаются редко, поэтому термин «иерархические списки» — достаточно устоявшееся название подобных структур данных.

Далее рассмотрим еще один вид деревьев — бинарные.

Источник

8. Остовы и деревья

Понятие дерева широко используется во многих областях математики и информатики. Например, как инструмент при вычислениях, как удобный способ хранения данных, способ сортировки или поиска данных.

Достаточно развитое генеалогическое дерево образует дерево.

Типичное частичное организационное дерево для университета.

Если дерево имеет хотя бы одно ребро, оно имеет две вершины со степенью 1. Вершины со степенью 1 называются листьями. Другие вершины называются внутренними вершинами.

Предположим, что дерево представляет физический объект, подвижный в вершинах, и подвесим дерево за одну из его вершин:

Если подвесить за вершину V3 или V4

Вершина в верхней части называется корнем дерева, если корень определен, то дерево называется корневым. При необходимости корневое дерево Т можно заменить на ориентированное корневое дерево Т’, порожденное корневым деревом Т.

Если корень выбран, уровень вершины V определяется длиной единственного пути из корня в вершину V. Высотой дерева называется длина самого длинного пути от корня дерева до листа.

Если рассматривается корневое ориентированное дерево Т’, порожденное данным корневым деревом Т, тогда вершина u называется родителем вершины v; a v называется сыном вершины u, если существует ориентированное ребро из u в v.

Если u — родитель v и v1, тогда v и v1 называются братьями.

Если существует ориентированный путь из вершины u в вершину v, тогда u называется предком вершины v, a v называется потомком вершины u.

Если наибольшая из степеней выхода для вершин дерева равна m, тогда дерево называется m — арным деревом.

В частном случае, когда m = 2, дерево называется бинарным деревом.

В каждом бинарном дереве каждый сын родителя обозначается либо как левый сын, либо как правый сын (но не то и другое одновременно).

Связный граф G(V,E), не имеющий циклов, называется деревом.

ТЕОРЕМА (основные свойства деревьев):

Пусть граф G(V,E) имеет n вершин. Тогда следующие утверждения эквивалентны:

1. G является деревом;
2. G не содержит циклов и имеет n-1 рёбер;
3. G связен и имеет n-1 рёбер;
4. G связен, но удаление » ребра нарушает связность;
5. » две вершины графа G соединены ровно одним путём;
6. G не имеет циклов, но добавление » ребра порождает ровно один цикл.

Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины (за исключением одной, например v₁) не больше 1, а полустепень захода вершины v₁ (называемой также корнем) равна нулю. Вершину v ордерева называют потомком вершины u, если $ путь из u в v. В этом же случае вершину u называют предком вершины v. Вершину, не имеющую потомков, называют листом. 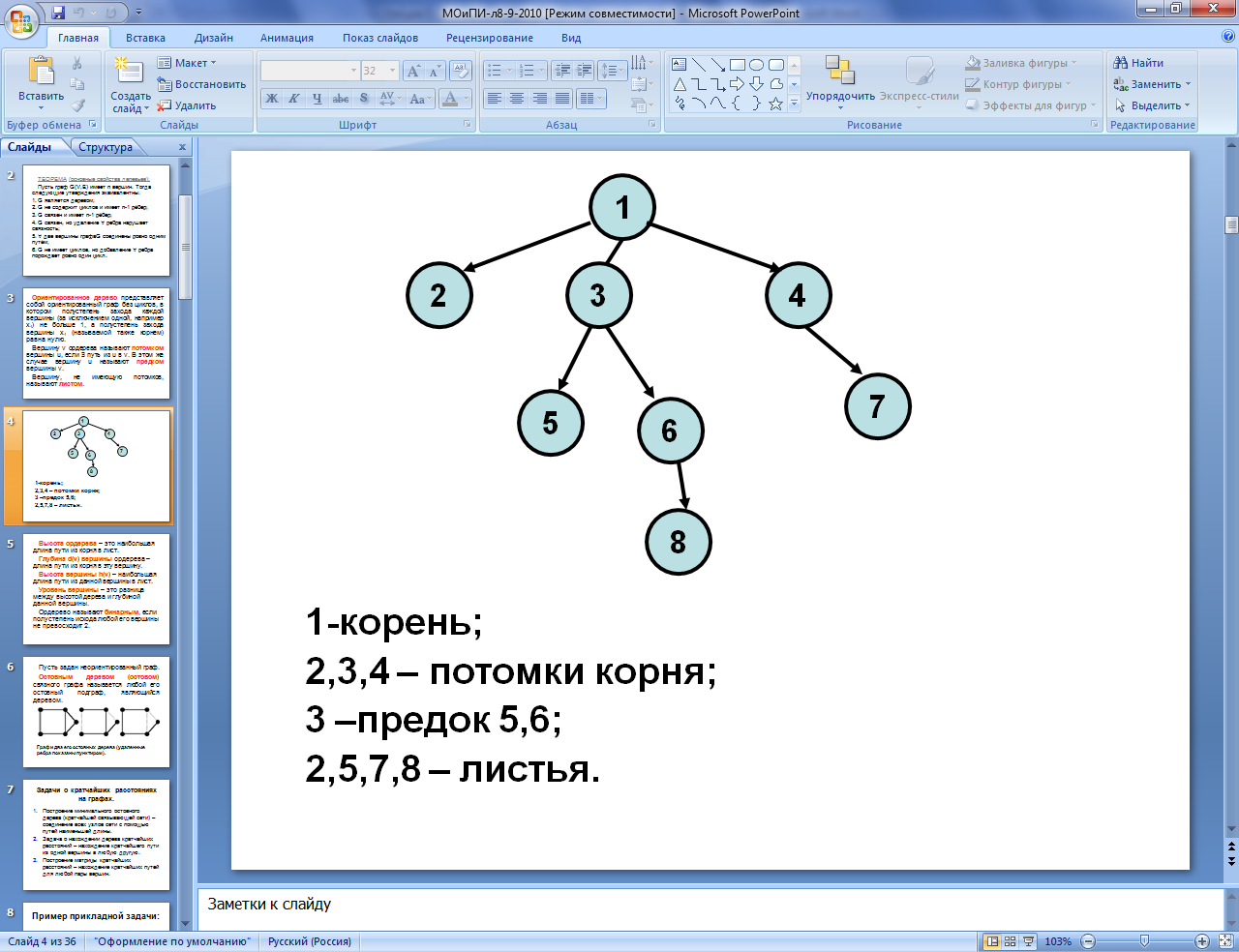Высота ордерева – это наибольшая длина пути из корня в лист. Уровень вершины ордерева – длина пути из корня в эту вершину. Ордерево называют бинарным, если полустепень исхода любой его вершины не превосходит 2. Пусть задан неориентированный граф. Остовным деревом (остовом) связного графа называется любой его остовный подграф, являющийся деревом. Граф и два его остовных дерева (удаленные ребра показаны пунктиром).Задачи о кратчайших расстояниях на графах.

1. Построение минимального остовного дерева (кратчайшей связывающей сети) – соединение всех узлов сети с помощью путей наименьшей длины.
2. Задача о нахождении дерева кратчайших расстояний – нахождение кратчайшего пути из одной вершины в любую другую.
3. Построение матрицы кратчайших расстояний – нахождение кратчайших путей для любой пары вершин.

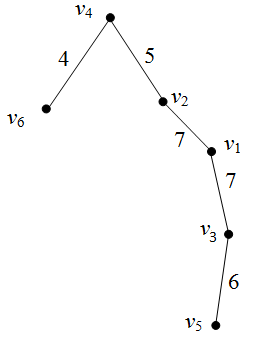
Необходимо проложить линии коммуникаций (дороги, линии связи, электропередач и т.п.) между n заданными «точечными» объектами, при условии: во-первых, известны «расстояния» между каждой парой объектов (это может быть геометрическое расстояние или стоимость прокладки коммуникаций между ними), во-вторых, объекты могут быть связаны как непосредственно, так и с участием произвольного количества промежуточных объектов. При допущении, что разветвления возможны только в этих же n объектах, задача сводится к нахождению кратчайшего остовного дерева (SST — shortest spanning tree, или MST — minimal spanning tree) во взвешенном графе, вершины которого соответствуют заданным объектам, а веса ребер равны «расстояниям» между ними. Определение.Весостовного дерева взвешенного графа G равен сумме весов, приписанных ребрам остовного дерева. Будем обозначать (T). Минимальным остовным деревом (МОД) называется такое остовное дерево графа G, что вес T меньше или равен весу любого другого остовного дерева графа G. Вес минимального остовного дерева будем обозначать _min(T). Задача 1:найти кратчайшее остовное дерево (минимальный покрывающий остов) взвешенного графа. Пусть дан неориентированный связный граф со взвешенными ребрами. Вес ребра (x_i,x_j) обозначим c_ij. Из всех остовов графа необходимо найти один, у которого сумма весов на ребрах наименьшая. Стоимость остовного дерева вычисляется как сумма стоимостей всех рёбер, входящих в это дерево. 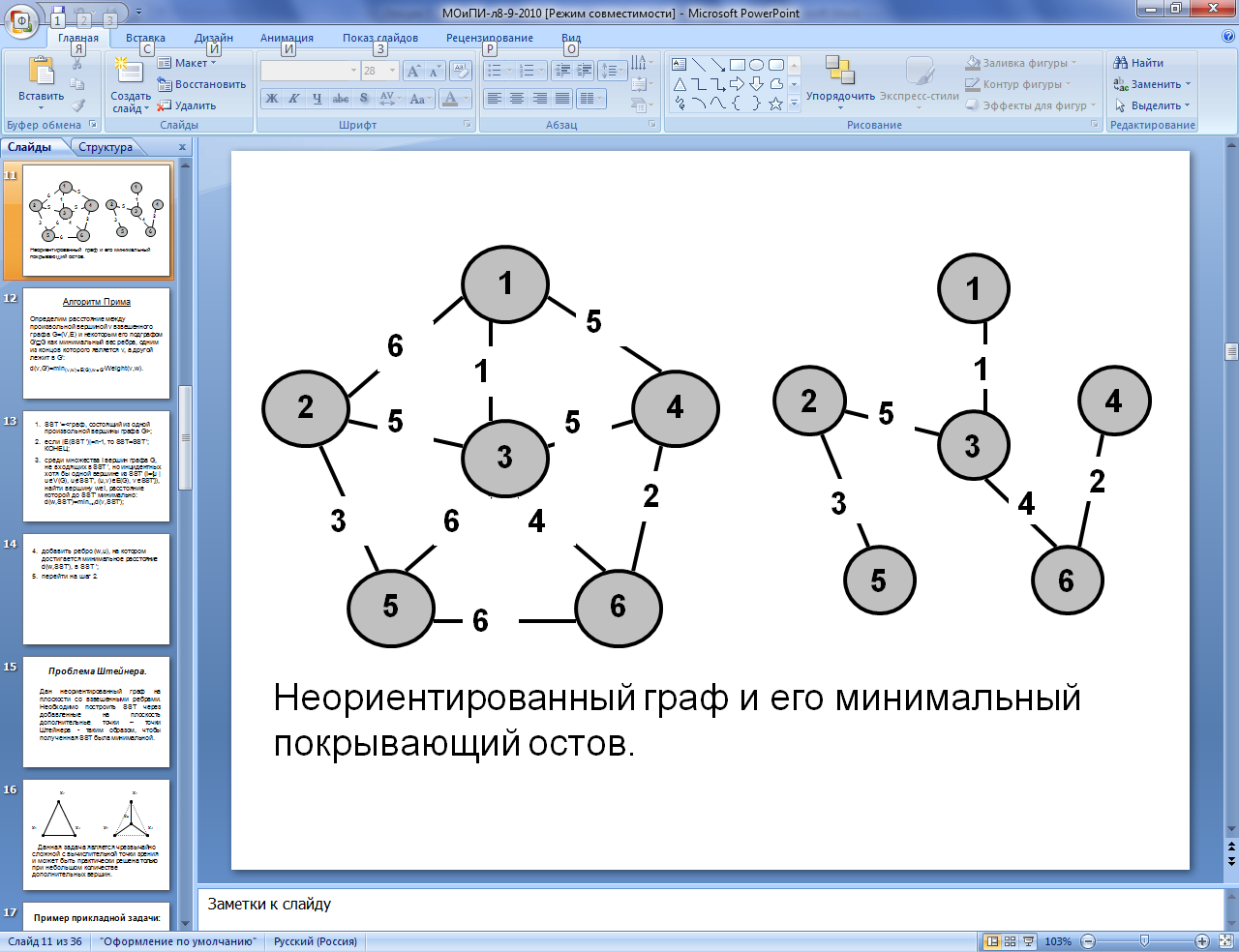Построение остова графа G, имеющего наименьший вес, имеет широкое применение при решении некоторого класса задач прикладного характера. Например: Пусть, например, G=(V, E, ) служит моделью железнодорожной сети, соединяющей пункты v₁, v₂, …, v_nV, а (v_i, v_j) – расстояние между пунктами v_i и v_j. Требуется проложить сеть телеграфных линий вдоль железнодорожной сети так, чтобы все пункты v₁, v₂, …, v_n были связаны между собой телеграфной сетью, протяженность которой была бы наименьшей. Рассмотрим два способа построения минимального остовного дерева взвешенного графа: алгоритм Крускала и алгоритм Прима. Алгоритм Крускала: 1) Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T. 2) Добавить это ребро во множество ребер E. 3) Продолжить, пока имеются ребра, обладающие указанными свойствами. Пример. Для данного взвешенного графа найти минимальное корневое остовное дерево, используя алгоритм Крускала. Определить высоту построенного дерева. Алгоритм Крускала. Выбираем ребро с минимальным весом. Это ребро, (, ) с весом, равным 4. Пусть вершина будет корнем дерева. Далее выбираем ребра, инцидентные вершинам , и имеющие минимальный вес. Это ребро (, ) с весом 5. Затем к вершине присоединяем ребро (,) с весом 7. Далее, добавляем ребро (, ) с весом 7 и ребро (,) с весом 6. Минимальный вес построенного дерева равен: _min(T)=4+5+7+7+6=29.

Источник