Динамические структуры данных: бинарные деревья
Аннотация: В лекции рассматриваются определения, свойства и виды деревьев, элементы, характеристики и способы объявления деревьев в программах, основные операции над элементами деревьев, понятие и виды обходов деревьев, приводятся примеры реализации основных операций над бинарными деревьями в виде рекурсивных функций.
Цель лекции: изучить понятие, формирование, особенности доступа к данным и работы с памятью в бинарных деревьях, научиться решать задачи с использованием рекурсивных функций и алгоритмов обхода бинарных деревьев в языке C++.
Дерево является одним из важнейших и интересных частных случаев графа. Древовидная модель оказывается довольно эффективной для представления динамических данных с целью быстрого поиска информации .
Деревья являются одними из наиболее широко распространенных структур данных в информатике и программировании, которые представляют собой иерархические структуры в виде набора связанных узлов.
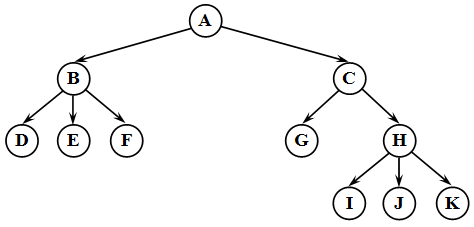
Дерево – это структура данных , представляющая собой совокупность элементов и отношений, образующих иерархическую структуру этих элементов ( рис. 31.1). Каждый элемент дерева называется вершиной (узлом) дерева. Вершины дерева соединены направленными дугами, которые называют ветвями дерева. Начальный узел дерева называют корнем дерева, ему соответствует нулевой уровень. Листьями дерева называют вершины, в которые входит одна ветвь и не выходит ни одной ветви.
Каждое дерево обладает следующими свойствами:
- существует узел, в который не входит ни одной дуги (корень);
- в каждую вершину, кроме корня, входит одна дуга.
Деревья особенно часто используют на практике при изображении различных иерархий. Например, популярны генеалогические деревья.
Все вершины, в которые входят ветви, исходящие из одной общей вершины, называются потомками, а сама вершина – предком. Для каждого предка может быть выделено несколько. Уровень потомка на единицу превосходит уровень его предка. Корень дерева не имеет предка, а листья дерева не имеют потомков.
Высота (глубина) дерева определяется количеством уровней, на которых располагаются его вершины. Высота пустого дерева равна нулю, высота дерева из одного корня – единице. На первом уровне дерева может быть только одна вершина – корень дерева , на втором – потомки корня дерева, на третьем – потомки потомков корня дерева и т.д.
Поддерево – часть древообразной структуры данных, которая может быть представлена в виде отдельного дерева.
Степенью вершины в дереве называется количество дуг, которое из нее выходит. Степень дерева равна максимальной степени вершины, входящей в дерево . При этом листьями в дереве являются вершины, имеющие степень нуль. По величине степени дерева различают два типа деревьев:
Упорядоченное дерево – это дерево , у которого ветви, исходящие из каждой вершины, упорядочены по определенному критерию.
Деревья являются рекурсивными структурами, так как каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:
Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.
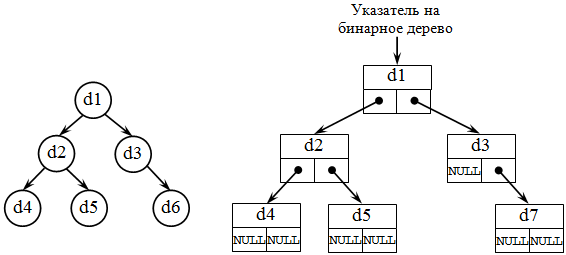
Списочное представление деревьев основано на элементах, соответствующих вершинам дерева. Каждый элемент имеет поле данных и два поля указателей: указатель на начало списка потомков вершины и указатель на следующий элемент в списке потомков текущего уровня. При таком способе представления дерева обязательно следует сохранять указатель на вершину, являющуюся корнем дерева .
Для того, чтобы выполнить определенную операцию над всеми вершинами дерева необходимо все его вершины просмотреть. Такая задача называется обходом дерева.
Обход дерева – это упорядоченная последовательность вершин дерева, в которой каждая вершина встречается только один раз.
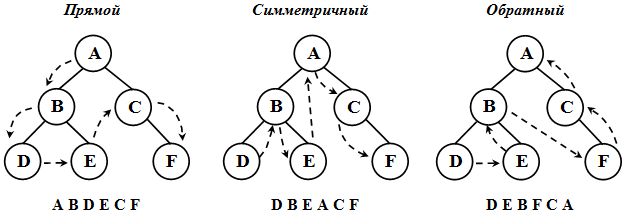
При обходе все вершины дерева должны посещаться в определенном порядке. Существует несколько способов обхода всех вершин дерева. Выделим три наиболее часто используемых способа обхода дерева ( рис. 31.2):
Существует большое многообразие древовидных структур данных. Выделим самые распространенные из них: бинарные (двоичные) деревья, красно-черные деревья, В-деревья, АВЛ-деревья , матричные деревья, смешанные деревья и т.д.
Бинарные деревья
Бинарные деревья являются деревьями со степенью не более двух.
Бинарное (двоичное) дерево – это динамическая структура данных , представляющее собой дерево , в котором каждая вершина имеет не более двух потомков ( рис. 31.3). Таким образом, бинарное дерево состоит из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка .
Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут соответственно:
- информационное поле (ключ вершины);
- служебное поле (их может быть несколько или ни одного);
- указатель на левое поддерево ;
- указатель на правое поддерево .
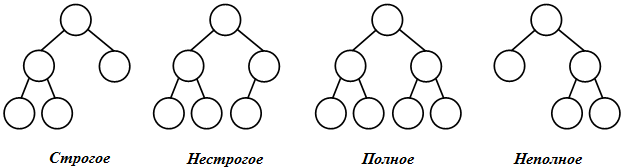
По степени вершин бинарные деревья делятся на ( рис. 31.4):
- строгие – вершины дерева имеют степень ноль (у листьев) или два (у узлов);
- нестрогие – вершины дерева имеют степень ноль (у листьев), один или два (у узлов).
В общем случае у бинарного дерева на k -м уровне может быть до 2 k-1 вершин. Бинарное дерево называется полным, если оно содержит только полностью заполненные уровни. В противном случае оно является неполным.
Дерево называется сбалансированным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.
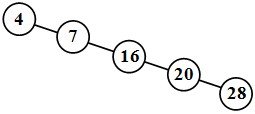
Бинарное дерево может представлять собой пустое множество . Бинарное дерево может выродиться в список ( рис. 31.5).
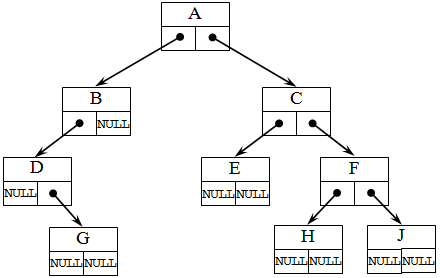
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, ‘*’ (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева , представленного на следующем рисунке 6, входной поток имеет вид: ABD*G***CE**FH**J** .
Бинарные деревья могут применяться для поиска данных в специально построенных деревьях ( базы данных ), сортировки данных, вычислений арифметических выражений , кодирования (метод Хаффмана) и т.д.
Источник
Древовидная структура — Tree structure
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. ( Июль 2014 г. ) (Узнайте, как и когда удалить этот шаблон сообщения)
Оригинал Энциклопедия использовал древовидную диаграмму, чтобы показать, как были упорядочены его предметы.
А древовидная структура или же древовидная диаграмма это способ представления иерархический природа структура в графической форме. Он назван «древовидной структурой», потому что классический представление напоминает дерево, хотя диаграмма обычно перевернута по сравнению с биологическим деревом: «стебель» вверху, а «листья» внизу.
Древовидная структура концептуальна и представлена в нескольких формах. Для обсуждения древовидной структуры в определенных полях см. Дерево (структура данных) для информатики: что касается теории графов, см. дерево (теория графов), или также дерево (теория множеств). Перечислены другие статьи по теме.
Терминология и свойства
Элементы дерева называются «узлы «. Линии, соединяющие элементы, называются» ветвями «. Узлы без дочерних элементов называются листовые узлы, «конечные узлы» или «листья».
Каждый конечный древовидная структура имеет член, не имеющий начальство. Этот член называется «корнем» или корневой узел. Корень — это начальный узел. Но обратное неверно: бесконечные древовидные структуры могут иметь или не иметь корневой узел.
Имена отношений между узлами моделируют терминология родства семейных отношений. Гендерно-нейтральные имена «родитель» и «ребенок» в значительной степени вытеснили старые термины «отец» и «сын». Термин «дядя» по-прежнему широко используется для других узлов на том же уровне, что и родительский, хотя иногда его заменяют нейтральными с гендерной точки зрения терминами, такими как «оммер». [1]
- «Родитель» узла — это узел на одну ступень выше в иерархии (то есть ближе к корневому узлу) и лежащий на той же ветви.
- «Родственные» («брат» или «сестра») узлы совместно используют один и тот же родительский узел.
- «Дяди» узла (иногда «оммеры») являются братьями и сестрами родительского узла.
- Узел, который связан со всеми узлами нижнего уровня, называется «предком». Подключенные узлы нижнего уровня являются «потомками» узла-предка.
В данном примере «энциклопедия» является родоначальником «науки» и «культуры», своих детей. «Искусство» и «ремесло» — это братья и сестры и дети «культуры», которая является их родителем и, следовательно, одним из их предков. Кроме того, «энциклопедия», как корень дерева, является родоначальником «науки», «культуры», «искусства» и «ремесла». Наконец, «наука», «искусство» и «ремесло», как листья, не являются предками ни одного другого узла.
Древовидные структуры могут изображать все виды таксономический знания, такие как родословные, биологический эволюционное дерево, то эволюционное древо языковой семьи, то грамматическая структура языка (ключевым примером является S → NP VP, что означает, что предложение представляет собой именную фразу и глагольную фразу, каждая из которых, в свою очередь, имеет другие компоненты, которые имеют другие компоненты), то, как веб-страницы логически упорядочены на веб-сайте, математические деревья целочисленных множеств и так далее.
В Оксфордский словарь английского языка записывает использование терминов «древовидная структура» и «древовидная диаграмма» с 1965 г. в Ноам Хомский с Аспекты теории синтаксиса. [2]
В древовидной структуре есть один и только один дорожка из любой точки в любую другую.
Информатика широко использует древовидные структуры (видеть Дерево (структура данных) и телекоммуникации.)
Формальное определение см. теория множеств, и для обобщения, в котором дети не обязательно являются преемниками, см. порядок префиксов.
Примеры древовидных структур
информационная диаграмма в форме дерева, иллюстрирующая «эволюцию» термоэмиссионных трубок (разновидность вакуумных трубок) между 1883 и 1934 годами.
- Интернет:
- иерархия usenet
- Объектная модель документа логическая структура, [3]Yahoo! предметный указатель, Керли
- двоичное дерево поиска
- красно-черное дерево
- AVL дерево
- R-дерево
- (Синтаксис) Деревья структуры фраз
- (Историческая лингвистика) Модель дерева изменения языка
Представляя деревья
Существует много способов визуального представления древовидной структуры, почти всегда они сводятся к вариациям или комбинациям нескольких основных стилей:
Классические схемы узловых связей
Классические схемы узловых соединений, которые соединяют узлы вместе с отрезками линий:
Вложенные наборы
Вложенные наборы которые используют изоляцию / сдерживание, чтобы показать отцовство, примеры включают Карты деревьев и фрактальные карты:
Многослойные схемы «сосульки»
Многослойные диаграммы «сосульки», использующие выравнивание / смежность.
Контуры и виды дерева
Списки или диаграммы, в которых используется отступ, иногда называемый «очертания » или же «виды деревьев «.
Источник