6.1 Физическое представление древовидных структур
Рассмотрим простой двумерный файл, в котором каждая запись содержит один и тот же набор элементов данных. Этот файл физически может быть представлен последовательно. Однако атрибуты, связанные с одним описываемым объектом, могут иметь несколько значений. На рис. 6.1 представлен файл, в котором хранятся расценки на изделия, закупаемых у различных поставщиков. Нарушение двумерности происходит из-за того, что некоторые поставщики устанавливают специальные скидки в зависимости от количества продаваемых изделий. В некоторых записях будет одно поле ТОРГОВАЯ-СКИДКА, в других их может быть несколько. Рис.6.1 Рис.6.2 Если используются записи переменной длины, то включение в запись РАСЦЕНКА переменного числа полей ТОРГОВАЯ-СКИДКА не представляет трудностей. Однако большинство существующих систем программного обеспечения позволяет работать только с записями постоянной длины, поэтому разработчик должен решить, сколько полей ТОРГОВАЯ-СКИДКА должно быть зарезервировано в записи РАСЦЕНКА. У разработчика имеются три возможности.
58 Во-первых, он может зарезервировать в записи РАСЦЕНКА место для 20 значений поля ТОРГОВАЯ-СКИДКА. В этом случае память будет использоваться неэффективно, поскольку в большинстве записей число значений этого поля будет меньше 20. Во-вторых, он может ввести отдельную запись для каждой торговой скидки. Запись РАСЦЕНКА будет содержать указатель на записи ТОРГОВАЯСКИДКА (рис. 6.2). В этом случае при обращении к записи ТОРГОВАЯСКИДКА всегда используется дополнительный поиск на внешнем запоминающем устройстве. В-третьих, разработчик может зарезервировать в записи РАСЦЕНКА место для нескольких значений поля ТОРГОВАЯ-СКИДКА и дополнительно ввести запись переполнения для случаев, когда зарезервированного места будет недостаточно. При этом возникают некоторые вопросы, например: сколько значений поля ТОРГОВАЯ-СКИДКА следует размещать в записи РАСЦЕНКА? На рис. 6.3 приведены две типичные кривые, отражающие изменение объема памяти и дополнительного времени поиска в зависимости от числа сегментов ТОРГОВАЯ-СКИДКА, включенных в основную запись РАСЦЕНКА. Если для данных ТОРГОВАЯ-СКИДКА место в основной записи не резервируется (рис. 6.2), то для получения записи ТОРГОВАЯ-СКИДКА в случае, когда общее число записей равно 1000, требуется дополнительно 56 с. В другом крайнем случае, когда в записи РАСЦЕНКА зарезервировано место для 20 значений поля ТОРГОВАЯ-СКИДКА, дополнительного времени для доступа не требуется, однако объем памяти увеличится на 200 000 байтов для 1000 записей. Из рис. 6.3 видно, что наиболее приемлемое решение заключается в резервировании в записи РАСЦЕНКА места для четырех значений поля ТОРГОВАЯ-СКИДКА. Этого оказывается достаточно для записи информации о большинстве изделий в нашем примере, а в тех случаях, когда четырех значений поля оказывается недостаточно, используются записи переполнения, в которых хранятся остальные значения агрегата ТОРГОВАЯ-СКИДКА.
6.1.2 ГЛАВНЫЙ И ДЕТАЛЬНЫЙ ФАЙЛЫ
На рис. 6.2 и 6.4 приведены примеры простых двухуровневых файлов. В системах обработки данных двухуровневые файлы используются часто; например, для банковской системы используются записи счетов клиентов и записи о сделках клиентов. Эти записи обычно рассматриваются соответственно как главные и детальные записи и изображаются в виде двухуровневого дерева. Для любого такого файла или для любой пары уровней дерева разработчик имеет возможность выбора степени включения некоторых сегментов нижнего уровня в сегменты верхнего уровня. Обычно все сегменты нижнего уровня размещаются отдельно от сегментов верхнего уровня или же объединяются с ними. Однако при использовании графиков, показанных на рис. 24.3, можно найти компромиссное решение (рис. 6.4), которое может оказаться лучше решения, найденного по принципу все или ничего.
6.1.3 МНОГОУРОВНЕВЫЕ ДЕРЕВЬЯ
Запись расценок, показанная на рис. 6.4, фактически может быть поддеревом более обширной структуры. База данных закупок может содержать много записей ПОСТАВЩИК, и каждая запись ПОСТАВЩИК может иметь несколько записей РАСЦЕНКА, которые в свою очередь могут содержать несколько агрегатов ТОРГОВАЯ-СКИДКА. Такую базу данных можно представить в виде трехуровневого дерева (рис. 6.5). Рис. 6.5 На рис. 6.6 показана схема и два экземпляра схемы трехуровневого дерева. Остальные рисунки в этой главе иллюстрируют способы, при помощи которых это дерево может быть физически реализовано.
6.1.4 Метод 1. Физически последовательное размещение
В течение первых двух десятилетий существования вычислительной техники большинство файлов располагалось последовательно на картах или лентах. При этом древовидные структуры обычно представлялись посредством
60 физически последовательного размещения данных на носителях. На рис. 6.7 с помощью этого метода представлено дерево, изображенное на рис. 6.6. Последовательность элементов на рис. 6.7 иногда называется левосписковой структурой; иногда ее называют последовательностью типа сверху вниз и слева направо. Она является основой иерархически последовательного метода доступа (HSAM) фирмы IBM. Рис.6.6 Рис.6.7 Последовательность строится следующим образом: выбираются узлы, начиная от вершины, дерева и вниз по самой левой ветви дерева’, когда выбран узел самого нижнего уровня этой ветви, выбираются подобные узлы слева направо; процесс повторяется, причем уже выбранные узлы пропускаются. При размещении каждой записи последовательности в памяти может указываться, к какому уровню дерева она относится. Это выполняется путем введения в каждую запись специального кода; так, например, тип записи может быть определен из ключа. Возможно также использование некоторой формы разграничения последовательности записей, например представление записи в таком виде: А (В (С С С ) В ( С С ) В ( С С С С )).
Источник
Деревья. Двоичные деревья.
Пусть Т – некоторый тип данных. Деревом типа Т называется структура, образованная элементом типа Т (корнем) и конечным (возможно пустым) множеством с переменным числом элементов – деревьев типа Т (поддеревьев)
Приведём определения, относящиеся к дереву: а) элементы типа Т, входящие в дерево называют узлами (вершинами) б) число поддеревьев данного узла называют его степенью в) узел, не имеющий поддеревьев, называют листом (концевым узлом) г) уровень в дереве определяется рекурсивно: уровень корня каждого поддерева данного узла на “1” больше уровня донного узла; уровень корня всего дерева = 1. д) уровень дерева – макс. Уровень его вершин.
Если порядок сыновей существенен, то сыновей упорядочивают “по старшенству” (подобно очереди), т.е. чем больше номер, тем дальше от предка. Определённые таким образом деревья называют деревьями общего вида.
Двоичное (бинарное) дерево – конечное множество узлов, которое или пусто, или состоит из корня и 2х непересекающихся поддеревьев (левое и правое) (Пример:схема спортивного турнира)
Предком для узла x называется узел дерева, из которого существует путь в узел x. Потомком узла x называется узел дерева, в который существует путь (по стрелкам) из узла x.
Родителем для узла x называется узел дерева, из которого существует непосредственная дуга в узел x.
Сыном узла x называется узел дерева, в который существует непосредственная дуга из узла x. Уровнем узла x называется длина пути (количество дуг) от корня к данному узлу.
Листом дерева называется узел, не имеющий потомков. Внутренней вершиной называется узел, имеющий потомков. Высотой дерева называется максимальный уровень листа дерева. Упорядоченным деревом называется дерево, все вершины которого упорядочены (то есть имеет значение последовательность перечисления потомков каждого узла
23 Двоичное дерево. Функциональная спецификация
Пусть BTt -двоичное дерево компонент типа T. Он характеризуется следующими операциями: а) создать (всегда создаётся пустое дерево) б) проверка на пустоту в) построить дерево (из корня и 2х поддеревьев) г) получение корня д) получение левого/правого поддеревьев е) уничтожение дерева
Возможные операции над деревьями: а) чтение данных из узла б) создание дерева, состоящего из одного корня в) построение дерева из заданных корня и поддеревьев г) присоединение нового поддерева к узлу д) замена поддерева на новое е) удаление поддерева ё) получение узла, следующего за данным в определённом порядке
24 Двоичное дерево. Логическое описание. Построение и визуализация
Тип данных дерево обычно отсутствует в универсальных языках программирования, и нужно его моделировать программно. Так же, как и в списках, цепная структура дерева будет состоять из динамически порождаемых элементов, в которых предусмотрены ссылки на очередные компоненты структуры:
struct node* 1;
struct node* r; >
Динамическая структура выглядит так: >>>>>>>
Рассмотрим программу построения дерева из n вершин, значения которых поступают из входного текстового файла input. Если нам нужно построить из этих вершин какое- нибудь дерево, то можно первую из них сделать корнем, вторую правым поддеревом, третью правым поддеревом правого поддерева, и т. д. В результате получим линейное дерево (список) максимальной глубины (n). Интереснее обратная задача: построить из этих же вершин дерево минимальной глубины. Для этого при построении дерева надо добиться его равномерного заполнения (ау. сплошное турнирное представление!), размещая приходящие вершины поровну слева и справа от каждой вершины по следующему рекурсивному(!) правилу:
1)взять одну вершину в качестве корня:
2)построить тем же способом левое поддерево с = nl div 2 вершинами;
3)построить тем же способом правое поддерево с nr = n — nl — 1 вершиной.
25 Двоичное дерево. Физическое представление. Прошивка.
На массиве: цельный кусок памяти, на первом месте корень, на 2м и 3м – его левый и правый сыновья, а далее – по паром сыновья каждого родителя, т.е. Сыновья i-го родителя лежат на местах 2i и 2i+1 (j-ый элемент i-го уровня находится на месте 2^(j-1) + j – 1.
Основным неудобством сплошного представления дерева является высокая цена вставки и удаления элементов + перерасход памяти.
Для деревьев можно использовать рекурсивные ссылочные представления, которые были разработаны для списков, но с той лишь разницей, что указатели вперёд и назад по линейной структуре теперь направляются к левому и к правому поддеревьям соответственно.
Динамическая структура: каждый элемент указывает на место своих сыновей
Прошитые бинарные деревья – В прошитых бинарных деревьях вместо пустых указателей используются специальные связи-нити и каждый указатель в узле дерева дополняется однобитовым признаком ltад и rtag, соответственно. Признак определяет, содержится ли в соответствующем указателе обычная ссылка на поддерево или в нем содержится связь-нить.
Связь-нить – в поле l указывает на узел-предшественник при обратном обходе, а в поле r – на узел-приемник.
Для прошитых деревьев можно выполнить не рекурсивный обход без использования стека.
Прошитое дерево линеаризовано и может быть помещено в очередь или список => можно применить итераторы для обработки, т.к функциональность совпадает.
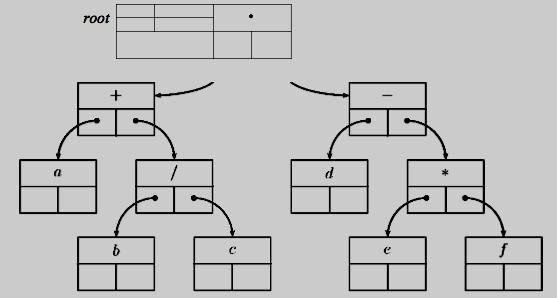
Среди прошитых деревьев важный класс составляют правопрошитые деревья, т. е. прошитые бинарные деревья, у которых используется только правая связь-нить, а в поле / содержится либо обычный указатель, либо пустой указатель. Поле ltag в таком случае не используется. (картинка справа: дерево для арифметических операций)

26 Алгоритмы обхода деревьев.
Обход дерево – просматривание дерева по определённому алгоритму так, что все вершины будут просмотрены.
I прямой обход (сверху вниз; КЛП; корень прежде; preorder) 1) если дерево пусто – конец обхода 2) берём корень 3) обходим левое поддерево 4) обходим правое поддерево
II обратный обход (слева направо; ЛКП; корень между; inorder) 1) если дерево пусто – конец обхода 2)обходим левое поддерево 3) берём корень 4)обходим правое поддерево
III концевой обход (снизу вверх; ЛПК; корень в конце; posorder) 1) если дерево пусто – конец обхода 2) обходим левое поддерево 3) обходим правое поддерево 4) берём корень
I поиск в глубину: 1) если дерево пусто – конец обхода
2) берём корень 3) ищем в глубину для поддерева старшего сына 4) ищем в глубину для поддерева следующего брата
II поиск в ширину: 1) поместить в пустую очередь корень дерева 2) если очередь узлов пуста – конец обхода 3) извлечь первый элемент из очереди и поместить в конец всех его сыновей 4) вернуться к п. 2)
Источник