Двоичный код дерева графа

Лекция № 14. Деревья

1. Основные определения

Дерево – связный граф без циклов. Лес (или ациклический граф) – неограф без циклов. Компонентами леса являются деревья. Теорема 14.1.Для неографаGсnвершинами без петель следующие условия эквивалентны:

1. G– дерево;
2. G– связной граф, содержащийn– 1 ребро;
3. G– ациклический граф, содержащийn– 1 ребро;
4. Любые две несовпадающие вершины графаGсоединяет единственная цепь;
5. G– ациклический граф, такой, что если в него добавить одно ребро, то в нем появится ровно один цикл.

Теорема 14.2.НеографGявляется лесом тогда и только тогда, когда коранг графаv(G)=0. Висячая вершина в дереве – вершина степени 1. Висячие вершины называются листьями, все остальные – внутреннимивершинами. Если в дереве особо выделена одна вершина, называемая корнем, то такое дерево называется корневым, иначе – свободным. Корневое дерево можно считать орграфом с ориентацией дуг из корня или в корень. Очевидно, что для любой вершины корневого дерева, кроме корня, . Для корня, для листьев. Вершины дерева, удаленные на расстояние k (в числе дуг) от корня, образуют k-й ярус (уровень) дерева. Наибольшее значение k называется высотой дерева. Если из какой-либо вершины корневого дерева выходят дуги, то вершины на концах этих дуг называют сыновьями (в английской литературе – дочери (daughter)).

1. Центроид дерева

Ветвь к вершине v дерева – это максимальный подграф, содержащий v в качестве висячей вершины. Вес вершиныk – наибольший размер ее ветвей. Центроид (или центр масс) дерева C – множество вершин с наименьшим весом: C = v| c(v) = >. Вес любого листа дерева равен размеру дерева. Высота дерева с корнем, расположенным в центроиде, не больше наименьшего веса его вершин. Свободное дерево порядка n с двумя центроидами имеет четное количество вершин, а вес каждого центроида равен n/2. Теорема 14.3 (Жордана).Каждое дерево имеет центроид, состоящий из одной или двух смежных вершин.Пример 14.1. Найти наименьший вес вершин дерева, изображенного на рис. 14.1, и его центроид. Рис. 14.1 Решение. Очевидно, что вес каждой висячей вершины дерева порядка n равен n – 1. Висячие вершины не могут составить центроид дерева, поэтому исключим из рассмотрения вершины 1, 2, 4, 6, 12, 13 и 16. Для всех остальных вершин найдем их вес, вычисляя длину (размер) их ветвей. Число ветвей вершины равно ее степени. Вершины 3, 5 и 8 имеют по две ветви, размеры которых равны 1 и 14. К вершине 7 подходят четыре ветви размером 1, 2, 2 и 10. Таким образом, ее вес . Аналогично вычисляются веса других вершин:,,. Минимальный вес вершин равен 8, следовательно, центроид дерева образуют две вершины с таким весом: 11 и 15.

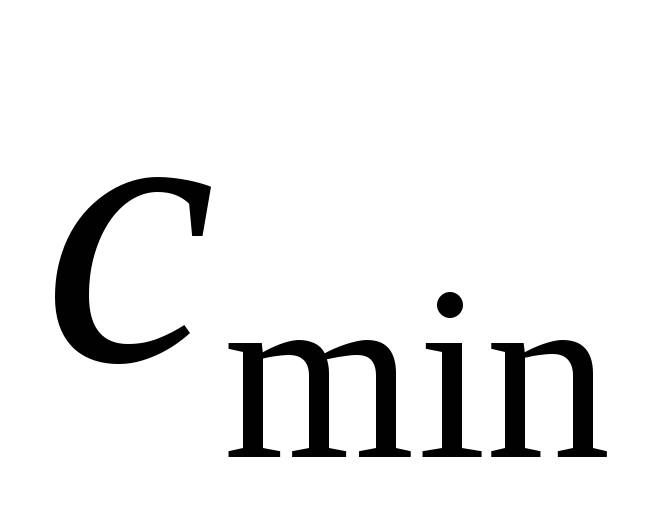
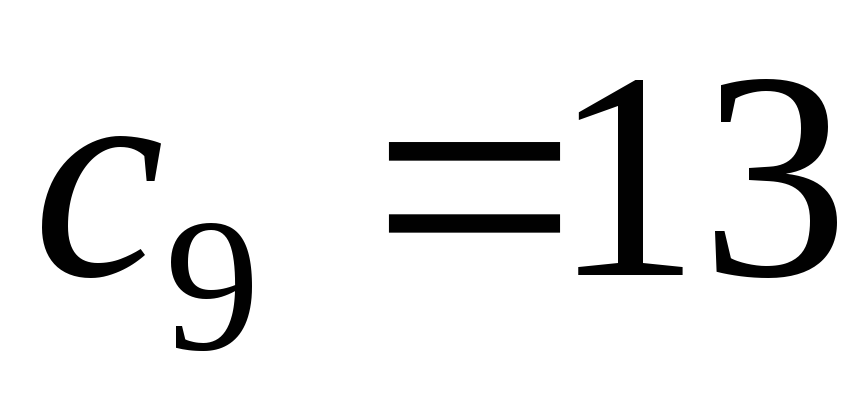
1. Десятичная кодировка

Деревья представляют собой важный вид графов. С помощью деревьев описываются базы данных, деревья моделируют алгоритмы и программы, их используют в электротехнике, химии. Одной из актуальных задач в эпоху компьютерных и телекоммуникационных сетей является задача сжатия информации. Сюда входит и кодировка деревьев. Компактная запись дерева, полностью описывающая его структуру, может существенно упростить как передачу информации о дереве, так и работу с ним. Существует множество способов кодировки деревьев. Рассмотрим одну из простейших кодировок помеченных деревьев с выделенным корнем – десятичную. Кодируя дерево, придерживаемся следующих правил.

1. Кодировка начинается с корня и заканчивается в корне.
2. Каждый шаг на одну дугу от корня кодируется единицей.
3. В узле выбираем направление на вершину с меньшим номером.
4. Достигнув листа, идем назад, кодируя каждый шаг нулем.
5. При движении назад в узле всегда выбираем направление на непройденную вершину с меньшим номером.

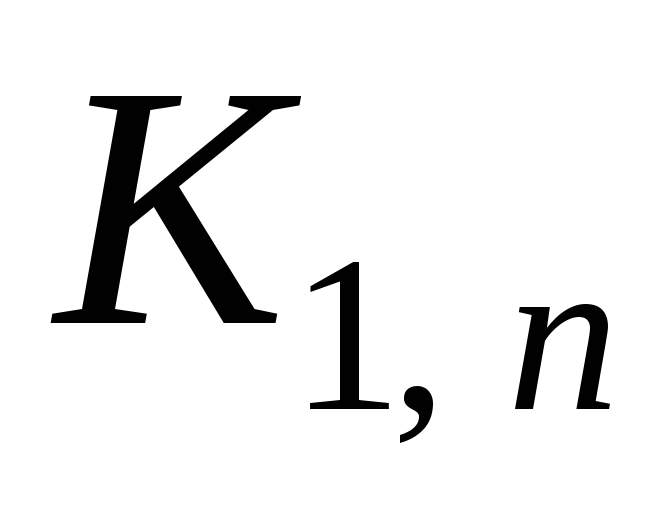
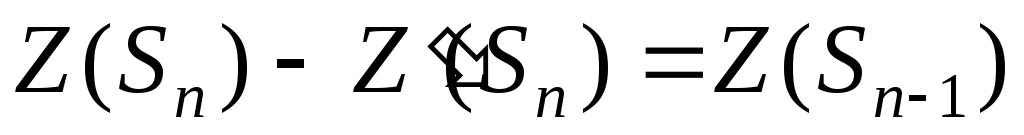
Кодировка в такой форме получается достаточно компактной, однако она не несет в себе информации о номерах вершин дерева. Существуют аналогичные кодировки, где вместо единиц в таком же порядке проставляются номера или названия вершин. Есть деревья, для которых несложно вывести формулу десятичной кодировки. Рассмотрим, например, графы-звезды , являющиеся полными двудольными графами, одна из долей которых состоит из одной вершины. Другое обозначение звезд –. На рис. 14.2 показаны звезды, а также приведены их двоичные и десятичные кодировки. Корень дерева располагается в центральной вершине звезды. Легко получить общую формулу: . (14.1) Рис. 14.2 Если корень поместить в любой из висячих вершин, то код такого дерева будет выражаться большим числом. Более того, существует зависимость. Аналогично рассматриваются и цепи (рис. 14.3). Цепи обозначаются как. Рис. 14.3 В звездах только два варианта расположения корня с различными десятичными кодировками. В цепи же число вариантов кодировок в зависимости от положения корня растет с увеличением n. Рассмотрим самый простой вариант, расположив корень в концевой вершине (листе). Для получим двоичную кодировку 10 и десятичную 2, для– 1100 и 12, для– 111000 и 56, для– 11110000 и 240. Общая формула для десятичной кодировки цепи с корнем в концевой вершине имеет вид . (14.2) Пример 14.2. Записать десятичный код дерева, изображенного на рис. 14.4, с корнем в вершине 3. Рис. 14.4 Решение. На основании правила кодировки, двигаясь по дереву, проставим в код единицы и нули. При движении из корня 3 к вершине 7 проходим четыре ребра. В код записываем четыре единицы: 1111. Возвращаясь от вершины 7 к вершине 2 (до ближайшей развилки), проходим три ребра. Записываем в код три нуля: 000. От вершины 2 к 5 и далее к 8 (меньший номер): 11; от 8 назад к 5 и от 5 к 9: 01; от 9 к корню 3: 000. И, наконец, от 3 к 6 и обратно: 10. В итоге, собирая все вместе, получим двоичный код дерева: 1 111 000 110 100 010. Разбивая число на тройки, переводим полученное двоичное представление в восьмеричное. Получаем . Затем переводим это число в десятичное:.

Для продолжения скачивания необходимо пройти капчу:

Источник

3.10. Кодирование деревьев

Выделим в дереве какую-нибудь одну вершину, которую назовем корнем. Полученное дерево с выделенной вершиной называетсякорневым.

Для задания (с точностью до изоморфизма) корневыхдеревьев используюткод из 0 и 1, который мы определим индуктивно.

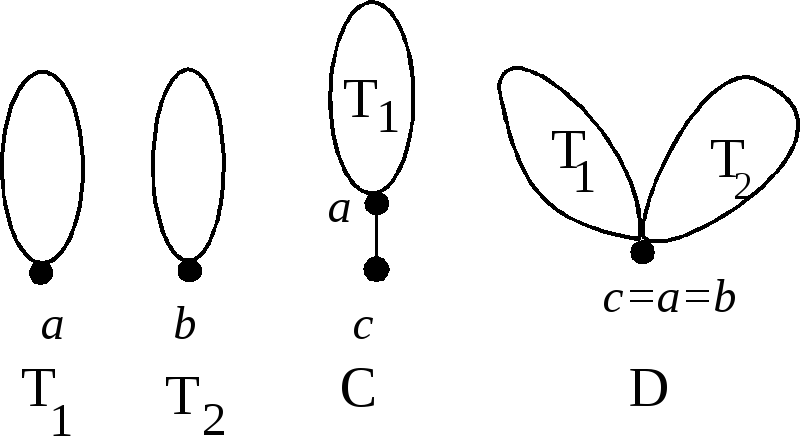
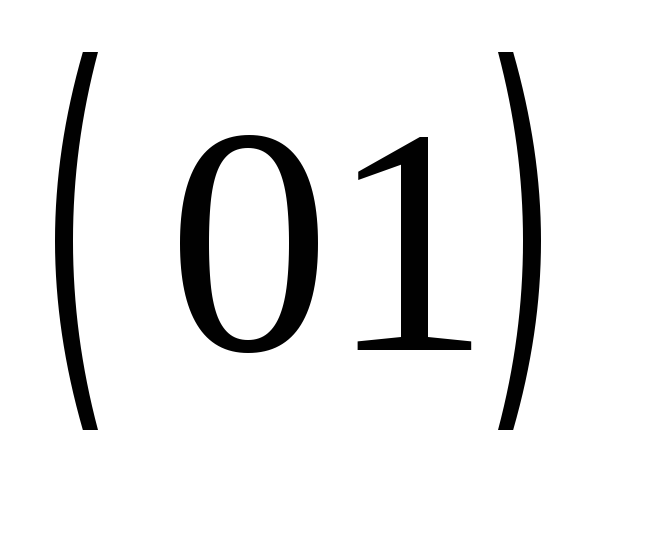
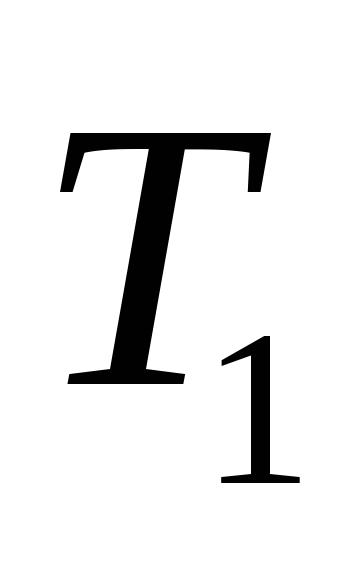
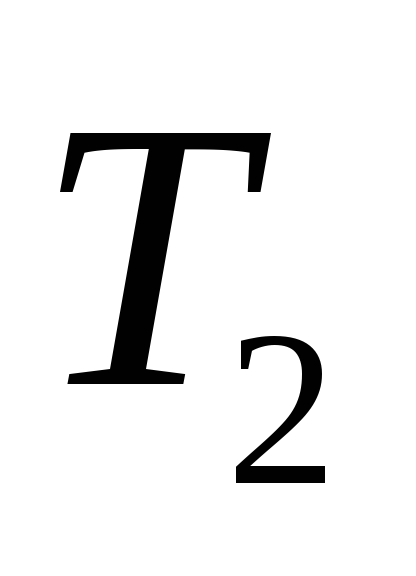
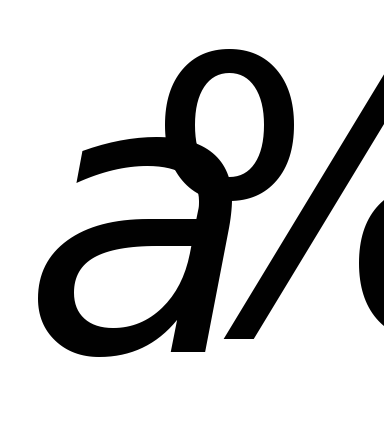
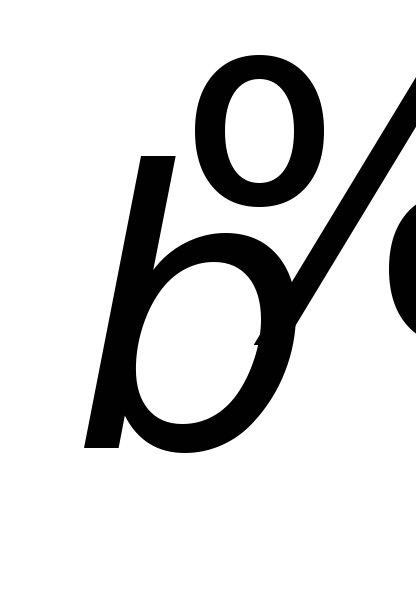
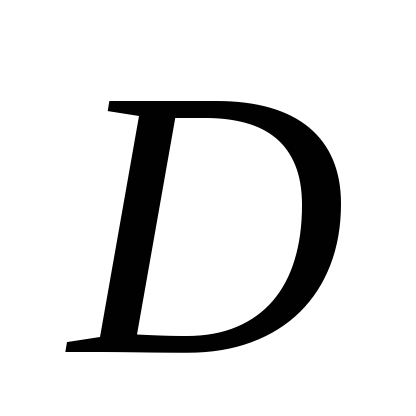
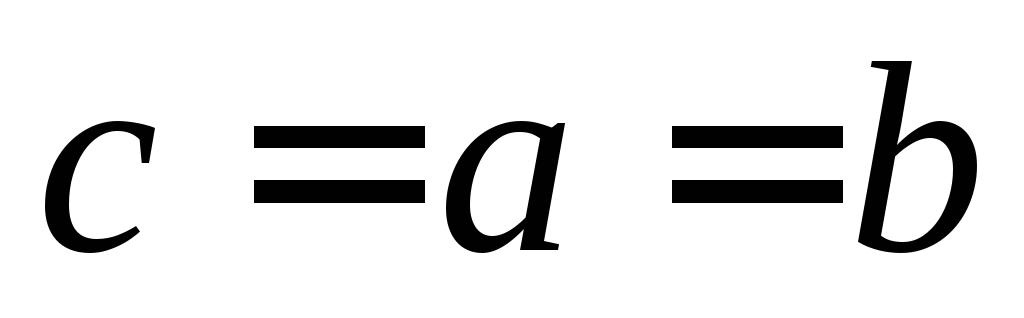
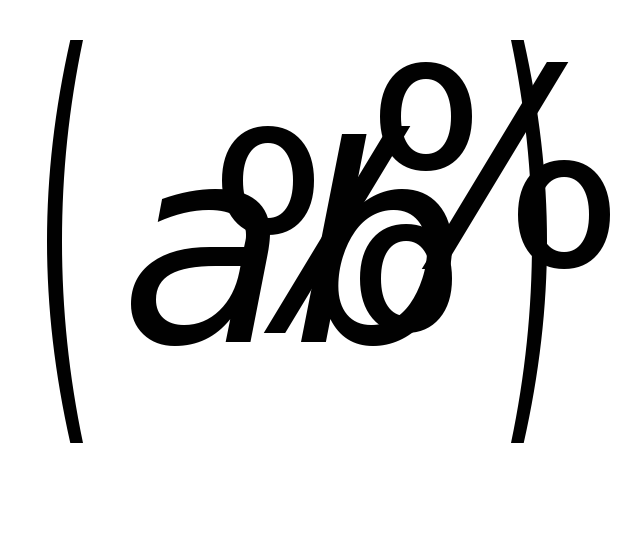
Определение.Кодом корневого дерева с одним ребром является .Пусть деревья и с корнямиa и b соответственно (см. рис.) имеют коды и .Тогда кодом дерева с корнем с является код , а кодом дерева с корнем — код.

Пример 1. Написать код дерева, изображенного на рисунке.

И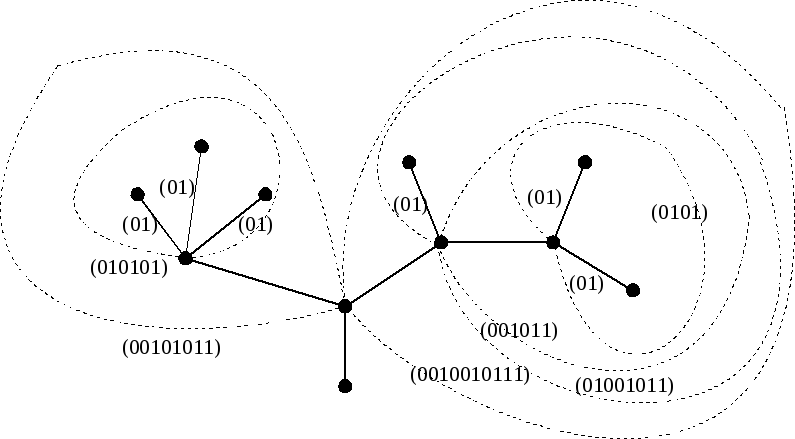так, код дерева —.

Справедливо следующее утверждение:для того, чтобы последовательность нулей и единиц являлась кодом некоторого дерева необходимо и достаточно, чтобы число нулей и единиц в этой последовательности было одинаковым, причем в любом начальном отрезке последовательности количество нулей было не меньше количества единиц.

Чтобы построить корневое дерево по кодуиз нулей и единиц, нужно разбить последовательность на пары 0 и 1, следуя правилу: первая попавшаяся в коде единица образует пару с предшествующим нулем; каждая следующая единица образует пару с ближайшим слева неиспользованным нулем. Если образованные таким образом пары пометить снизу кода фигурными скобками, то каждая такая скобка будет соответствовать ребру графа.

П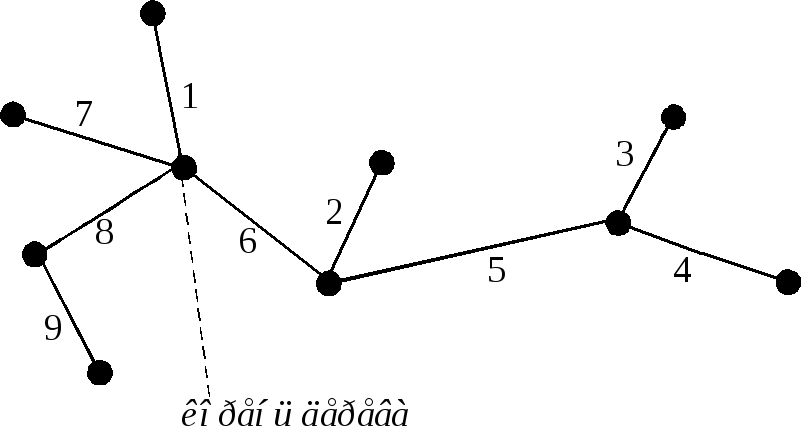ример 2.Построить дерево по коду.

Для задания помеченныхдеревьев, т.е. деревьев, вершины которых занумерованы, используют код из натуральных чисел.

Пусть дано помеченное дерево. Чтобы построить его код из натуральных чисел действуем следующим образом. Находим висячую вершину с наименьшим номером. Записываем номер смежной с ней вершины (это начало кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Для полученного в результате данной операции дерева находим висячую вершину с наименьшим номером, записываем номер смежной с ней вершины (это продолжение кода), после чего удаляем эту висячую вершину вместе с инцидентным ей ребром. Так поступаем до тех пор, пока не останется последнее ребро.

Заметим, что длина кода из натуральных чисел на единицу меньше числа ребер и на две единицы меньше числа вершин данного дерева.

Пример 3.На рисунке изображено помеченное дерево. Его код.

Построение дерева по коду из натуральных чиселрассмотрим на примере кода. Прежде всего, заметим, что дерево, которое нам предстоит построить, имеет 8 вершин.

Источник