Есть такие деревья информатика

Структуры данных: бинарные деревья. Часть 1

Этой статьей я начинаю цикл статей об известных и не очень структурах данных а так же их применении на практике.

В своих статьях я буду приводить примеры кода сразу на двух языках: на Java и на Haskell. Благодаря этому можно будет сравнить императивный и функциональный стили программирования и увидить плюсы и минусы того и другого.

Начать я решил с бинарных деревьев поиска, так как это достаточно базовая, но в то же время интересная штука, у которой к тому же существует большое количество модификаций и вариаций, а так же применений на практике.

Зачем это нужно?

Бинарные деревья поиска обычно применяются для реализации множеств и ассоциативных массивов (например, set и map в с++ или TreeSet и TreeMap в java). Более сложные применения включают в себя ropes (про них я расскажу в одной из следующих статей), различные алгоритмы вычислительной геометрии, в основном в алгоритмах на основе «сканирующей прямой».

В этой статье деревья будут рассмотрены на примере реализации ассоциативного массива. Ассоциативный массив — обобщенный массив, в котором индексы (их обычно называют ключами) могут быть произвольными.

Ну-с, приступим

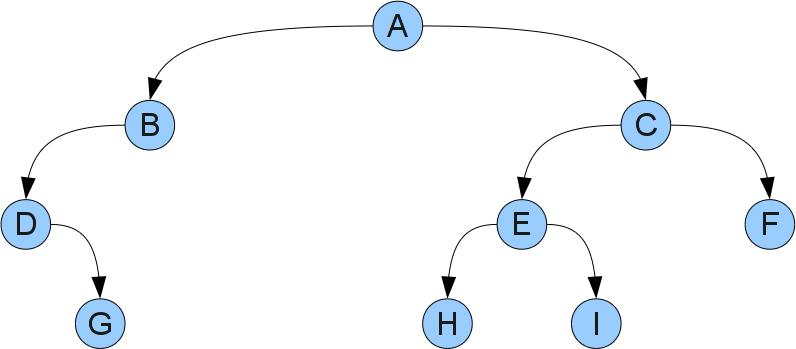
Двоичное дерево состоит из вершин и связей между ними. Конкретнее, у дерева есть выделенная вершина-корень и у каждой вершины может быть левый и правый сыновья. На словах звучит несколько сложно, но если взглянуть на картинку все становится понятным:

У этого дерева корнем будет вершина A. Видно, что у вершины D отсутствует левый сын, у вершины B — правый, а у вершин G, H, F и I — оба. Вершины без сыновей принято называть листьями.

Каждой вершине X можно сопоставить свое дерево, состоящее из вершины, ее сыновей, сыновей ее сыновей, и т.д. Такое дерево называют поддеревом с корнем X. Левым и правым поддеревьями X называют поддеревья с корнями соответственно в левом и правом сыновьях X. Заметим, что такие поддеревья могут оказаться пустыми, если у X нет соответствующего сына.

Данные в дереве хранятся в его вершинах. В программах вершины дерева обычно представляют структурой, хранящей данные и две ссылки на левого и правого сына. Отсутствующие вершины обозначают null или специальным конструктором Leaf:

data Ord key => BSTree key value = Leaf | Branch key value (BSTree key value) (BSTree key value) deriving (Show) 

static class Node  < T1 key; T2 value; Nodeleft, right; Node(T1 key, T2 value) < this.key = key; this.value = value; >> 

Как видно из примеров, мы требуем от ключей, чтобы их можно было сравнивать между собой ( Ord a в haskell и T1 implements Comparable в java). Все это не спроста — для того, чтобы дерево было полезным данные должны храниться в нем по каким-то правилам.

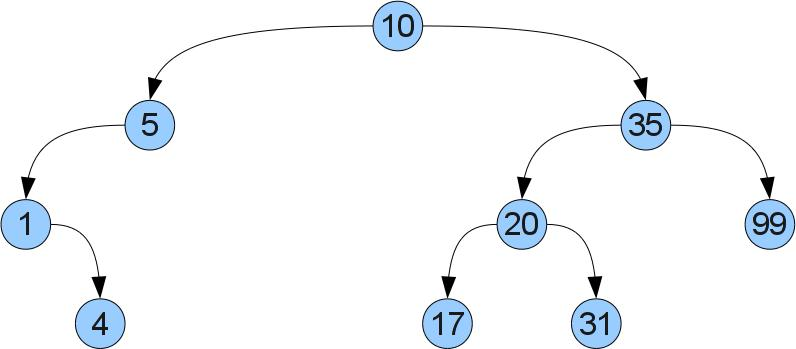
Какие же это правила? Все просто: если в вершине X хранится ключ x, то в левом (правом) поддереве должны храниться только ключи меньшие (соответственно большие) чем x. Проиллюстрируем:

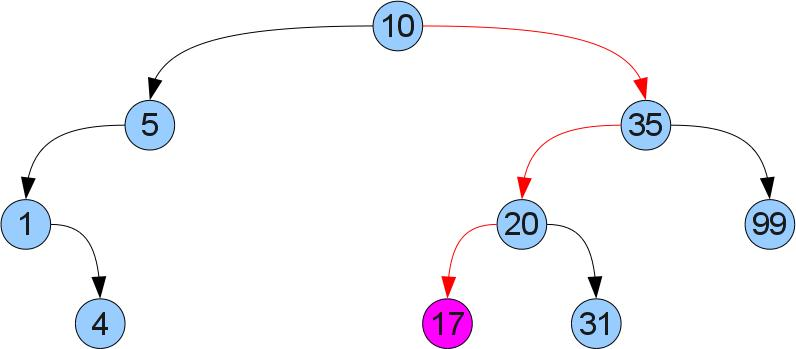
Что же нам дает такое упорядочевание? То, что мы легко можем отыскать требуемый ключ x в дереве! Просто сравним x со значением в корне. Если они равны, то мы нашли требуемое. Если же x меньше (больше), то он может оказаться только в левом (соответственно правом) поддереве. Пусть например мы ищем в дереве число 17:

Функция, получающая значение по ключу:

get :: Ord key => BSTree key value -> key -> Maybe value get Leaf _ = Nothing get (Branch key value left right) k | k < key = get left k | k >key = get right k | k == key = Just value 

public T2 get(T1 k) < Nodex = root; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < return x.value; >if (cmp < 0) < x = x.left; >else < x = x.right; >> return null; > 

Добавление в дерево

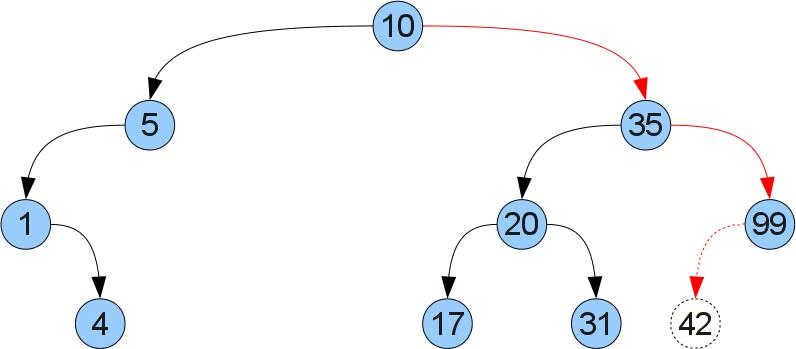
Теперь попробуем сделать операцию добавления новой пары ключ/значение (a,b). Для этого будем спускаться по дереву как в функции get, пока не найдем вершину с таким же ключем, либо не дойдем до отсутсвующего сына. Если мы нашли вершину с таким же ключем, то просто меняем соответствующее значение. В противно случае легко понять что именно в это место следует вставить новую вершину, чтобы не нарушить порядок. Рассмотрим вставку ключа 42 в дерево на прошлом рисунке:

add :: Ord key => BSTree key value -> key -> value -> BSTree key value add Leaf k v = Branch k v Leaf Leaf add (Branch key value left right) k v | k < key = Branch key value (add left k v) right | k >key = Branch key value left (add right k v) | k == key = Branch key value left right 

public void add(T1 k, T2 v) < Nodex = root, y = null; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < x.value = v; return; >else < y = x; if (cmp < 0) < x = x.left; >else < x = x.right; >> > Node newNode = new Node(k, v); if (y == null) < root = newNode; >else < if (k.compareTo(y.key) < 0) < y.left = newNode; >else < y.right = newNode; >> > 

Лирическое отступление о плюсах и минусах функционального подхода

Если внимательно рассмотреть примеры на обоих языках, можно увидеть некоторое различие в поведении функциональной и императивной реализаций: если на java мы просто модифицируем данные и ссылки в имеющихся вершинах, то версия на haskell создает новые вершины вдоль всего пути, пройденного рекурсией. Это связано с тем, что в чисто функциональных языках нельзя делать разрушающие присваивания. Ясно, что это ухудшает производительность и увеличивает потребляемую память. С другой стороны, у такого подхода есть и положительные стороны: отсутствие побочных эффектов сильно облегчает понимание того, как функционирует программа. Более подробно об этом можно прочитать в практически любом учебнике или вводной статье про функциональное программирование.

В этой же статье я хочу обратить внимание на другое следствие функционального подхода: даже после добавления в дерево нового элемента старая версия останется доступной! За счет этого эффекта работают ropes, в том числе и в реализации на императивных языках, позволяя реализовывать строки с асимптотически более быстрыми операциями, чем при традиционном подходе. Про ropes я расскажу в одной из следующих статей.

Вернемся к нашим баранам

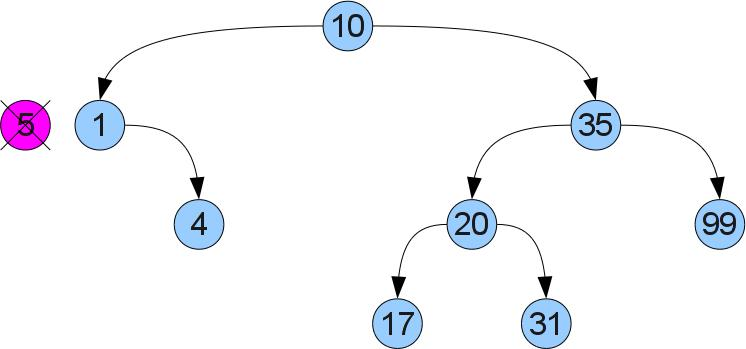
Теперь мы подобрались к самой сложной операции в этой статье — удалению ключа x из дерева. Для начала мы, как и раньше, найдем нашу вершину в дереве. Теперь возникает два случая. Случай 1 (удаляем число 5):

Видно, что у удаляемой вершины нет правого сына. Тогда мы можем убрать ее и вместо нее вставить левое поддерево, не нарушая упорядоченность:

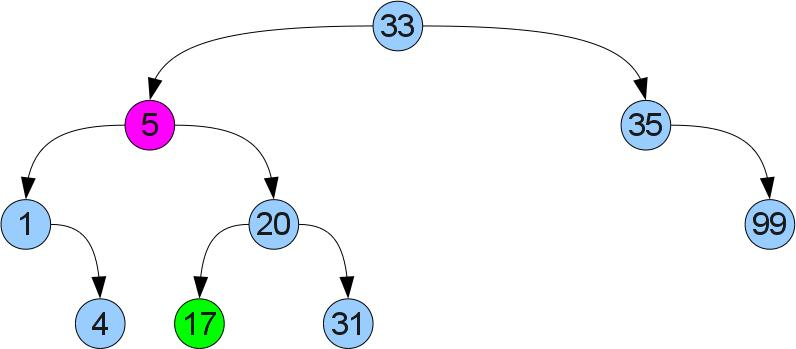
Если же правый сын есть, налицо случай 2 (удаляем снова вершину 5, но из немного другого дерева):

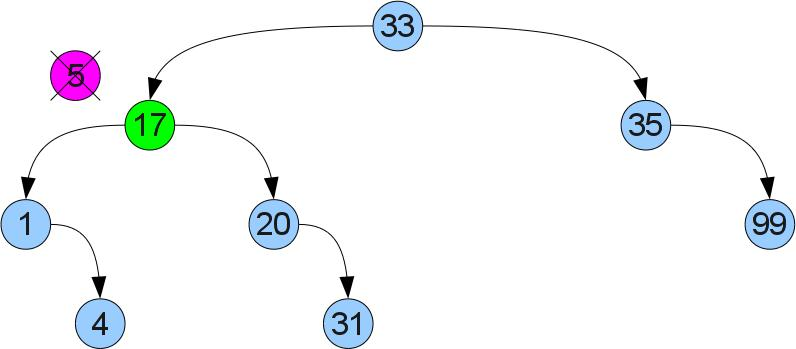
Тут так просто не получится — у левого сына может уже быть правый сын. Поступим по-другому: найдем в правом поддереве минимум. Ясно, что его можно найти если начать в правом сыне и идти до упора влево. Т.к у найденного минимума нет левого сына, можно вырезать его по аналогии со случаем 1 и вставить его вместо удалеемой вершины. Из-за того что он был минимальным в правом поддереве, свойство упорядоченности не нарушится:

remove :: Ord key => BSTree key value -> key -> BSTree key value remove Leaf _ = Leaf remove (Branch key value left right) k | k < key = Branch key value (remove left k) right | k >key = Branch key value left (remove right k) | k == key = if isLeaf right then left else Branch leftmostA leftmostB left right' where isLeaf Leaf = True isLeaf _ = False ((leftmostA, leftmostB), right') = deleteLeftmost right deleteLeftmost (Branch key value Leaf right) = ((key, value), right) deleteLeftmost (Branch key value left right) = (pair, Branch key value left' right) where (pair, left') = deleteLeftmost left 

public void remove(T1 k) < Nodex = root, y = null; while (x != null) < int cmp = k.compareTo(x.key); if (cmp == 0) < break; >else < y = x; if (cmp < 0) < x = x.left; >else < x = x.right; >> > if (x == null) < return; >if (x.right == null) < if (y == null) < root = x.left; >else < if (x == y.left) < y.left = x.left; >else < y.right = x.left; >> > else < NodeleftMost = x.right; y = null; while (leftMost.left != null) < y = leftMost; leftMost = leftMost.left; >if (y != null) < y.left = leftMost.right; >else < x.right = leftMost.right; >x.key = leftMost.key; x.value = leftMost.value; > > 

На десерт, пара функций, которые я использовал для тестирования:

fromList :: Ord key => [(key, value)] -> BSTree key value fromList = foldr (\(key, value) tree -> add tree key value) Leaf toList :: Ord key => BSTree key value -> [(key, value)] toList tree = toList' tree [] where toList' Leaf list = list toList' (Branch key value left right) list = toList' left ((key, value):(toList' left list)) 

Чем же все это полезно?

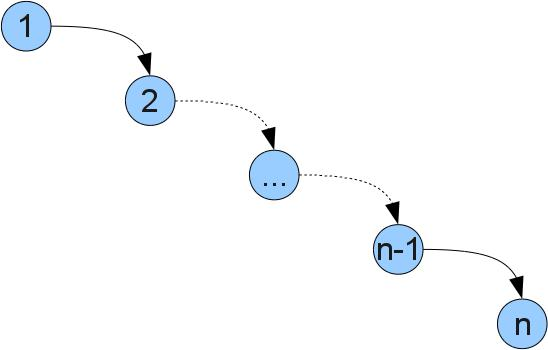
У читателя возможно возникает вопрос, зачем нужны такие сложности, если можно просто хранить список пар [(ключ, значение)]. Ответ прост — операции с деревом работают быстрее. При реализации списком все функции требуют O(n) действий, где n — размер структуры. (Запись O(f(n)) грубо говоря означает «пропорционально f(n)», более корректное описание и подробности можно почитать тут). Операции с деревом же работают за O(h), где h — максимальная глубина дерева (глубина — расстояние от корня до вершины). В оптимальном случае, когда глубина всех листьев одинакова, в дереве будет n=2^h вершин. Значит, сложность операций в деревьях, близких к оптимуму будет O(log(n)). К сожалению, в худшем случае дерево может выродится и сложность операций будет как у списка, например в таком дереве (получится, если вставлять числа 1..n по порядку):

К счастью, существуют способы реализовать дерево так, чтобы оптимальная глубина дерева сохранялась при любой последовательности операций. Такие деревья называют сбалансированными. К ним например относятся красно-черные деревья, AVL-деревья, splay-деревья, и т.д.

Анонс следующих серий

В следующей статье я сделаю небольшой обзор различных сбалансированных деревьев, их плюсы и минусы. В следующих статьях я расскажу о каком-нибудь (возможно нескольких) более подробно и с реализацией. После этого я расскажу о реализации ropes и других возможных расширениях и применениях сбалансированных деревьев.

Полезные ссылки

Исходники примеров целиком:

Также очень советую почитать книгу Кормен Т., Лейзерсон Ч., Ривест Р.: «Алгоритмы: построение и анализ», которая является прекрасным учебником по алгоритмам и структурам данных

Источник

Практическая работа в текстовом документе. Списки.

Существует два вида списков: нумерованный и маркированный. Их отличие заключается в том, что в нумерованном списке используются различные значки. А в маркированном одинаковые.

Для того чтобы добавить список необходимо выделить нужный фрагмент, а затем:

1. выбрать значок на панели инструментов для создания маркированного списка.
2. выбрать значок на панели инструментов для создания нумерованного списка.

Задание №1 Наберите предложенный текст. Создайте нумерованный список. Измените список на маркированный, подобрав самостоятельно вид маркера. Есть такие деревья.

1. Хлебное дерево из семейства тутовых.
2. Колбасное дерево из семейства бегониевых (кигелия).
3. Дерево путешественников из семейства банановых (Равенна мадагаскарская).
4. Шоколадное дерево (один из видов рода теоброма).
5. Конфетное дерево (говения).
6. Ландышевое дерево, растение рода клетра.
7. «Деревянная корова», растет в Коста-Рике.
8. Авокадо – аллигаторова груша из семейства лавровых.
9. Дынное дерево (папайя).
10. Железное дерево (железняк, парротия персидская).
11. Бумажное дерево, один из видов буссонетия.
12. Сальное дерево семейства молочных.
13. Мыльное дерево семейства сапиндовых.
14. Бутылочная тыква, горлянка (лагенария, посудная тыква).
15. Сапотовое дерево (саподилла).
16. Сейшельская пальма.
17. Базальтовое дерево.
18. Карандашное дерево (красный или виргинский можжевельник).
19. Рожковое дерево (цареградский стручок).
20. Вельвичия.
21. Индийский миндаль.
22. Гинкго.
23. Альмасига.
24. Драцена.
25. Баобаб.

1. древнегреческий философ,
2. религиозный и политический деятель,
3. основатель пифагореизма,
4. математик.

• свойств целых чисел и пропорций,
• доказательство теоремы Пифагора.

1. Паспорт кабинета (прошнурованный);
2. Обязанности (должностные) классного руководителя;
3. Обязанности (должностные) учителя;
4. Инструкция по заполнению журнала;
5. Типовое положение о материальной ответственности;
6. Выписка из приказа «О внутреннем трудовом распорядке работников школы № ____»
7. В кабинетах: химии, биологии, информатики, физики, физической культуры – инструкции по правилам техники безопасности (наличие журнала по ТБ);
8. Инструкция по работе с ТСО;
9. Календарно-тематическое планирование;
10. Расписание уроков (своих в кабинете);
11. Расписание звонков;
12. Расписание дополнительных и кружковых занятий;
13. График контрольных. Практических и лабораторных работ.

1. Проверьте орфографию. Выпишите в тетрадь список слов, предложенных к замене слова «лошки».

1. Выродов Павел 8Б лыжи
2. Фомина Яна 8В плавание
3. Квач Елена 8А волейбол

• В ходе соревнований техника безопасности не нарушалась.
• Призеры награждены грамотами и призами.
• Все временные рамки соблюдены.

Источник