Формула вычисления объема дерева

Стереометрические формулы для определения объёма ствола и его частей

Для определения объема ствола используют следующие приближенные формулы.

— простая формула Смалиана:

где g_o – площадь поперечного сечения у основания ствола, м 2 ;

g_L – площадь поперечного сечения ствола на расстоянии L, м 2 ;

L – длина отрезка ствола, м.

— формула срединного сечения или простая формула Губера:

где g_L/2 – площадь поперечного сечения на половине ствола, м 2 .

Если обозначить g_L/2 через γ, то простая формула Губера примет вид:

— простая формула Ньютона-Рикке:

— формула концевых сечений, или сложная формула Смалиана:

где g_o – площадь поперечного сечения у основания ствола, м 2 ;

g₁, g₂, g₃, g_n-1, g_n – площадь поперечного сечения ствола на концах n-метрового отрезка, м 2 ;

l – длина n метрового отрезка ствола, м.

— формула срединных сечений, или сложная формула Губера:

где γ₁, γ₂, γ_n, – площадь поперечного сечения на середине n-метрового отрезка, м 2 .

При делении ствола на отрезки длиной l остается вершина длиной h. Ее объем находят по формуле объема конуса.

Определение объёма круглых лесоматериалов по таблицам и формулам

Для определения объемов бревен, кряжей и других деловых круглых сортиментов могут быть использованы простые и сложные формулы определения объемов стволов и их частей. Наиболее широко при вычислении объемов круглого леса применяется простая формула срединного сечения или простая формула Губера. Для упрощения работы используют таблицы объемов отрезков стволов круглых лесоматериалов.

Результаты вычислений объемов в таких таблицах сгруппированы по длине бревен и диаметрам срединного сечения.

Видовые числа, коэффициенты формы, их практическое значение

Видовое число это отношение объема дерева или его части к объему цилиндра, имеющего высоту, равную высоте дерева, и основание, равное площади сечения ствола, взятое на той или иной высоте (h) в нижней части ствола. Чаще всего отрезок длиной h берут длиной 1,3 м. Такие видовые числа получили название старых видовых чисел. Они определяются по следующей формуле:

Видовые числа, найденные по данной формуле, имеют недостаток, связанный с тем, что при одной и той же форме ствола старые видовые числа будут различными по величине из-за разной высоты деревьев.

Когда поперечное сечение, служащее основанием для построения цилиндра, берется на высоте, выраженное в долях общей высоты дерева (H:20 или H:10), получаются видовые числа, которые называются нормальными. Однако применение нормальных видовых чисел затруднено тем, что каждый раз нужно было устанавливать соотношение и затем уже измерять на этой части высоты диаметр ствола. Кроме того, исследования показали, что нормальные видовые числа изменяются в широких пределах и установить закономерность их изменения также оказалось трудным. Нормальные видовые числа не получили практического применения.

Были предложены постоянные видовые числа для стволов определенной формы, названные абсолютными видовыми числами. При их вычислении площадь сечения ствола на высоте груди принималась за основание, как древесного ствола, так и цилиндра. Высота ствола и цилиндра принимались равными фактической высоте ствола, уменьшенной на 1,3 м. Положительной стороной абсолютных видовых чисел является то, что они не зависят от высоты и остаются постоянными для определенной формы ствола.

Однако абсолютные видовые числа имеют существенный недостаток, так как они не характеризуют частей ствола, расположенных ниже высоты груди. Чем короче ствол, тем большая часть его объема приходится на нижнюю часть. Чтобы устранить этот недостаток, объем части ствола, расположенной ниже высоты груди, определяют отдельно и складывают с кубатурой ствола, находимой с помощью абсолютных видовых чисел. Абсолютные видовые числа также не нашли широкого применения.

В России наибольшее распространение получили старые видовые числа. В результате многочисленных исследований накоплен материал, позволяющий установить средние величины видовых чисел, а также зависимость между ними и диаметрами стволов в разных сечениях.

Для характеристики формы древесных стволов используют также соотношение диаметров ствола, взятых на различной высоте. Отношение любого диаметра ствола к диаметру на высоте груди называется коэффициентом формы.

Для решения таксационных задач чаще всего вычисляют коэффициенты формы по диаметрам у шейки корня (d₀), на одной четверти (d_1/4h), на половине (d_1/2h) и трех четвертях (d_3/4h) высоты ствола. В связи с эти различают четыре коэффициента формы: q₀, q₁, q₂, q₃.

— четвертый коэффициент формы

М.Е. Ткаченко были составлены таблицы всеобщих видовых чисел. Для стволов деревьев всех пород, выросших в насаждении при самых разнообразных условиях и имеющих одинаковый коэффициент формы, с увеличением высоты видовые числа уменьшаются. При одной и той же высоте стволов видовые числа с увеличением коэффициента формы закономерно увеличиваются. Видовые числа зависят от коэффициентов формы больше чем от высоты.

Таблицы имеют недостаток, заключающийся в том, что принятая градация коэффициентов формы 0,05 слишком велика и, следовательно, при пользовании таблицами неизбежна интерполяция, что может привести к ошибкам при их вычислении.

Уточненные и детализированные таблицы всеобщих видовых чисел М.Е. Ткаченко разработаны Г.Б. Кофманом и Б.Е. Поповым. Преимущество таких таблиц заключается в том, что в них принята градация коэффициента формы (q₂) равная 0,025. Поэтому при использовании этих таблиц вероятность интерполяции при вычислении видовых чисел значительно меньше.

Практическое значение видовых чисел и коэффициентов формы заключается главным образом в том, что они являются одним из расчетных элементов, позволяющих составлять объемные таблицы для таксации растущих деревьев.

Источник

Кубатура круглого леса. Как рассчитать объем?

Как правильно рассчитать покупаемый объем древесины для дальнейшей переработки? Если с оцилиндрованным бревном все достаточно просто (уже из названия понятно, что достаточно рассчитать объем цилиндра), то форма необработанного бревна задает нетривиальную задачу при расчетах объема.

Под бревном мы понимаем срубленное дерево, очищенное от веток и крупных сучьев. Форма условного бревна – это цилиндр (в нижней части), переходящий в конус (в верхней части). При этом поперечное сечение дерева очень редко представляет собой круг, а лишь напоминает его очертаниями. Оговоримся сразу, что на практике при расчетах это сечение все-таки принимается за круг без учета погрешностей. Пренебрегают в расчетах и кривизной ствола, измеряя не длину оси, а собственно длину поверхности ствола.

Поэтому для определения объема бревна нам понадобятся те же значения, что и при расчете идеального оцилиндрованного бревна – а именно длина и толщина (диаметр).

Определение объема древесины по таблице

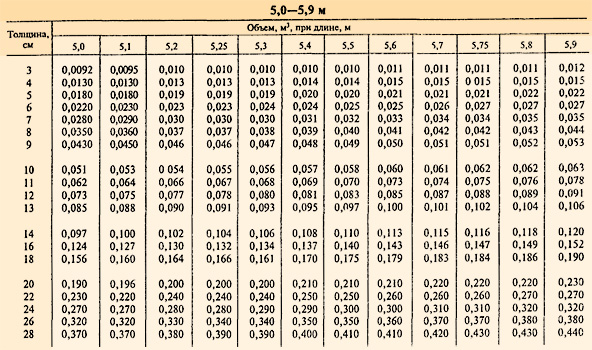
Для быстрого и точного расчёта кубатуры леса можно воспользоваться специальным справочником — кубатурником. Эти таблицы можно найти в ГОСТ 2708-75 и с их помощью быстро определить объём как круглой древесины, так и различных пиломатериалов.

Важно: при определении объема древесины при помощи кубатурников ГОСТа используется наименьший диаметр (т.е. толщина верхнего торца). На каждую из групп длин (от 1 до 1,9 м, от 2 до 2,9 м, от 3 до 3,9 м и т.д.) приводится отельная таблица значений.

Поскольку этот сайт посвящен переработке тонкомерной древесины и оборудованию для распиловки доски из тонкомера, в качестве примера мы показали таблицу определения объема древесины малых диаметров. ГОСТ с кубатурником для других значений можно найти здесь. Сейчас существуют даже специальные мобильные приложения — кубатурники, которые можно найти на Google Play.

Определение объема по формуле

Представим ситуацию, при которой у вас под рукой не оказалось всех этих таблиц и даже нет доступа к интернету (а такое вполне возможно, если вы находитесь на делянке далеко в лесу). В этом случае на помощь придет простая формула расчета площади круга из школьного курса – «пи эр квадрат». Для расчетов нам понадобится замерить диаметр и длину заготовки.

Но как уже было сказано выше – мы имеем дело не с цилиндром и не конусом — бревно представляет собой сочетание этих двух фигур с индивидуальными вариациями кривизны. Значит, будем усреднять значения.

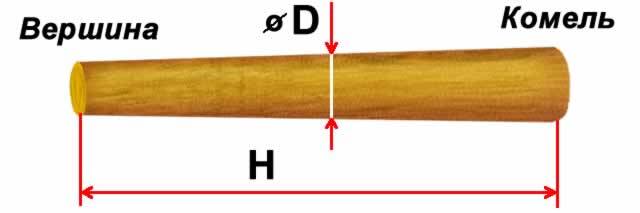
Объем рядового древесного ствола всегда меньше, чем объем условного цилиндра той же высоты и толщины основания (и, к слову, меньше объема конуса с теми же параметрами). Значит, для расчетов объема нам нужно настолько уменьшить диаметр этого условного цилиндра, чтобы он был равен объему бревна со всеми индивидуальными особенностями его формы. Среднее арифметическое между диаметрами верхней и нижней части ствола не всегда дает адекватный результат, поскольку конусность ствола может быть очень неравномерной. Согласно многочисленным исследованиям, диаметром этого условного цилиндра является толщина середины бревна.

Следовательно, для определения объема ствола надо измерить рулеткой его длину рулеткой и диаметр на середине, а затем перемножить эти величины.

Расчет кубатуры большого количества бревен

Поскольку форма и диаметры каждого бревна отличаются, для наиболее точных расчетов правильней всего подсчитать объем каждого бревна и затем сложить все полученные значения. Однако при больших объемах поставок это не всегда возможно да и зачастую не нужно, поскольку погрешность как правило несущественная.

В случае, если необходимо узнать объем достаточно большого количества круглой древесины, лучше воспользоваться другим способом – сделать перерасчет складочного кубического метра в плотный кубический метр. Складочный кубический метр представляет собой количество древесины, которая занимает геометрический объем прямоугольной призмы со сторонами 1 м3 вместе с промежутками.

Чтобы подсчеты были как можно более точными, штабель из бревен должен максимально соответствовать форме призмы, а промежутки между стволами должны быть минимальными. Порядок действий следующий:

• бревна укладываются в штабель, при этом тонкие и толстые концы распределяются в противоположных направлениях;
• короткие фрагменты бревен можно состыковать между собой;
• если заготовки сильно отличаются по длине, то они укладываются в разные штабеля;
• далее остается измерить длину, ширину и высоту каждого штабеля, полученные величины перемножить;
• Сложить показатели объемов каждого из сформированных штабелей.

Итак, мы получили складочную кубатуру леса. Теперь нужно вычислить плотную кубатуру – т.е. собственно объем древесины за вычетом объема пустот между бревнами. Для этого нужно умножить полученную величину объема на расчетный коэффициент.

Коэффициент для расчета плотной кубатуры древесины в штабеле

Вид заготовки

Длина до 2 м

Длина более 2 м

Источник