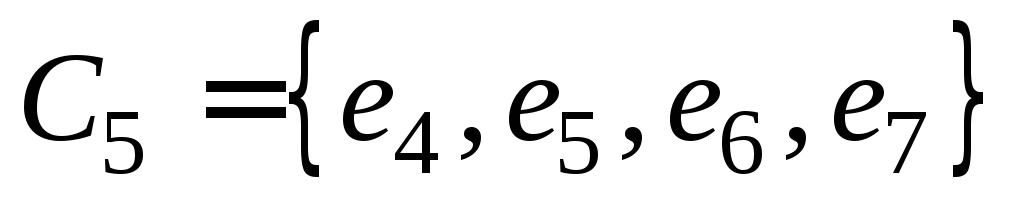4.4. Фундаментальная система циклов. Цикломатическое число
Из определения дерева и теоремы 4.1.1 вытекает следующая теорема.
Теорема 4.4.1. Число ребер произвольного неориентированного графа , которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно , где – число ребер, – число вершин, – число компонент связности графа .
Доказательство. Рассмотрим -ую компоненту связности графа . Пусть содержит вершин и ребер. Тогда остов графа , являясь деревом, содержит ребро, следовательно, для получения остова из компоненты нужно удалить ребер. Суммируя по всем компонентам связности, получим:
Число называется цикломатическим числом или циклическим рангом графа . Число называется коциклическим рангом или корангом графа и равно числу ребер, входящих в любой остов графа .
Следующие два утверждения являются следствиями доказанной теоремы.
Следствие 4.4.1. Неориентируемый граф является лесом тогда и только тогда, когда .
Следствие 4.4.2. Неориентируемый граф имеет единственный цикл тогда и только тогда, когда .
Пусть – неориентированный граф с вершинами, ребрами; – компоненты связности, – остов графа . Остов имеет ребер , которые называются его ветвями. Оставшиеся ребер , не входящие в , называются хордами остова . Согласно пункту 6 теоремы 4.1.1, если к остову добавить произвольную хорду , то в полученном графе найдется ровно один цикл , состоящий из хорды и некоторых ветвей остова. Цикл называется фундаментальным циклом графа относительно хорды остова . Множество всех фундаментальных циклов относительно хорд остова называется фундаментальным множеством циклов графа относительно остова . Ясно, что мощность фундаментального множества циклов равна цикломатическому числу графа .
Обозначим через последовательность всех ребер графа . Фундаментальному циклу соответствует вектор , определенный по правилу:
Тогда фундаментальное множество циклов задается матрицей фундаментальных циклов
Так как каждый фундаментальный цикл содержит ровно одну хорду , то матрица имеет вид:
где – единичная матрица порядка .
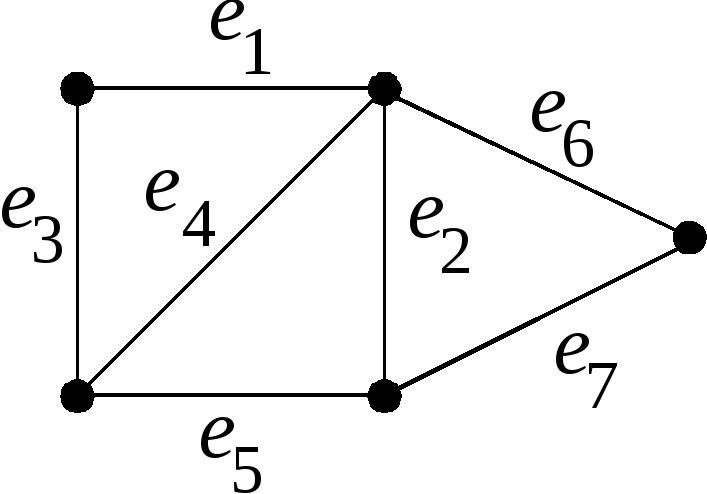
Пример 4.4.1. Найти матрицу фундаментальных циклов графа , изображенного на рисунке 4.4.1.
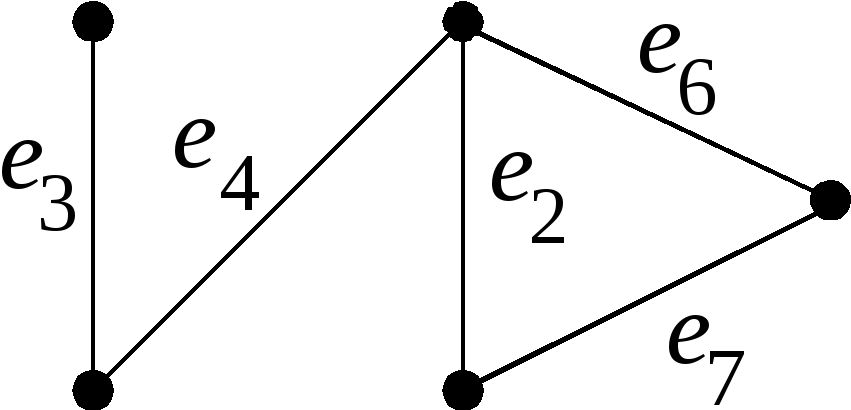
Так как , то для получения остова следует удалить три ребра. Обозначим их номерами Ребра, входящие в остов, обозначим номерами . Фундаментальный цикл , соответствующий хорде , состоит из ребер ; цикл – из ребер ; цикл – из ребер . Поэтому матрица фундаментальных циклов имеет вид:
Выделение фундаментальной системы циклов находит применение при анализе электрических цепей. Если с электрической цепью сопоставить граф, ребра которого соответствуют источникам ЭДС, сопротивлениям, индуктивностям и т.д., а вершины – узлам соединений элементов цепи, то при использовании закона Кирхгофа для напряжений, гласящего, что сумма падения напряжений вдоль цикла равна нулю, необходимо найти фундаментальную систему циклов. Уравнения, отвечающие этим циклам, не будут зависеть друг от друга, в то же время их выполнение будет гарантировать выполнение уравнений для всех циклов графа.
Источник
§ 3.7. Фундаментальная система циклов графа
Абстрактный цикл. Обобщенный цикл. Пространство циклов. Фундаментальная система циклов (базис пространства циклов).
Базовые понятия и утверждения
Пусть 

Это бинарное отношение, будучи отношением эквивалентности, разбивает множество циклов данного графа на классы эквивалентности. Далее в этом параграфе, говоря о циклах графа, будем иметь в виду, если не оговорено противное, классы эквивалентности, а не отдельных их представителей. Эти классы эквивалентности назовем абстрактными циклами. Любой абстрактный циклзадается множеством своих ребер.
Пример 1. Граф, представленный диаграммой на рис. 3.72, имеет следующие абстрактные циклы:


,

Обобщенным цикломбудем называть абстрактный цикл или объединение непересекающихся абстрактных циклов. В число обобщенных циклов включим также цикл без ребер; назовем его пустым циклом и обозначим символом.
На множестве всех обобщенных циклов графа введем две операции:
а) операцию 



(здесь 
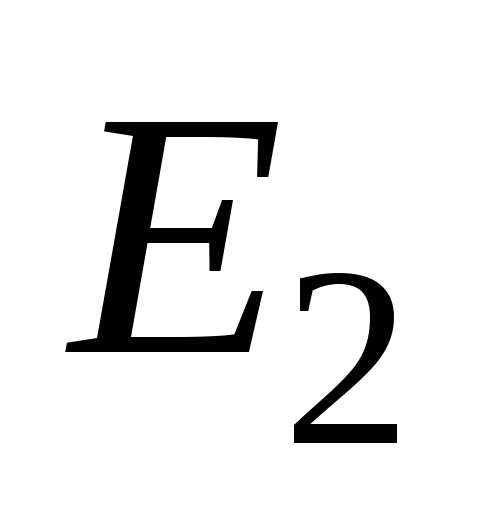


б) операцию умножения на 0 и 1: 

Например, для обобщенных циклов графа из примера 1 имеем:



Множество всех обобщенных циклов графа с операциями сложения по модулю 2 и умножения на 0 и 1 образуют линейное пространство (убедиться в выполнении восьми аксиом линейного пространства несложно).
Операция естественным образом распространяется на любое конечное число обобщенных циклов.
Линейной комбинацией обобщенных циклов


Говорят, что система обобщенных циклов 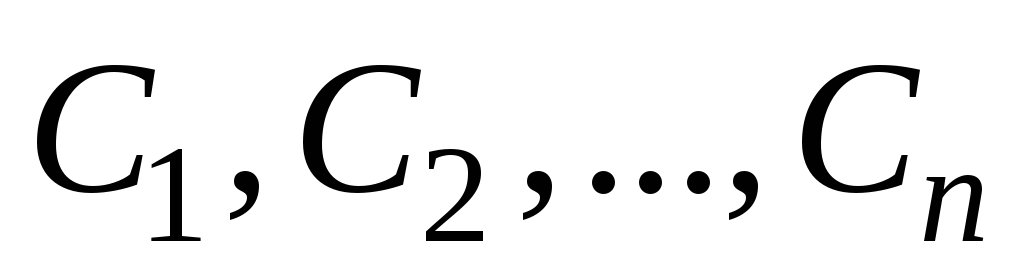



Система обобщенных циклов 

1) линейно независима;
2) любой обобщенный цикл 


Базис линейного пространства циклов называют фундаментальной системой циклов.
Из курса линейной алгебры нам известно, что в линейном пространстве может быть несколько базисов, но все они состоят из одного числа векторов линейного пространства (напомним, что это число называют размерностью линейного пространства).
Представляют интерес два вопроса: 1) из скольких циклов состоит фундаментальная система циклов произвольного графа и 2) как найти фундаментальную систему циклов графа?
Ответ на первый вопрос дает следующее утверждение: число циклов в любой фундаментальной системе циклов графа равно его цикломатическому числу.
Приведем алгоритм построения фундаментальной системы циклов произвольного графа.
1-й шаг.Находим в графе



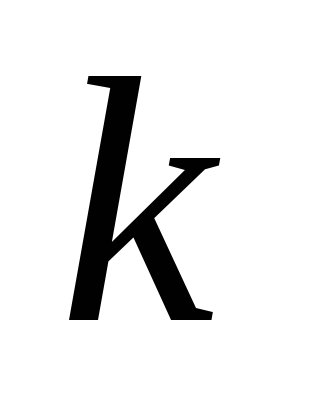
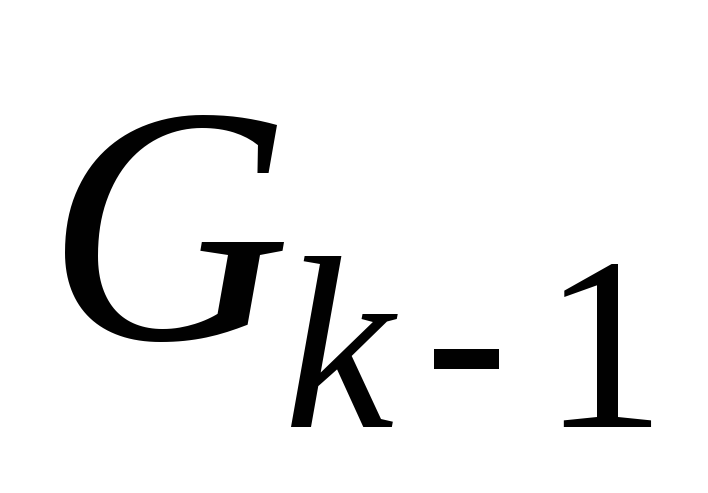




Если в графе 



Пример 2.Построим фундаментальную систему циклов графаиз примера 1.
1-й шаг.Возьмем цикл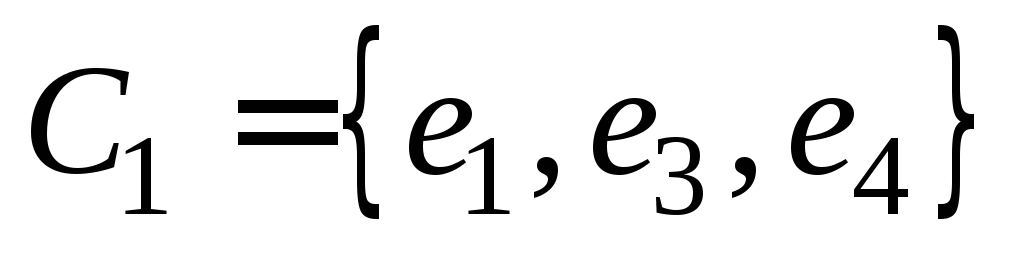

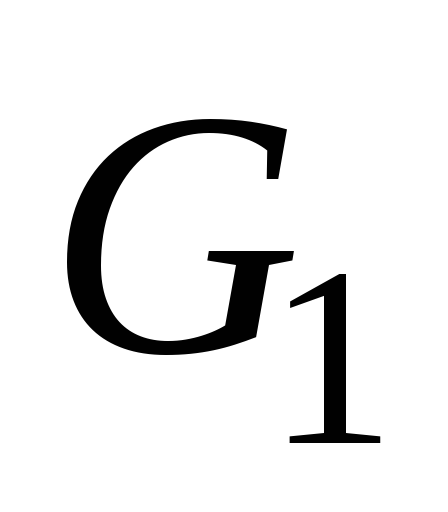
2-й шаг.В графе



3-й шаг.В графе



Следовательно, 


Заметим, что действия по алгоритму не строго детерминированы: на каждом шаге мы имели несколько вариантов выбираемого цикла и удаляемого из него ребра. Если бы наш выбор был иным, то мы нашли бы другую фундаментальную систему циклов. Однако число циклов в этой другой фундаментальной системе тоже было бы равно трем. Например, 

Источник
Пространство циклов графа
Понятие фундаментального цикла вводится следующим образом. Пусть в связном графе G= произвольно фиксировано максимальное остовное дерево Т(V, ET). Рёбра графа G, не принадлежащие дереву Т, называются хордами, а множество хорд T* = E\ET, называется кодеревом графа G, соответствующим дереву Т. Таким образом, каждый максимальный остов однозначно определяет разбиение рёбер графа на подмножества древесных рёбер и хорд.
Алгоритмы поиска в глубину и в ширину строят остовные деревья, причём изменение порядка вершин в списках смежности (и выбор начальной вершины) приводит к построению алгоритмами разных остовных деревьев. Однако, не все деревья удаётся построить с помощью поиска в глубину – см. пример.
Понятие фундаментального цикла позволяет ввести на графах алгебраическую структуру, весьма востребованную в приложениях (законы Кирхгофа, диаграммы Фейнмана). Соответствующий раздел теории графов называется цикломатикой.
По свойству деревьев, добавление любого ребра к дереву приводит к появлению единственного цикла. Поэтому множество хорд данного остова задаёт множество простых циклов, называемых фундаментальными циклами графа. При этом все получающиеся циклы разные. Множество фундаментальных циклов называется фундаментальной системой циклов. Количество циклов в фундаментальной системе называется цикломатическим числом или циклическим рангом графа.
Пусть граф G = имеет n вершин и m рёбер. Если n=m+1, то граф – дерево. Если же n £ m, то в графе есть цикл. После удаления ребра из цикла граф остаётся связным. Если это не дерево, можно снова найти цикл и удалить из него ребро. Продолжая процедуру, приходим в конце концов к некоторому остовному дереву. Количество удалённых рёбер, таким образом, будет в точности равно циклическому рангу графа: C(G) = m – n + 1. Ранг дерева равен 0, графа с одним циклом – 1 и т.д. Изменение порядка удаления рёбер из данного графа приводит, вообще говоря, к разным остовным деревьям, но циклический ранг, очевидно, от этого не зависит.
Во многих задачах требуется перечислить все остовные деревья и выбрать из них оптимальное. В силу установленной однозначной связи остов Þ множество хорд «множество фундаментальных циклов эту задачу можно решать разными способами.
Алгебраический подход. Каждый цикл а = (v(i1), …, v(ik)) в графе однозначно задаёт множество рёбер С(а) Ì Е. Обратно, если некоторое множество рёбер С образует цикл, то по нему можно восстановить последовательность вершин цикла (v(i1), …, v(ik)) – с точностью до выбора начальной вершины и направления обхода. Таким образом, можно отождествить множество циклов графа и семейство подмножеств множества рёбер. Пользуясь этим соответствием, введём на множестве циклов графа структуру векторного пространства.
Определим операцию сложения для циклов:
a + b F C(a) D C(b); 0 F Æ.
Результат операции, вообще говоря, будет не циклом, а дизъюнктивным (несвязным) объединением циклов. Если к операции сложения добавить умножение на число из поля Галуа Z2:
0 a F 0, 1 a F a;
то полученное линейное пространство будет называться пространством циклов.
Линейность пространства позволяет ввести понятия линейной комбинации и линейной независимости и воспользоваться результатами теории векторных пространств. Именно: а) пространство циклов характеризуется определённой размерностью r; б) любой цикл может быть представлен в виде суммы по r базисным векторам. Нетрудно понять, что базисом является любая система фундаментальных циклов, r есть циклическое число графа, а выбор разных остовов есть переход к другому базису в пространстве циклов. Следствием также является утверждение о равенстве числа удалённых хорд циклическому рангу графа C(G) = r.
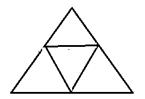
Пример. Граф с 6-ю вершинами имеет 4 фундаментальных цикла, определяемых остовом. Симметрическая разность Z1DZ4 даёт те же 2 цикла, симметрическая разность Z1DZ2DZ3DZ4 – внешнюю границу графа. Симметрическая разность даёт Z1DZ3DZ4 эйлеров цикл данного графа.
Замечание. Четыре естественных треугольника являются базисом пространства циклов, но не являются фундаментальной системой ни для какого остова.
В последующем алгоритме для построения остова используется задание графа списком рёбер. Остов графа G получается в результате «разрастания» леса, являющегося подграфом G.
Алгоритм построения остова для произвольного графа G.
1. Выбрать произвольное ребро, не являющееся петлёй. Пометить его меткой a и объявить (под)деревом это ребро вместе с концевыми вершинами.
2. Выбрать следующее ребро, не являющееся петлёй:
а) если оба конца выбранного ребра принадлежат одному дереву, пометить его меткой b и перейти к шагу 3;
б) если один из концов ребра принадлежит построенному ранее (под)дереву В, а другой конец свободен (не принадлежит ни одному дереву), пометить его меткой a, включить его вместе с концами в дерево В и перейти на метку 3;
в) если концы выбранного ребра принадлежат построенным ранее деревьям В и С, пометить выбранное ребро меткой a, включить его и дерево С в дерево В и перейти к шагу 3;
г) если оба конца ребра свободны, пометить его меткой a, объявить это ребро вместе с вершинами новым деревом в лесу и перейти на 3;
если непомеченных рёбер нет, закончить алгоритм.
3. Если все вершины графа G вошли в одно дерево, закончить алгоритм. Если нет, перейти к шагу 2.
Под словом «выбрать» подразумевается некоторая процедура перечисления рёбер – это может быть случайный выбор, выбор в соответствии с некоторыми приоритетами – например, весом, цветом или стоимостью – так что необходимо использовать некоторую вспомогательную процедуру упорядочивания (сортировки) рёбер.
Замечание. Этот алгоритм, в принципе, может перебрать все остовы.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник