Функция определения глубины дерева

Определить глубину бинарного дерева Delphi

Доброго времени суток.
Есть такая задача:
Описать функцию или пpоцедуpу, котоpая опpеделяет максимальную глубину непустого деpева, т.е. число ветвей в самом длинном из путей от коpня деpева до листьев.

Есть код построения и вывода дерева на экран, а вот определение глубины никак не могу придумать как реализовать.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61

program bin_derevo; uses SysUtils; type int=integer; svd=^zvd; zvd=record key:integer; info:int; left:svd; right:svd; end; var d:svd; k,t:integer; i:int; procedure s_add (k:integer; i:int; var d:svd); begin if d=nil then begin new(d); d^.key:=k; d^.info:=i; d^.left:=nil; d^.right:=nil; end else if k^.key then s_add(k,i,d^.left) else if k>d^.key then s_add(k,i,d^.right); end; procedure print_d(d:svd; l:integer); var i:integer; Begin if d<>nil then begin print_d(d^.right,l+1); for i:=1 to l do write(' '); writeln('* ',d^.key); print_d(d^.left,l+1); end; End; begin writeln('Vvedite chisla razdelaya klavishey enter, dlya zaversheniya vvedite 0'); readln(i); while i<>0 do begin k:=i; s_add(k,i,d); readln(i); end; print_d(d,3); readln; end.

Источник

Деревья. Подсчет глубины (высоты) дерева — C (СИ)

Код к задаче: «Деревья. Подсчет глубины (высоты) дерева»

#include #include #include typedef struct tree < int key; char s[100]; struct tree* left; struct tree* right; >Tree; int Tree_Add(Tree** tr, int key, const char* s); void Tree_Print(FILE* _out, const Tree* tr); void Tree_Clear(Tree* tr); unsigned int Tree_Height(const Tree* tr); int main(void) < Tree* tr = NULL; Tree_Add(&tr, 32, "Pascal"); Tree_Add(&tr, 26, "Algol"); Tree_Add(&tr, 64, "Lisp"); Tree_Add(&tr, 16, "Snobol"); Tree_Add(&tr, 48, "Cobol"); Tree_Print(stdout, tr); printf("height tree: %u\n", Tree_Height(tr)); Tree_Clear(tr); return 0; >//вставка int Tree_Add(Tree** tr, int key, const char* s)< Tree* p = *tr; while(p != NULL)< if(key < p->key)< tr = &p->left; p = p->left; > else if(key > p->key)< tr = &p->right; p = p->right; > else return 0; > p = (Tree*)malloc(sizeof(Tree)); if(p != NULL)< p->left = p->right = NULL; p->key = key; strcpy(p->s, s); *tr = p; > return (p != NULL); > //печать void Tree_Print(FILE* _out, const Tree* tr)< if(tr != NULL)< if(tr->left != NULL) Tree_Print(_out, tr->left); fprintf(_out, "key: %d Value: %s\n", tr->key, tr->s); if(tr->right != NULL) Tree_Print(_out, tr->right); > > //удаление всех void Tree_Clear(Tree* tr)< if(tr != NULL)< if(tr->left != NULL) Tree_Clear(tr->left); if(tr->right != NULL) Tree_Clear(tr->right); free(tr); > > //высота дерева unsigned int Tree_Height(const Tree* tr)< unsigned int l, r; if(tr != NULL)< l = (tr->left != NULL) ? Tree_Height(tr->left) : 0; r = (tr->right != NULL) ? Tree_Height(tr->right) : 0; return ((l > r) ? l : r) + 1; > return 0; >

Источник

1.1. Определение глубины дерева

При определении минимальной (максимальной) длины ветви дерева каждая вершина должна получить значения минимальных длин ветвей от потомков, выбрать из них наименьшую и передать предку результат, увеличив его на 1 — » добавить себя» .

//—- Определение ветви минимальной длины

Для отслеживания процесса » погружения» достаточно дополнительной переменной, которая уменьшает свое значение на 1 при очередном рекурсивном вызове.

//——Включение вершины в дерево на заданную глубину

if (d == 0) return 0; // Ниже не просматривать

if (Insert(ph->p[i], v , d-1)) return 1; // Вершина включена

Для включения простейшим способом нового значения в дерево в ближайшее в корню место достаточно соединить две указанные функции вместе.

1.2. Операции поиска и включения элемента в дерево

При обнаружении в дереве первого значения, удовлетворяющего условию, необходимо прервать не только текущий шаг рекурсии, но и все предыдущие. Поэтому цикл рекурсивного вызова прерывается сразу же, как только потомок возвратит найденное в поддереве значение. Текущая вершина должна » ретранслировать» полученное от потомка значение к собственному предку (» вверх по инстанции» ).

//—- Поиск в дереве строки, длиной больше заданной

if (strlen(q->str)> 5) return q->str; // Найдена в текущей вершине

char *child=big_str(q->p[i]); // Получение строки от потомка

if (child!=NULL) return child; // Вернуть ее » от себя лично»

return NULL;> // Нет ни у себя, ни у потомков

Производится полный обход дерева, в каждой вершине стандартный контекст выбора минимального из текущего значения в вершине и значений, полученных от потомков при рекурсивном вызове функции.

//—- Поиск максимального в дереве

1.3. Оптимизация поиска в дереве

Основное свойство дерева соответствует пословице » дальше в лес — больше дров» . Точнее, количество просматриваемых вершин от уровня к уровню растет в геометрической прогрессии. Если известен некоторый критерий частоты использования различных элементов данных (например, более короткие строки используются чаще, чем длинные), то в соответствии с ним можно частично упорядочить данные по этому критерию с точки зрения их » близости» к корню : в нашем примере в любом поддереве самая короткая строка находится в его корневой вершине. Алгоритм поиска может ограничить глубину просмотра такого дерева.

//— Дерево оптимизацией : короткие ключи ближе к началу

void *data; // Искомая информация

void *find(dtree *q, char *keystr) // Поиск по ключу

if (strcmp(q->key,keystr)==0) return q->data; // Ключ найден

return NULL; // Короткие строки — ближе к корню

if ((s=find(q->p[i],keystr))!=NULL) return s;

Функция включения в такое дерево ради сохранения свойств должна в каждой проходимой ею вершине рекурсивно » вытеснять» более длинную строку в поддерево и заменять ее на текущую (новую), более короткую.

Источник

Реализуем алгоритм поиска в глубину

В этом туториале описан алгоритм поиска в глубину (depth first search, DFS) с псевдокодом и примерами. Кроме того, расписаны способы реализации поиска в глубину в C, Java, Python и C++.

“Поиск в глубину” или “обход в глубину” — это рекурсивный алгоритм по поиску всех вершин графа или дерева. Обход подразумевает под собой посещение всех вершин графа.

Алгоритм поиска в глубину

Стандартная реализация поиска в глубину помещает каждую вершину (узел, node) графа в одну из двух категорий:

Цель алгоритма состоит в том, чтобы пометить каждую вершину как “Пройденная”, избегая при этом циклов.

Алгоритм поиска в глубину работает следующим образом:

1. Начните с того, что поместите любую вершину графа на вершину стека.
2. Возьмите верхний элемент стека и добавьте его в список “Пройденных”.
3. Создайте список смежных вершин для этой вершины. Добавьте те вершины, которых нет в списке “Пройденных”, в верх стека.
4. Необходимо повторять шаги 2 и 3, пока стек не станет пустым.

Пример реализации поиска в глубину

Предлагаю рассмотреть на примере, как работает алгоритм поиска в глубину. Мы будем использовать неориентированный граф с пятью вершинами.

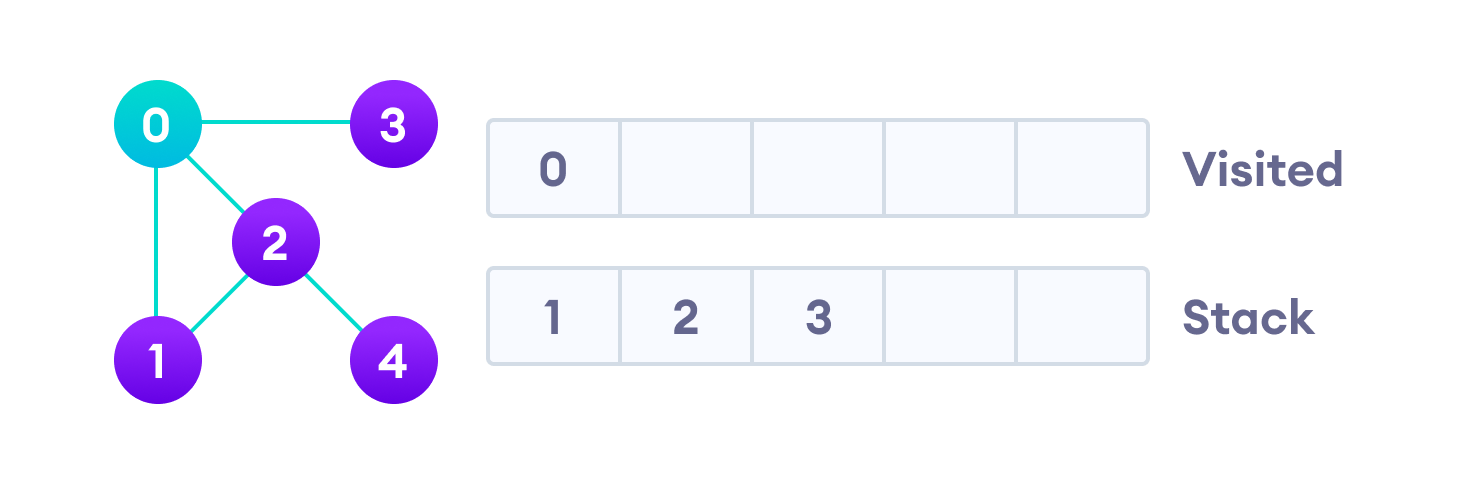
Начнем мы с вершины “0”. В первую очередь алгоритм поиска в глубину поместит ее саму в список “Пройденные” (на изображении “Visited”), а ее смежные вершины — в стек.

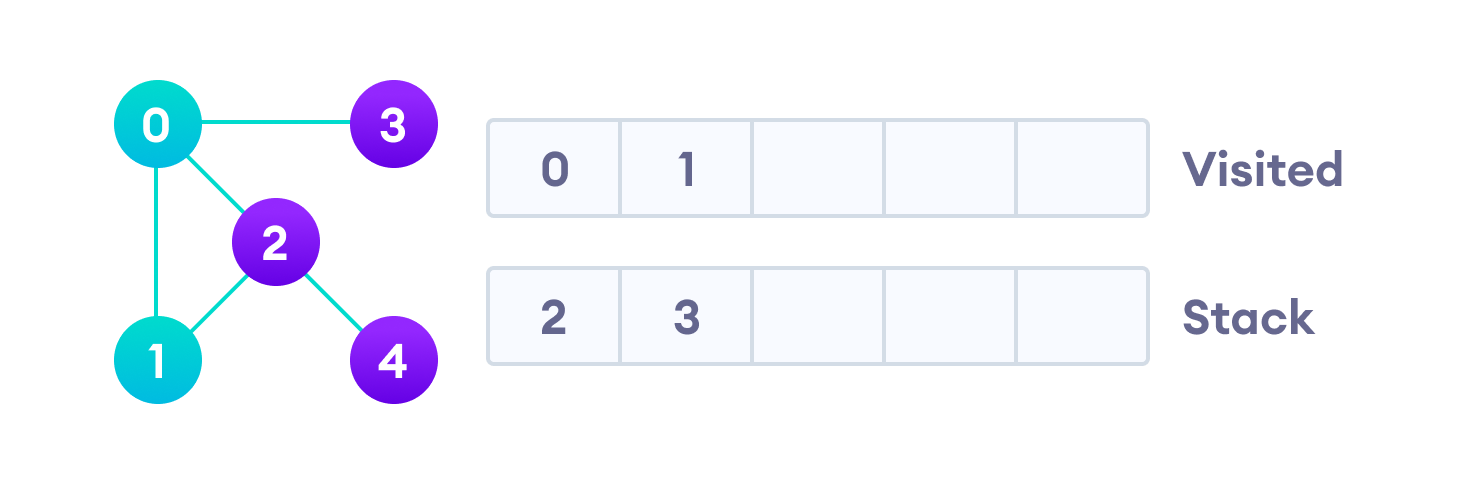
Затем мы берем следующий элемент сверху стека, т.е. к вершину “1”, и переходим к ее соседним вершинам. Поскольку вершина “0” уже пройдена, следующая вершина “2”.

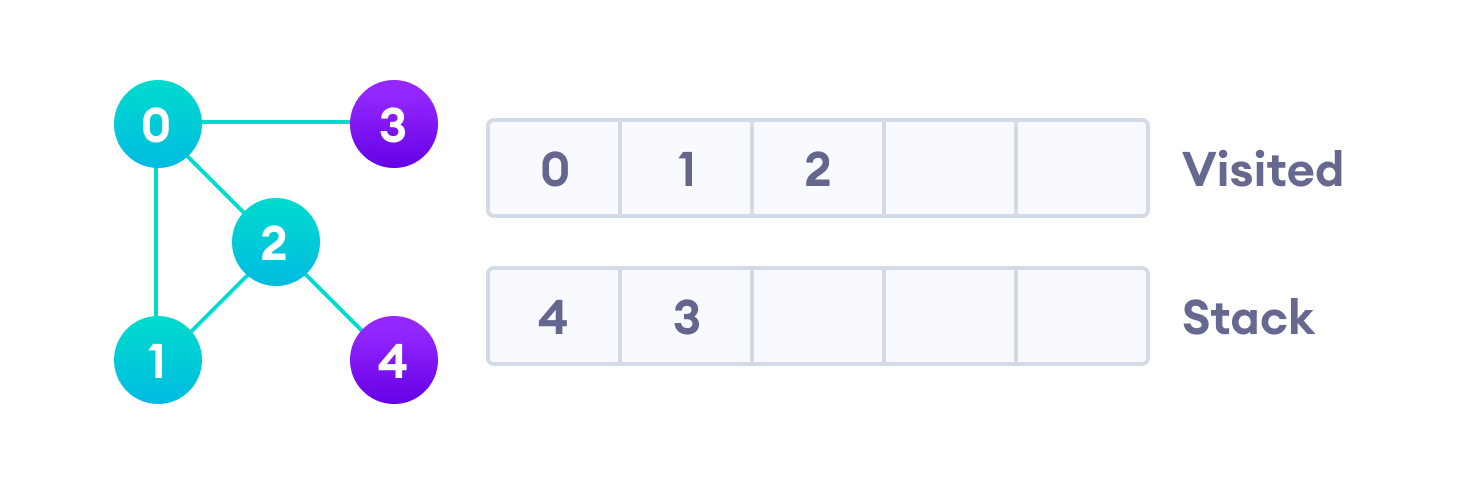
Вершина “2” смежна непройденной вершине “4”, следовательно мы добавляем ее наверх стека и проходим ее.

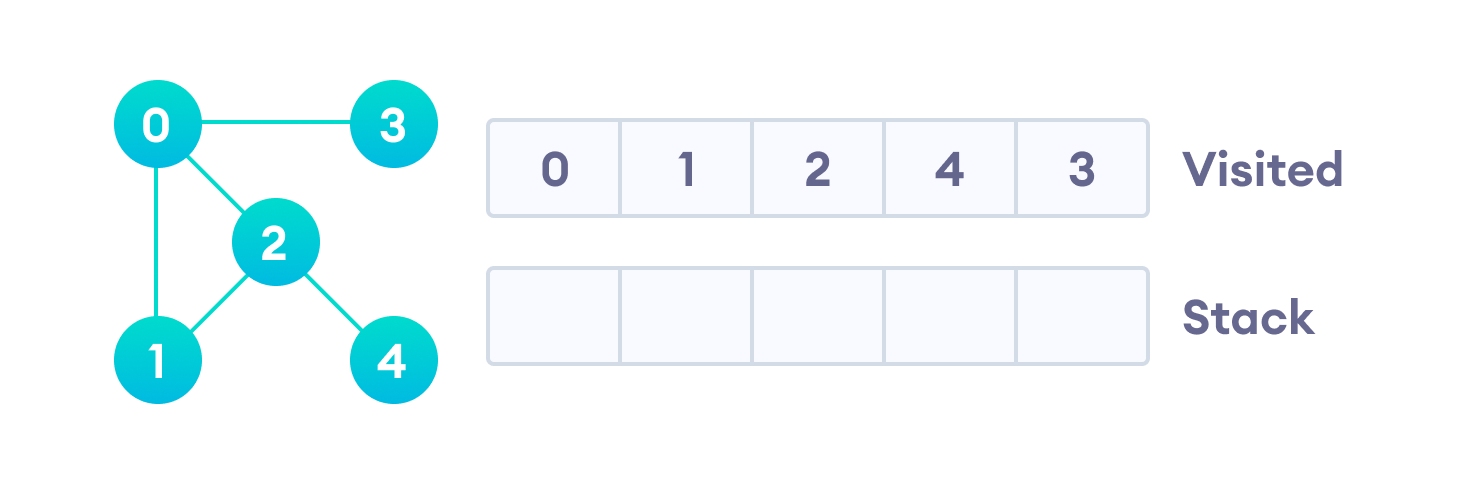
После того, как мы пройдем последний элемент (вершину “3”), в стеке не останется непройденных смежных вершин, и таким образом мы завершили обход графа в глубину.

Псевдокод поиска в глубину (рекурсивная реализация)

Ниже представлен псевдокод для алгоритма поиска в глубину. Обратите внимание, что в функции init() необходимо запускать функцию DFS на каждой вершине. Это связано с тем, что граф может иметь две разные несвязанные части, поэтому для того, чтобы убедиться, что мы покрываем каждую вершину, мы должны запускать алгоритм поиска в глубину на каждой вершине.

DFS(G, u) u.visited = true for each v ∈ G.Adj[u] if v.visited == false DFS(G,v) init()

Реализация поиска в глубину на Python, Java и C/C++

Ниже приведены примеры реально кода алгоритма поиска в глубину. Код был упрощен, чтобы мы могли сфокусироваться на самом алгоритме, а не на других деталях.

# Алгоритм поиска в глубину на Python # Алгоритм def dfs(graph, start, visited=None): if visited is None: visited = set() visited.add(start) print(start) for next in graph[start] - visited: dfs(graph, next, visited) return visited graph = dfs(graph, '0')

// Алгоритм поиска в глубину на Java import java.util.*; class Graph < private LinkedListadjLists[]; private boolean visited[]; // Создание графа Graph(int vertices) < adjLists = new LinkedList[vertices]; visited = new boolean[vertices]; for (int i = 0; i < vertices; i++) adjLists[i] = new LinkedList(); > // Добавление ребер void addEdge(int src, int dest) < adjLists[src].add(dest); >// Алгоритм void DFS(int vertex) < visited[vertex] = true; System.out.print(vertex + " "); Iteratorite = adjLists[vertex].listIterator(); while (ite.hasNext()) < int adj = ite.next(); if (!visited[adj]) DFS(adj); >> public static void main(String args[]) < Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 3); System.out.println("Following is Depth First Traversal"); g.DFS(2); >> 

// Алгоритм поиска в глубину на C #include #include struct node < int vertex; struct node* next; >; struct node* createNode(int v); struct Graph < int numVertices; int* visited; // Нам нужен int** для хранения двумерного массива. // Аналогично, нам нужна структура node** для хранения массива связанных списков. struct node** adjLists; >; // Алгоритм void DFS(struct Graph* graph, int vertex) < struct node* adjList = graph->adjLists[vertex]; struct node* temp = adjList; graph->visited[vertex] = 1; printf("Visited %d \n", vertex); while (temp != NULL) < int connectedVertex = temp->vertex; if (graph->visited[connectedVertex] == 0) < DFS(graph, connectedVertex); >temp = temp->next; > > // Создание вершины struct node* createNode(int v) < struct node* newNode = malloc(sizeof(struct node)); newNode->vertex = v; newNode->next = NULL; return newNode; > // Создание графа struct Graph* createGraph(int vertices) < struct Graph* graph = malloc(sizeof(struct Graph)); graph->numVertices = vertices; graph->adjLists = malloc(vertices * sizeof(struct node*)); graph->visited = malloc(vertices * sizeof(int)); int i; for (i = 0; i < vertices; i++) < graph->adjLists[i] = NULL; graph->visited[i] = 0; > return graph; > // Добавление ребра void addEdge(struct Graph* graph, int src, int dest) < // Проводим ребро от начальной вершины ребра графа к конечной вершине ребра графа struct node* newNode = createNode(dest); newNode->next = graph->adjLists[src]; graph->adjLists[src] = newNode; // Проводим ребро из конечной вершины ребра графа в начальную вершину ребра графа newNode = createNode(src); newNode->next = graph->adjLists[dest]; graph->adjLists[dest] = newNode; > // Выводим граф void printGraph(struct Graph* graph) < int v; for (v = 0; v < graph->numVertices; v++) < struct node* temp = graph->adjLists[v]; printf("\n Adjacency list of vertex %d\n ", v); while (temp) < printf("%d ->", temp->vertex); temp = temp->next; > printf("\n"); > > int main()

// Алгоритм прохода в глубину в C++ #include #include using namespace std; class Graph < int numVertices; list*adjLists; bool *visited; public: Graph(int V); void addEdge(int src, int dest); void DFS(int vertex); >; // Инициализация графа Graph::Graph(int vertices) < numVertices = vertices; adjLists = new list[vertices]; visited = new bool[vertices]; > // Добавление ребер void Graph::addEdge(int src, int dest) < adjLists[src].push_front(dest); >// Алгоритм void Graph::DFS(int vertex) < visited[vertex] = true; listadjList = adjLists[vertex]; cout << vertex << " "; list::iterator i; for (i = adjList.begin(); i != adjList.end(); ++i) if (!visited[*i]) DFS(*i); > int main()

Сложность алгоритма поиска в глубину

Временная сложность алгоритма поиска в глубину представлена ​​в виде O(V + E), где V — количество вершин, а E — количество ребер.

Пространственная сложность алгоритма равна O(V).

Применения алгоритма

1. Для поиска пути.
2. Для проверки двудольности графа.
3. Для поиска сильно связанных компонентов графа.
4. Для обнаружения циклов в графе.

Приглашаем всех желающих на открытый урок в OTUS «Теория графов. Термины и определения. Основные алгоритмы», регистрация доступна по ссылке.

Источник