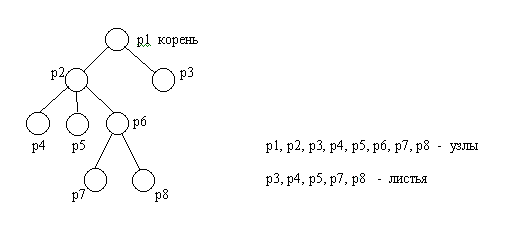Граф дерево бинарное дерево

Графы и деревья

Поскольку любое дерево является графом , то его можно задавать любым из способов, перечисленных в п. «Способы представления графов «. Однако существуют и специальные способы представления, предназначенные только для деревьев . Мы рассмотрим только два наиболее распространенных частных случая.

Представление корневого дерева

Этот способ подходит только для тех корневых деревьев , у которых точно известно максимальное количество потомков для любой вершины .

type ukazatel = ^tree; tree = record znachenie : integer; siblings : array[1..S] of ukazatel; end;

Разумеется, в общем случае значение переменной S (количество потомков ) может достигать N-1 ( N — количество всех вершин в дереве ). Однако ясно, что в такой ситуации особого смысла в динамической древесной структуре нет: экономии памяти не получается. Гораздо лучше, если у всех вершин примерно одинаковое и заранее известное количество потомков .

Представление бинарного дерева

Разновидностью описанного выше частного случая является бинарное корневое дерево : каждая его вершина имеет не более двух потомков :

type ukazatel = ^tree; tree = record znachenie : integer; left_sibling : ukazatel; right_sibling: ukazatel; end;

Примеры использования деревьев

Здесь мы ограничимся только примерами использования бинарных корневых деревьев : именно такой вид графа чаще всего применяется в программировании.

Дерево двоичного поиска

Дерево двоичного поиска для множества чисел S — это размеченное бинарное дерево , каждой вершине которого сопоставлено число из множества S , причем все пометки удовлетворяют следующим условиям:

1. существует ровно одна вершина , помеченная любым числом из множества S ;
2. все пометки левого поддерева строго меньше, чем пометка текущей вершины ;
3. все пометки правого поддерева строго больше, чем пометка текущей вершины .

Если выражаться простым языком, то структура дерева двоичного поиска подчиняется простому правилу: «если больше — направо, если меньше — налево».

Например, для набора чисел 7 , 3 , 5 , 2 , 8 , 1 , 6 , 10 , 9 , 4 , 11 получится такое дерево (см. рис. 11.14).

Для того чтобы правильно учесть повторения чисел, можно ввести дополнительное поле, которое будет хранить количество вхождений для каждого числа.

Более подробно процессы построения и анализа дерева бинарного поиска будут изложены в следующей лекции, посвященной алгоритмам, использующим деревья и графы .

Дерево частотного словаря

Дерево частотного словаря — это результат построения дерева двоичного поиска не для чисел, а для слов некоторого текста. Генерирование дерева частотного словаря полезно при подсчете количества вхождений каждого слова в некоторый текст.

Приведем описание структуры этого дерева :

type ukazatel = ^tree; derevo = record slovo : string[20]; kolichestvo : integer; levyj : ukazatel; pravyj: ukazatel; end;

Дерево синтаксического анализа

Дерево синтаксического анализа арифметического выражения — это бинарное дерево , листьями которого служат операнды, а остальными вершинами — операции, причем уровень вершины соответствует приоритету выполнения операции: чем ближе к листьям , тем приоритет выше.

Например, на рис. 11.15 изображено дерево синтаксического анализа для выражения ((a / (b + c)) + (x * (y — z))) .

Деревья синтаксического разбора строятся компиляторами во время синтаксического анализа программ. Помимо арифметических выражений, которые являются простейшим случаем, аналогичные, но более сложные деревья строятся для всех грамматических конструкций компилируемой программы.

Источник

4. Представление графов и деревьев

Теория графов является важной частью вычислительной математики. С помощью этой теории решаются большое количество задач из различных областей. Граф состоит из множества вершин и множества ребер, которые соединяют между собой вершины. С точки зрения теории графов не имеет значения, какой смысл вкладывается в вершины и ребра. Вершинами могут быть населенными пункты, а ребрами дороги, соединяющие их, или вершинами являться подпрограммы, соединенные вершин ребрами означает взаимодействие подпрограмм. Часто имеет значение направления дуги в графе. Если ребро имеет направление, оно называется дугой, а граф с ориентированными ребрами называется орграфом.

Дадим теперь более формально основное определение теории графов. Граф G есть упорядоченная пара (V,E), где V — непустое множество вершин, E — множество пар элементов множества V, пара элементов из V называется ребром. Упорядоченная пара элементов из V называется дугой. Если все пары в Е — упорядочены, то граф называется ориентированным.

Путь — это любая последовательность вершин орграфа такая, что в этой последовательности вершина b может следовать за вершиной a, только если существует дуга, следующая из а в b. Аналогично можно определить путь, состоящий из дуг. Путь начинающийся в одной вершине и заканчивающийся в одной вершине называется циклом. Граф в котором отсутствуют циклы, называется ациклическим.

Важным частным случаем графа является дерево. Деревом называется орграф для которого :

1. Существует узел, в которой не входит не одной дуги. Этот узел называется корнем.

2. В каждую вершину, кроме корня, входит одна дуга.

С точки зрения представления в памяти важно различать два типа деревьев: бинарные и сильноветвящиеся.

В бинарном дереве из каждой вершины выходит не более двух дуг. В сильноветвящемся дереве количество дуг может быть произвольным.

4.1. Бинарные деревья

Бинарные деревья классифицируются по нескольким признакам. Введем понятия степени узла и степени дерева. Степенью узла в дереве называется количество дуг, которое из него выходит. Степень дерева равна максимальной степени узла, входящего в дерево. Исходя из определения степени понятно, что степень узла бинарного дерева не превышает числа два. При этом листьями в дереве являются вершины, имеющие степень ноль.

Другим важным признаком структурной классификации бинарных деревьев является строгость бинарного дерева. Строго бинарное дерево состоит только из узлов, имеющих степень два или степень ноль. Нестрого бинарное дерево содержит узлы со степенью равной одному.

Рис.4.2. Полное и неполное бинарные деревья

Рис.4.3. Строго и не строго бинарные деревья

4.2. Представление бинарных деревьев

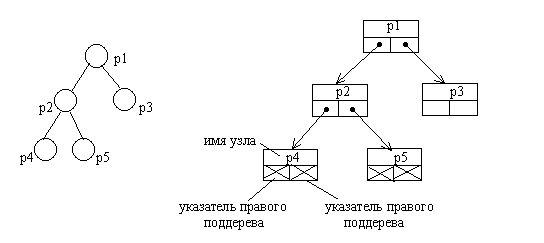
Бинарные деревья достаточно просто могут быть представлены в виде списков или массивов. Списочное представление бинарных деревьев основано на элементах, соответствующих узлам дерева. Каждый элемент имеет поле данных и два поля указателей. Один указатель используется для связывания элемента с правым потомком, а другой — с левым. Листья имеют пустые указатели потомков. При таком способе представления дерева обязательно следует сохранять указатель на узел, являющийся корнем дерева.

Можно заметить, что такой способ представления имеет сходство с простыми линейными списками. И это сходство не случайно. На самом деле рассмотренный способ представления бинарного дерева является разновидностью мультисписка, образованного комбинацией множества линейных списков. Каждый линейный список объединяет узлы, входящие в путь от корня дерева к одному из листьев.

Рис.4.4. Представление бинарного дерева в виде списковой структуры

Приведем пример программы, которая осуществляет создание и редактирование бинарного дерева, представленного в виде списковой структуры

Источник

Граф дерево бинарное дерево

Поиск значения в BST занимает O(log n) времени. Это означает, что можно очень быстро найти требуемое значение среди миллионов или даже миллиардов записей.

Предположим, мы ищем узел со значением x. Чтобы быстро найти его в BST, воспользуемся следующим алгоритмом:

1. Начать с корня дерева.
2. Если x = значению узла: остановиться.
3. Если x < значения узла: перейти к левому дочернему узлу.
4. Если x > значения узла: перейти к правому дочернему узлу.
5. Перейти к шагу 2.

При отсутствии уверенности в существовании искомого узла, необходимо изменить шаги 3 и 4 для остановки поиска.

Если хочешь подтянуть свои знания по алгоритмам, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:

• углубишься в теорию структур данных;
• научишься решать сложные алгоритмические задачи;
• научишься применять алгоритмы и структуры данных при разработке программ.

Реализация

Создание узла TreeNode идентично созданию узла ListNode . Единственное отличие в том, что вместо одного атрибута у нас два: left и right , которые ссылаются на левые и правые дочерние узлы.

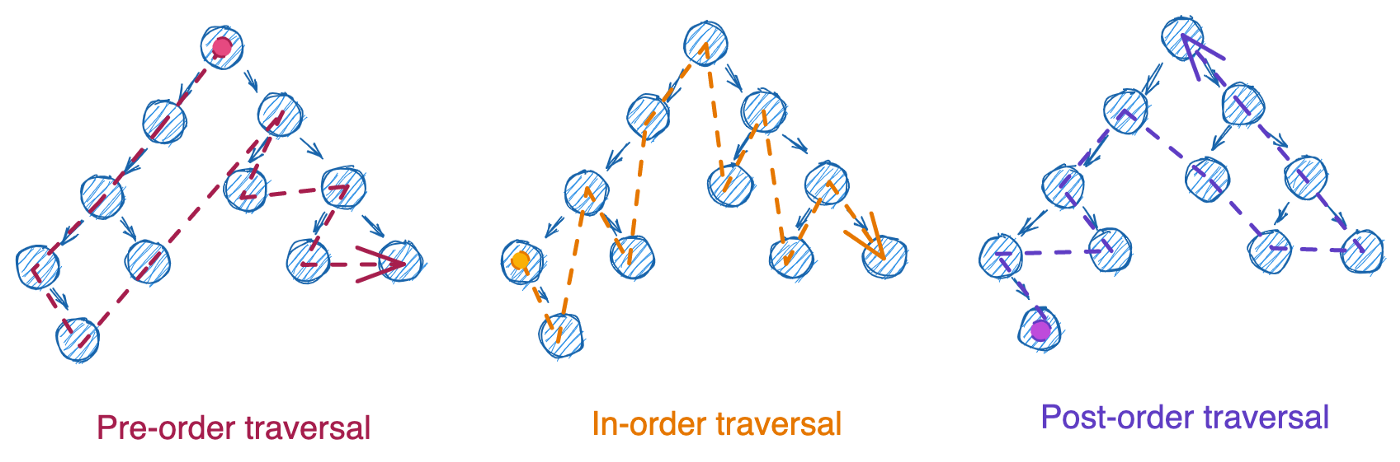
Эти три типа обхода могут быть реализованы следующими методами:

• с итерацией – использование цикла while и стека. В этом случае удаление данных возможно только с конца.
• с рекурсией – использование функции, которая вызывает сама себя.

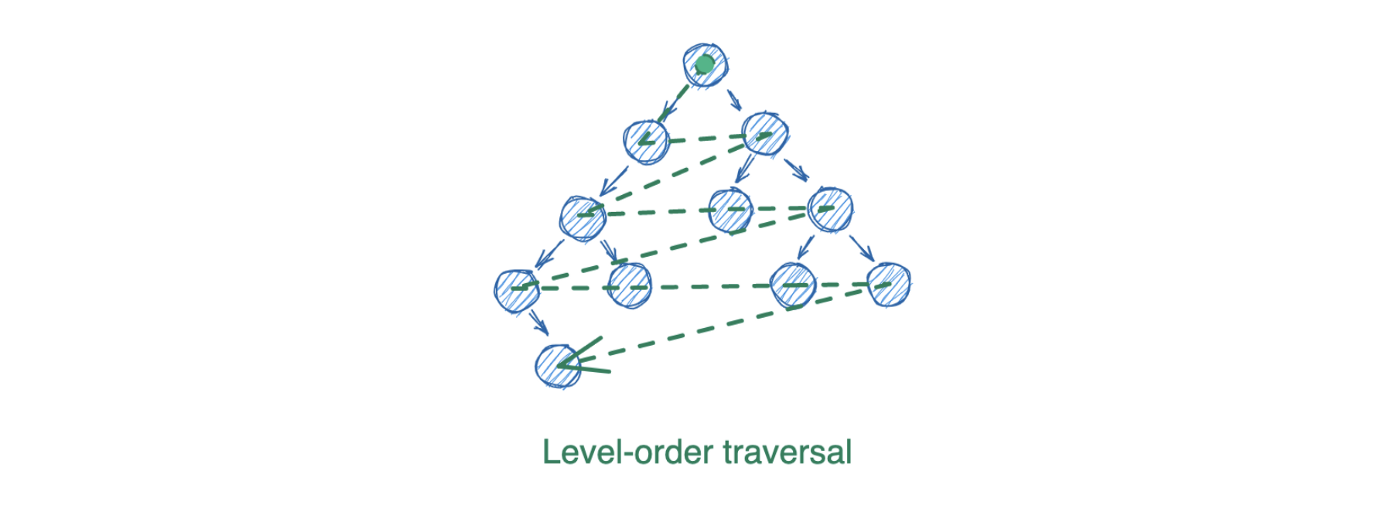
Есть четвертый тип обхода – порядок уровней (level-order traversal). Этот способ использует очередь (queue). Удаление данных здесь возможно только с начала.

Для первых трех типов обработки узлов паттерны практически идентичны. Просто выберем обход в порядке возрастания. Ниже разберем итеративный и рекурсивный методы для LC 94: Binary Tree Inorder Traversal, начиная с итеративной версии:

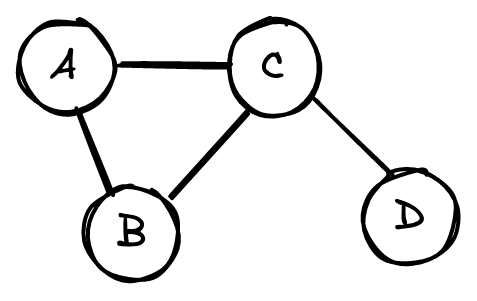
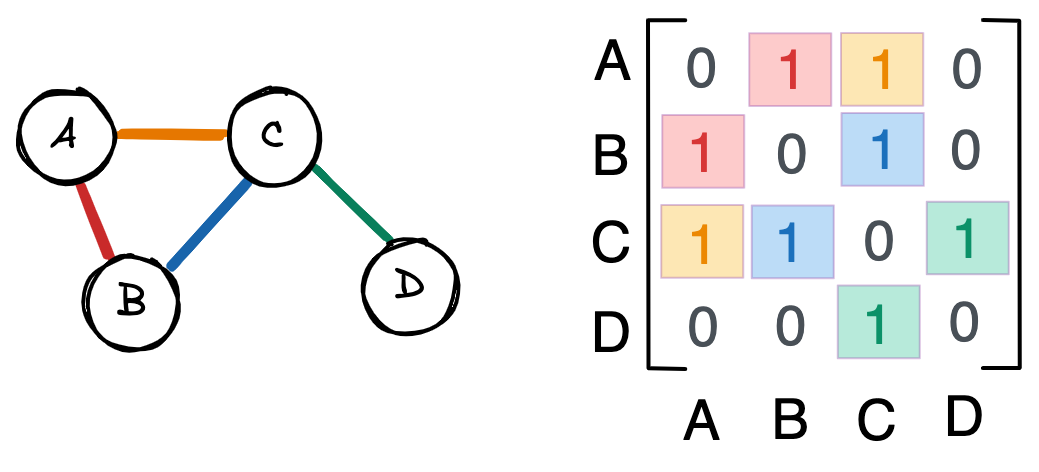
Как правило, графы представлены в виде матриц смежности (adjacency matrix). Так, у приведенного выше графа будет следующая матрица.

Каждая строка и столбец представляют собой узел. Единица в строке i и столбце j , или A_=1 , означает связь между узлом i и узлом j .

A_=0 означает, что узлы i и j не связаны.

Ни один из узлов в этом графе не связан с самим собой. Следовательно, диагональ матрицы равна нулю. Аналогично, A_ = A_ , потому что связи ненаправленны. То есть если узел A связан с узлом B , то B связан с A . В результате матрица смежности симметрична по диагонали.

Рассмотрим пример, который поможет нам понять описанную выше теорию.

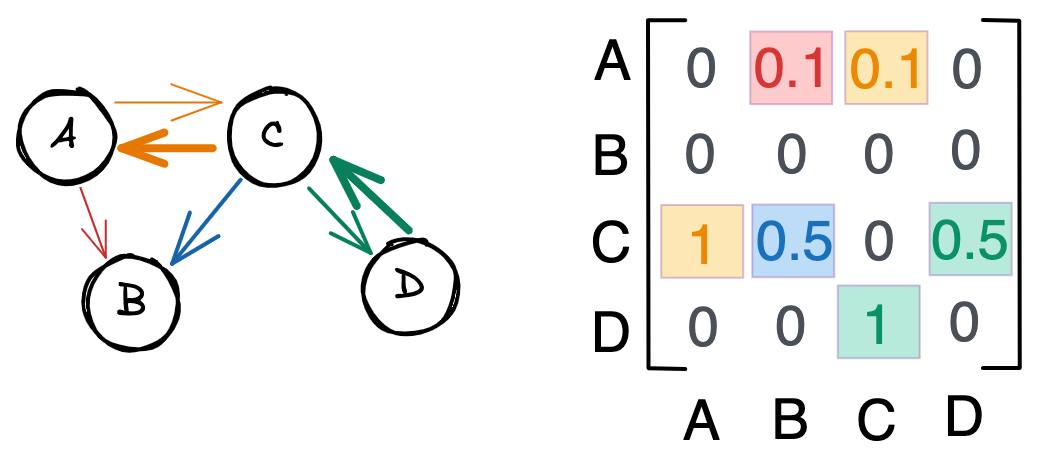
На представленных рисунках мы видим взвешенный граф с направленными ребрами. Обратите внимание, что связи больше не симметричны – вторая строка матрицы смежности пуста, потому что у B нет исходящих связей. Числа от 0 до 1 отражают силу связи. Например, граф C влияет на граф A сильнее, чем A на C .

Реализация

Реализуем невзвешенный и неориентированный граф. Основной структурой класса является список списков Python. Каждый из них – это строка. Индексы в списке представляют собой столбцы. При создании объекта Graph необходимо указать количество узлов n, чтобы создать список списков. Затем мы можем получить доступ к соединению между узлами a и b с помощью self.graph[a][b] .

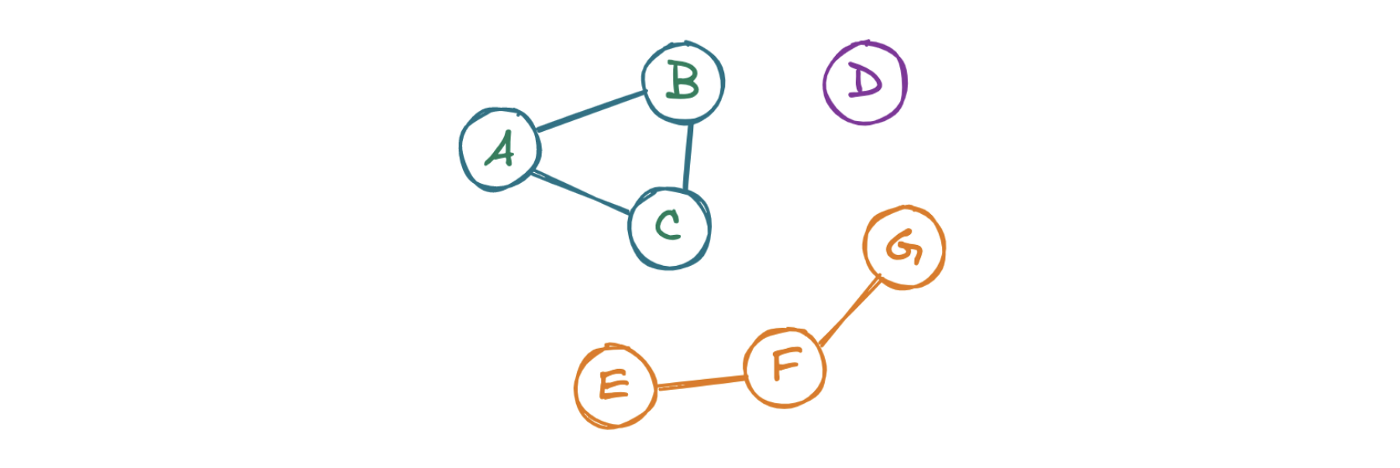
Чтобы ответить на вопрос LC 323: Количество связных компонентов, изучим каждый узел графа. Далее «посетим» соседние графы. Повторяем операцию до тех пор, пока не встретим только те узлы, которые уже были замечены программой. После этого проверим наличие в графе узлов, которые еще не были замечены. Если такие узлы присутствуют, то существует еще как минимум один кластер, поэтому нужно взять новый узел и повторить процесс.

def get_n_components(self, mat: List[List[int]]) -> int: """ Учитывая матрицу смежности, возвращает количество связанных компонентов """ q = [] unseen = [*range(len(mat))] answer = 0 while q or unseen: # Если все соседние узлы прошли через цикл, переходим к новому кластеру if not q: q.append(unseen.pop(0)) answer += 1 # Выбираем узел из текущего кластера focal = q.pop(0) i = 0 # Поиск связей во всех оставшихся узлах while i < len(unseen): node = unseen[i] # Если узел подключен к центру, добавляем его в очередь # чтобы перебрать его соседей # из невидимых узлов и избежать бесконечного цикла if mat[focal][node] == 1: q.append(node) unseen.remove(node) else: i += 1 return answer

1. Строки 5-8: Создаем очередь ( q ), список узлов ( unseen ) и количество компонентов ( answer ).
2. Строка 10: Запускаем цикл while , который выполняем до тех пор, пока в очереди есть узлы, которые нужно обработать или узлы, которые не были замечены.
3. Строки 13-15: Если очередь пуста, удаляем первый узел из непросмотренных и увеличиваем количество компонентов.
4. Строки 18-19: Выбираем следующий доступный узел в очереди ( focal ).
5. Строка 22: Запускаем цикл while , который выполняем до тех пор, пока не обработаем все оставшиеся узлы.
6. Строка 23: Даем имя текущему узлу для оптимизации кода.
7. Строки 28-30: Если текущий узел подключен к центру, добавляем его в очередь узлов текущего кластера. Удаляем его из списка тех узлов, которые могут находиться в невидимом кластере. Благодаря этому действию, мы избегаем бесконечного цикла.
8. Строки 31-32: Если текущий узел не подключен к focal (центру), переходим к следующему узлу.

Заключение

Графы и деревья – основные структуры данных. Спектр их применения огромен. Например, графы используются там, где необходим алгоритм поиска решений. Реальный пример их использования – sea-of-nodes JIT-компилятора.

Деревья используются тогда, когда мы должны произвести быстрое добавление/удаление объекта с поиском по ключу. Например, в различных словарях и индексах БД (Баз данных). Кроме того, деревья являются неотъемлемой частью случайного леса – алгоритма машинного обучения.

В следующей части материала мы приступим к изучению хэш-таблиц.

Базовый и продвинутый курс «Алгоритмы и структуры данных» включает в себя:

1. Живые вебинары 2 раза в неделю.
2. 47 видеолекций и 150 практических заданий.
3. Консультации с преподавателями курса.

Материалы по теме

Источник