Примеры решений задач по теории графов
На этой странице вы найдете готовые примеры по теории графов (разделу дискретной математики). Теория графов берет свое начало еще в 18 веке, когда Эйлер написал свою знаменитую статью о Кёнигсберских мостах (см. решения на алгоритм Эйлера). Сейчас достижения теории графов применяются в строительстве, программировании, электротехнике, социологии, экономике, биохимии, телекоммуникациях и планировании транспортных коммуникаций, психологии и т.д.
Какие виды заданий решаются студентами?
Задачи, решаемые в рамках теории графов, можно условно поделить на несколько групп:
- Определение графа и его свойства. Задачи на построение графа по заданному числу вершин и ребер, построение матрицы смежности и инцидентности, вычисление основных характеристик графа (связность, простота, эйлеровость, полнота, двудольность, регулярность графа и т.п.). Проверка планарности и изоморфности графов.
- Действия с графами. Добавление и удаление вершин и ребер, компонент связности, слияние вершин, объединение, пересечение, соединение и декартово произведение графов. Построение дополнение графа.
- Маршруты, цепи и циклы, контуры. Эйлерова цепь и гамильтонов цикл и проверка графа на выполнение этих свойств.
- Вычисление характеристик графа. Расстояния: диаметр графа, центр графа, радиус графа. Вычисление цикломатического и хроматического числа.
- Задачи на графах. Задача о кратчайшем пути (алгоритм Дейкстры, Беллмана, построение дерева путей). Задача на построение минимального остовного дерева (алгоритм Краскала). Задача о максимальном потоке в сети (алгоритм Форда-Фолкерсона). Задача о раскраске графа.
- Изучение деревьев (специальных видов графов без циклов). Деревья применяются в шифровании, программировании и многих других прикладных областях.
Задачи по графам с решением онлайн
Задача 1. Постройте граф отношения «x+y ≤7» на множестве М=. Определите его свойства.
Задача 2. Найти кратчайшие пути в орграфе от первой вершины ко всем остальным, используя алгоритм Дейкстры. Постройте дерево кратчайших путей.
Задача 3. Найти максимальный поток и минимальный разрез в транспортной сети, используя алгоритм Форда–Фалкерсона (алгоритм расстановки пометок) Построить граф приращений. Проверить выполнение условия максимальности построенного полного потока. Источник – вершина 1, сток – вершина 8.
Задача 4. Постройте остовное дерево минимального веса, используя алгоритмы Прима и Краскала. С помощью матрицы Кирхгоффа найдите количество (неизоморфных) остовных деревьев, используя пакеты компьютерной математики (например, MathCAD, Mathematica, MatLab).
Задача 5. Требуется составить структурную матрицу для данного орграфа (или графа) и, методами булевой алгебры, найти все пути $P_$ из вершины $i$ в вершину $j$, затем найти все сечения $S_$ между этими вершинами. В данном задании (чтобы исключить возможные неясности графического рисунка) указываются все ориентированные ребра, причем запись (2–4) означает, что 2 вершина связана с 4-й, а обратной связи нет. Напомним, что для нахождения путей из вершины $i$ в вершину $j$ нужно раскрывать минор структурной матрицы$М_$ (вычеркивать из структурной матрицы строчку с номером $j$ и столбец с номером $i$). Сечения же находятся отрицанием путей (конъюнкция меняется на дизъюнкцию и наоборот).
Задача 6. Для графа $G=(X,U)$ выполнить следующее:
1.1. Построить:
— матрицу смежности,
— матрицу инцидентности.
1.2. Определить степени для всех вершин $$ данного графа.
Задача 7. Найти все кратчайшие пути в орграфе, используя алгоритм Флойда.
Задача 8. Задан $G (X,ГX)$
$X=$,
ГХ:
Гx1=, Гx2=, Гx3=, Гx4=, Гx5=.
Определить хроматическое и цикломатическое число данного графа.
Задача 9. Считая данный граф неориентированным, обозначить его вершины и рёбра разными символами и определить.
3.1. Локальные степени и окружения каждой вершины в виде структуры смежности;
3.2. Построить матрицы инцидентности и смежности;
3.3. Рассмотреть части графа. Привести примеры суграфа, накрывающего суграфа. Показать подграф, состоящий из трёх вершин. Сколько таких подграфов можно найти в данном графе? Показать примеры пересечения и объединения частей графа;
3.4. Привести примеры циклического маршрута, цепи, простой цепи. Попытаться найти Эйлеров цикл;
3.5. Определить центр, диаметр и радиус графа.
Считая граф ориентированным, определить
3.6. Степени вершин
3.7. Матрицы инцидентности и смежности.
3.8. Привести примеры пути, ориентированной цепи, простой цепи, контура, цикла и простого цикла.
Решение теории графов на заказ
Выполняем решение задач, контрольных и практических работ по любым разделам теории графов. Подробное оформление, таблицы, чертежи, пояснение, возможно написание программ на языках программирования (для алгоритмов на графах) или использование специальных программ. Решение экономических задач, связанных с теорией графов.
Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней. Также оказываем помощь в сдаче тестов по графам.
Источник
Решение задач с помощью графа
Мне нравится Проект нравится 23 участникам
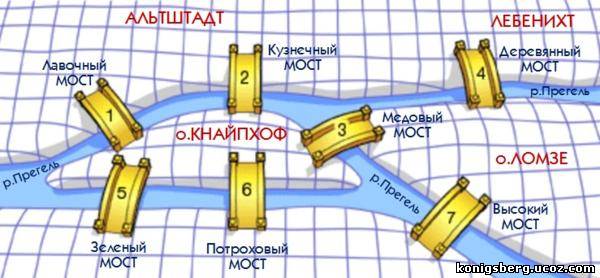
1736 год, г.Кёнигсберг. Через город протекает река Прегеля. В городе — семь мостов, расположенных так, как показано на рисунке выше. С давних времен жители Кенигсберга бились над загадкой: можно ли пройти по всем мостам, пройдя по каждому только один раз? Эту задачу решали и теоретически, на бумаге, и на практике, на прогулках — проходя по этим самым мостам. Никому не удавалось доказать, что это неосуществимо, но и совершить такую «загадочную» прогулку по мостам никто не мог.
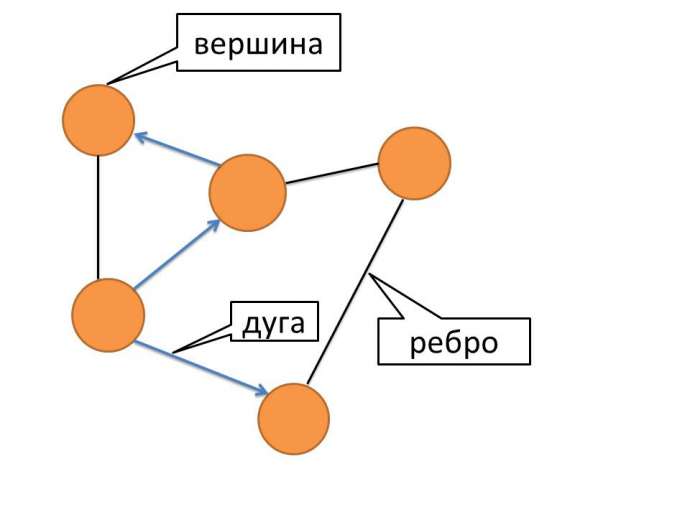
Разрешить проблему удалось знаменитому математику Леонарду Эйлеру. Причем, он решил не только эту конкретную задачу, но придумал общий метод решения подобных задач. При решении задачи о Кенигсбергских мостах Эйлер поступил следующим образом: он «сжал» сушу в точки, а мосты «вытянул» в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют ГРАФОМ.
Граф – это совокупность непустого множества вершин и связей между вершинами. Кружки называются вершинами графа, линии со стрелками – дугами, без стрелок – ребрами.
Виды графов:
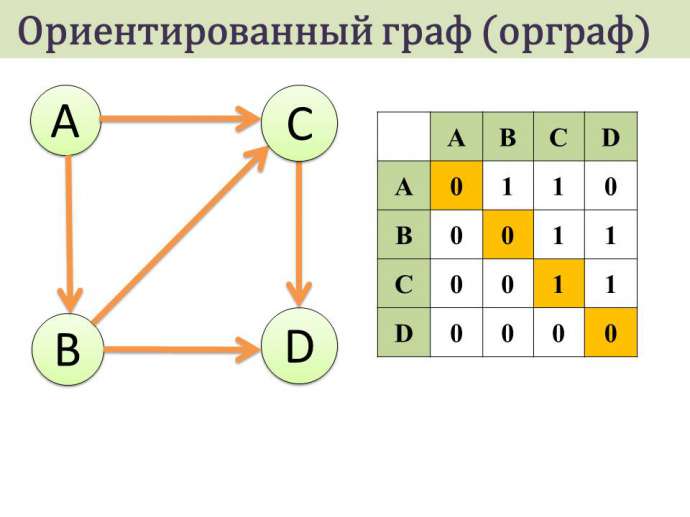
1. Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.
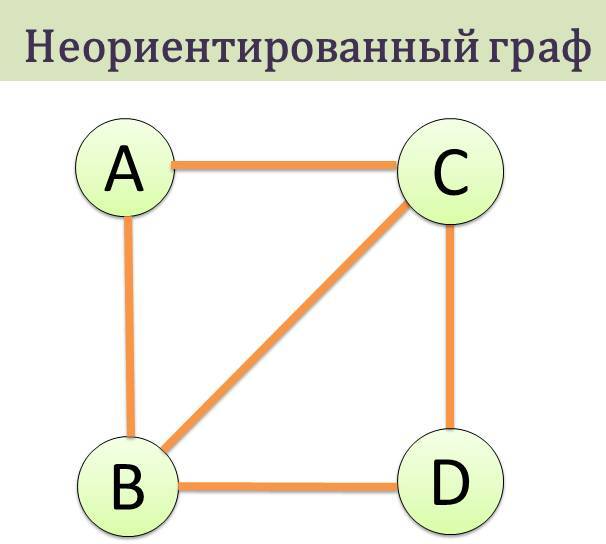
2. Неориентированный граф — это граф, в котором нет направления линий.
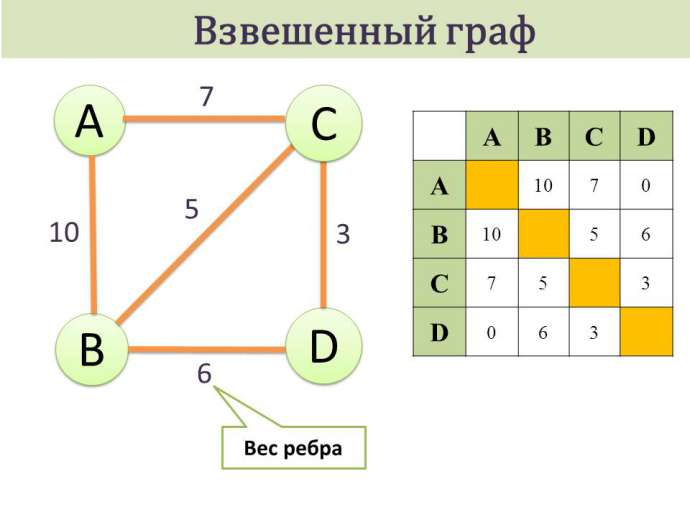
3. Взвешенный граф – дуги или ребра имеют вес (дополнительная информация).
Решение задач с помощью графов:
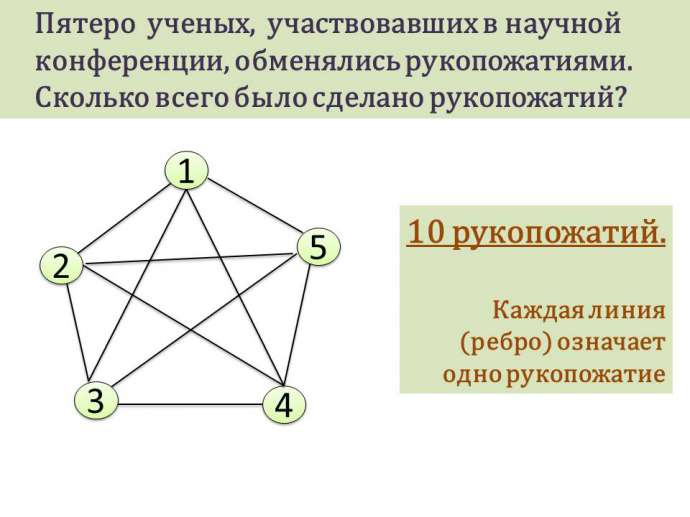
Решение: Обозначим ученых вершинами графа и проведем от каждой вершины линии к четырем другим вершинам. Получаем 10 линий, которые и будут считаться рукопожатиями.
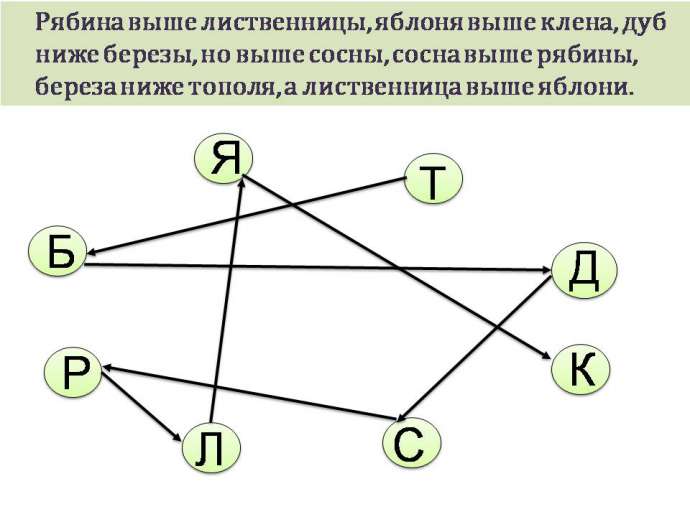
На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Вершины графа — это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.
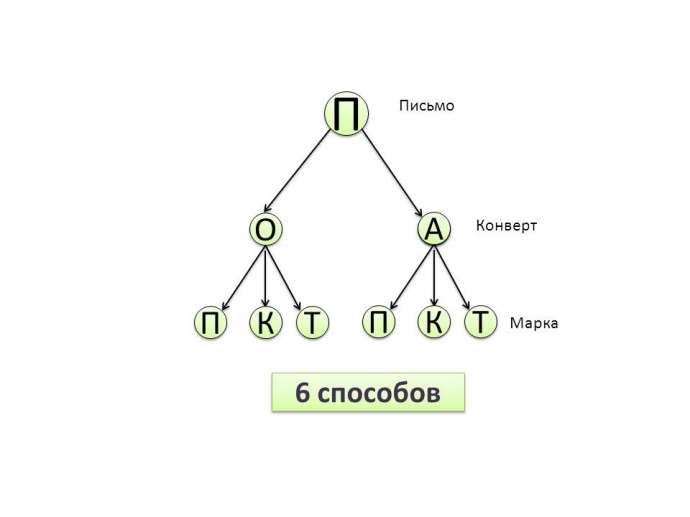
У Наташи есть 2 конверта: обычный и авиа, и 3 марки: прямоугольная, квадратная и треугольная. Сколькими способами Наташа может выбрать конверт и марку, чтобы отправить письмо?
Ниже представлен разбор задач.
Источник