Связность и компоненты графа
Две вершины графа называют связанными, если между ними существует путь. Любая вершина по определению связана сама с собой.
Неорграф называется связным, если любая пара вершин в нем связана. Орграф называется связным, если соответствующий ему неорграф связен. Орграф называется сильно-связным, если для любой пары несовпадающих вершин vi и vj существуют оба маршрута (vi ‑ vj) и (vj ‑ vi).
Бинарное отношение связности в неорграфе (сильной связности в орграфе) является отношением эквивалентности на множестве вершин, поскольку оно рефлексивно, симметрично и транзитивно. И по теореме о разбиении множества на классы эквивалентности, множество вершин графа можно разбить на такие непересекающиеся подмножества, что в каждом из этих подмножеств вершины будут попарно связаны между собой и не связаны с вершинами никаких других подмножеств. Вершинно-порожденные подграфы каждого из подмножеств в этом разбиении называются компонентами графа (сильными компонентами в орграфе). Таким образом, справедливо следующее утверждение: любой неорграф разбивается единственным образом на попарно непересекающиеся компоненты (или, как говорят, в прямую сумму своих компонент, а орграф – в прямую сумму сильных компонент).
На рисунке 26 изображены два графа: неорграф (слева) связным не является и состоит из четырех компонент – , , и . Орграф (справа) связен, но не сильно-связен, имеет три сильные компоненты – , и .
1) Связный граф состоит из одной компоненты, а число компонент в несвязном графе всегда больше единицы.
2) Изолированная вершина является компонентой.
3) В связном графе любые два пути максимальной длины имеют общую вершину.
4) Удаление циклического ребра не нарушает связности графа.
Связный граф без циклов называется деревом. Граф, каждая компонента которого является деревом, называется лесом. На рисунке 27 изображен лес, состоящий из двух деревьев.
Теорема 3.9.1. (Оценка числа ребер в простых графах)
Пусть G =(V, E) – простой граф с в вершинами и k компонентами. Тогда число его ребер р удовлетворяет неравенству:
Доказательство: 1) рассмотрим левую часть неравенства. Если граф связен, то число его компонент k равно 1. Удалим из графа все циклические ребра, в результате этого будет получено дерево. Дальнейшее удаление ребер из дерева будет нарушать связность. Поэтому среди всех связных простых графов дерево имеет наименьшее число ребер. Но число ребер в дереве равно максимальной длине пути, построенного на в вершинах, и по свойствам путей равно (в ‑1). Тем самым, в связном графе число ребер р ³ в ‑1, что совпадает с оценкой снизу при k =1. Пусть теперь G несвязный граф. Тогда он разбивается на k связных компонент, для каждой из которых число ребер рi ³ вi ‑1, где i =1,2,¼, k и рi, вi – это число ребер и вершин в i‑ ой компоненте. Но 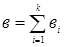
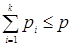
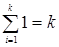
2) Теперь рассмотрим правую часть неравенства (оценку сверху). Если граф связен, то добавим к нему новые ребра, соединяя все пары несмежных вершин. В результате этого будет получен полный граф. Дальнейшее добавление ребер к полному графу будет нарушать его простоту. Поэтому среди всех связных простых графов полный граф имеет наибольшее число ребер. Для подсчета этого числа воспользуемся теоремой о степенях вершин в графе. Поскольку каждая вершина полного графа смежна со всеми остальными его вершинами, то степень каждой вершины равна (в‑ 1), а сумма степеней всех вершин равна в ×(в ‑1). По теореме о степенях вершин это число равно удвоенному числу ребер, поэтому число ребер в полном графе равно 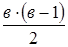
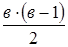
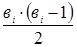
Таким образом, выполненная процедура только увеличивает число ребер. Будем выполнять её над выбранными компонентами до тех пор, пока от j‑ ой компоненты не останется одна изолированная вершина. Затем выберем другую пару компонент с числом вершин больше единицы в каждой. И выполним над этой парой такую же процедуру. И т.д. до тех пор, пока не будет получен граф, в котором с (k ‑1) компонента являются изолированными вершинами и одна компонента – полный граф на (в ‑ k +1) вершинах. Число ребер в полученном графе равно , и оценка сверху доказана.
Следствие. Любой простой граф с в вершинами и числом ребер, большим, чем связен.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
3.9. Деревья и леса
Каждая компонента связности леса – дерево, следовательно, для 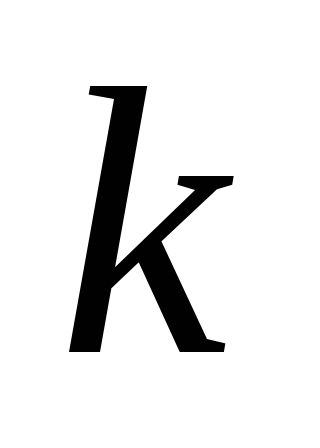

П

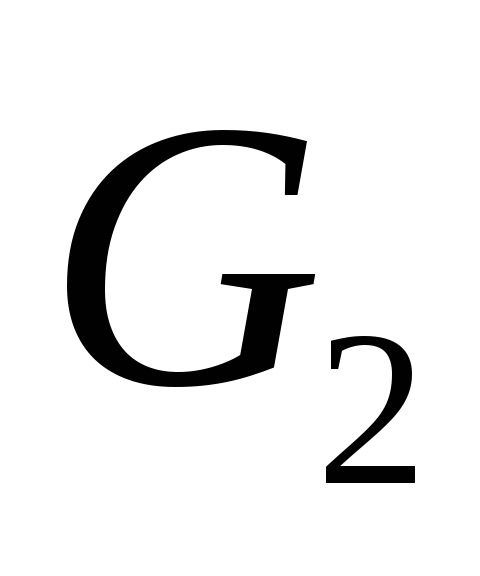

Лемма. Если граф – дерево, то каждое его ребро является мостом.
Доказательство.В параграфе 3.6 было доказано, что если ребро графа не содержится ни в одном цикле, то оно является мостом. Дерево граф ациклический, следовательно, каждое его ребро мост.■
Теорема (основная теорема о деревьях). Для графа следующие утверждения равносильны:
- Граф
— дерево.
ациклический и
.
связный и
.
связный и каждое его ребро является мостом.
- Любые две вершины графа
можно соединить, притом единственной, простой цепью.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
Доказательство.Доказательство проведем по следующей схеме:


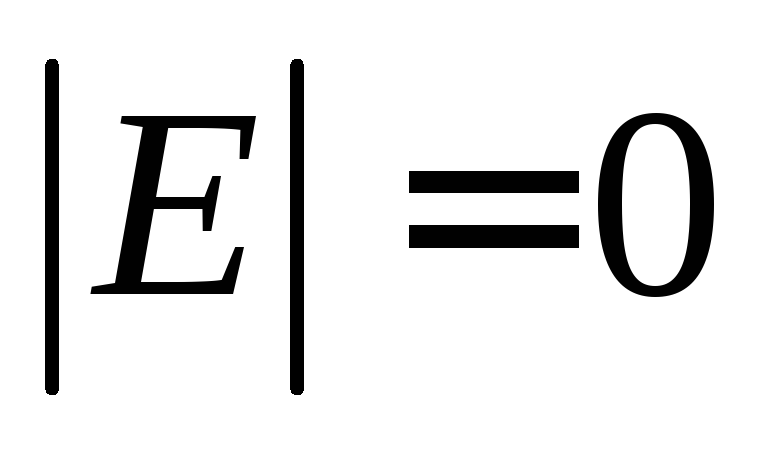
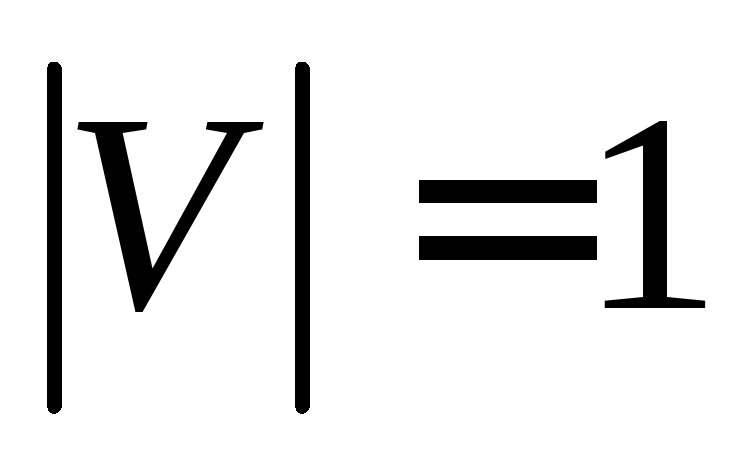
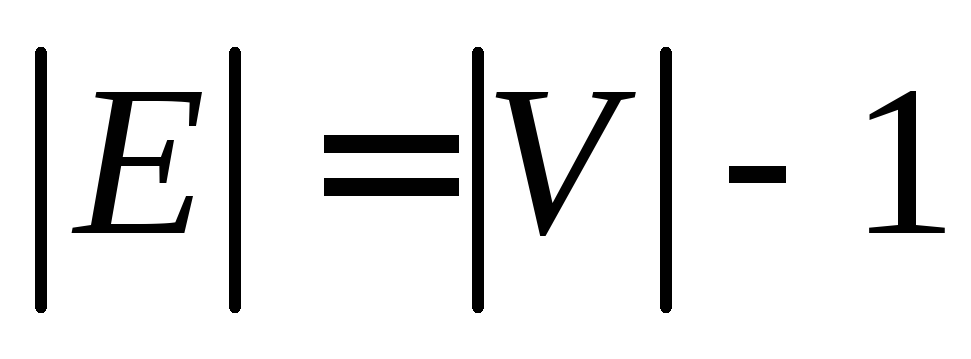




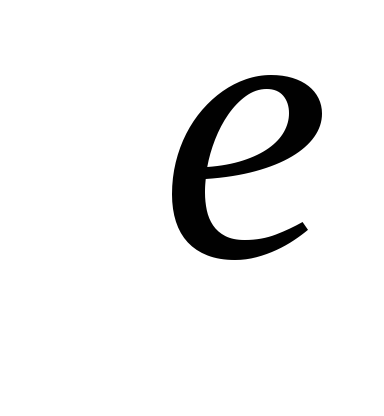
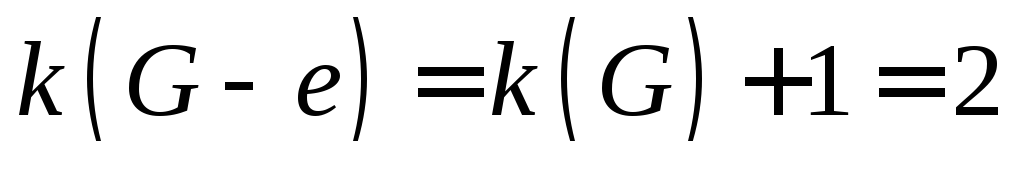
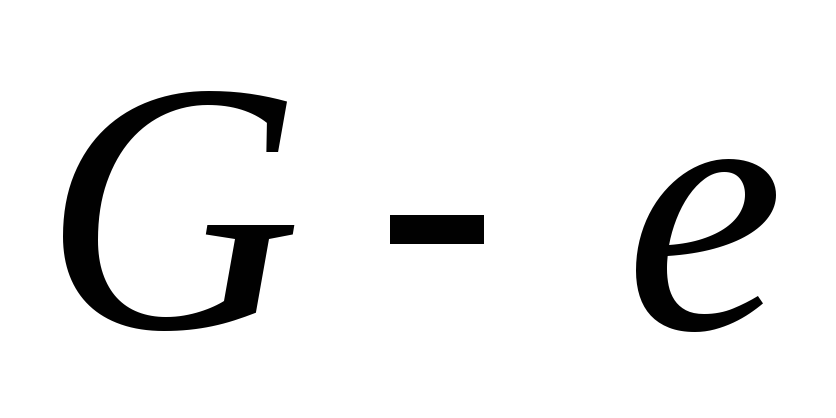
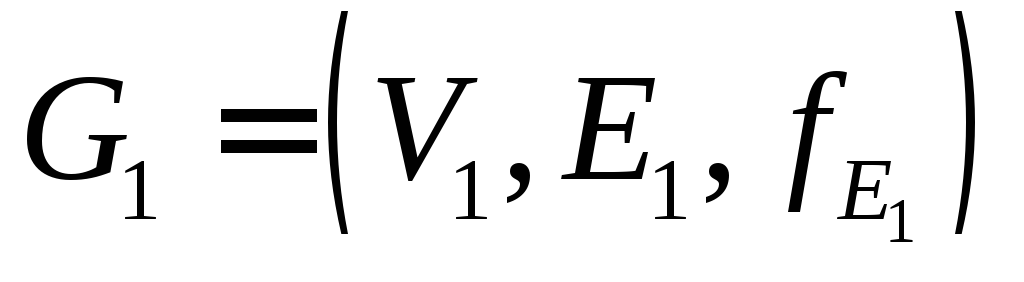
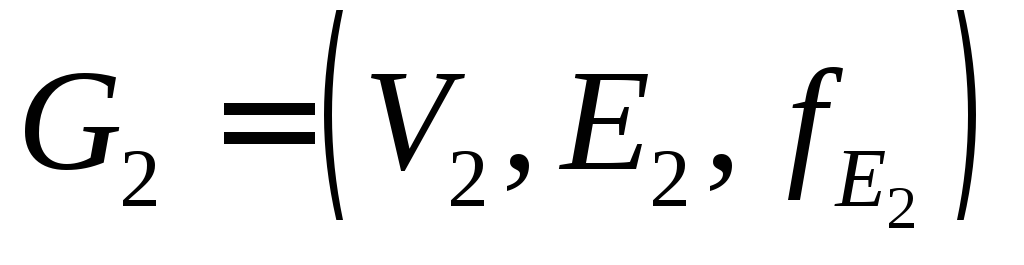
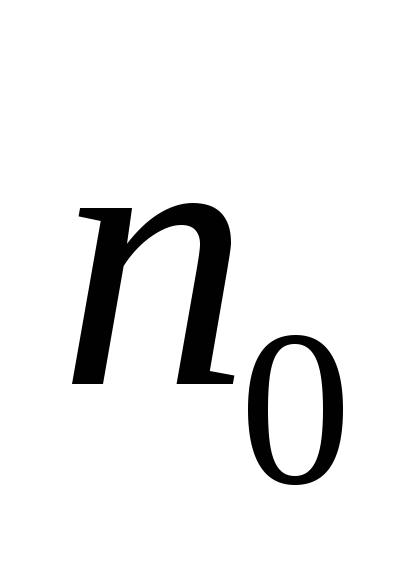
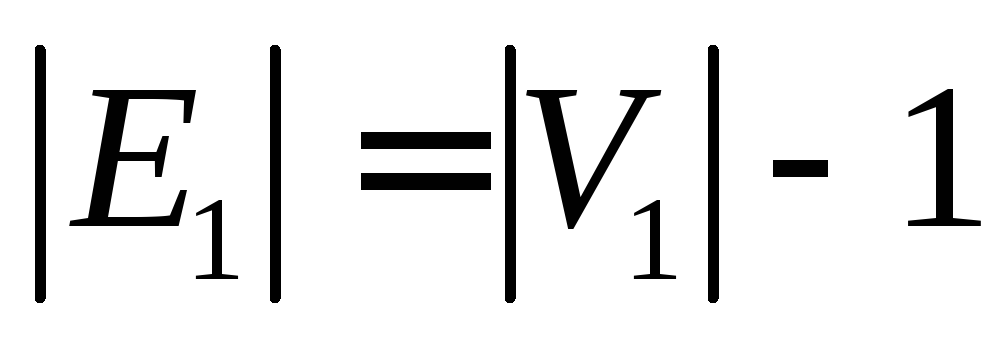
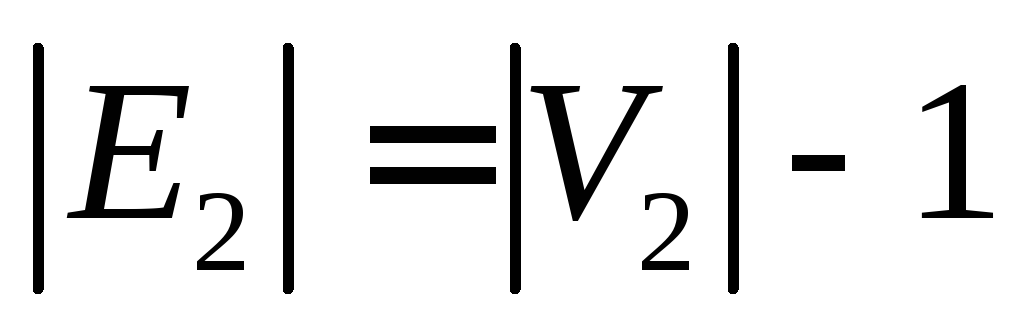



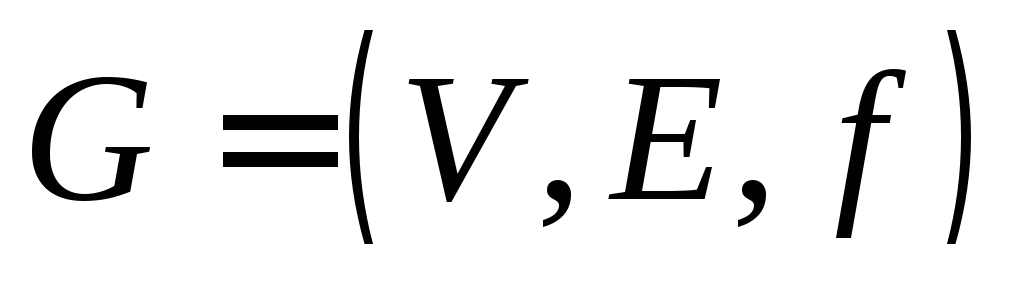
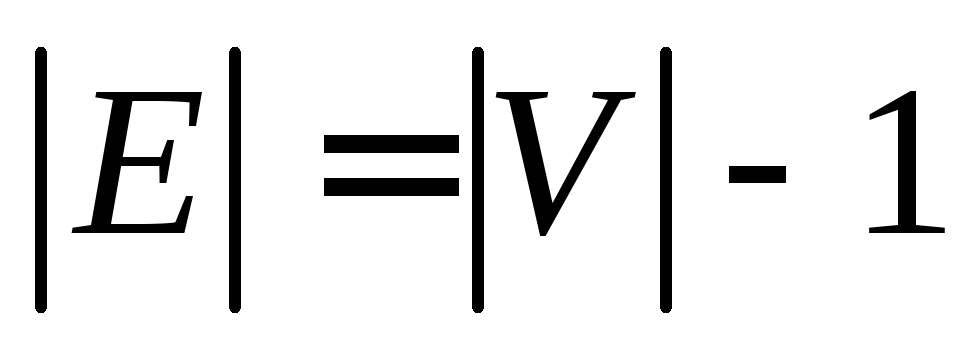

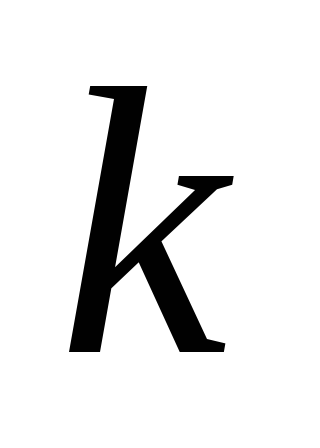











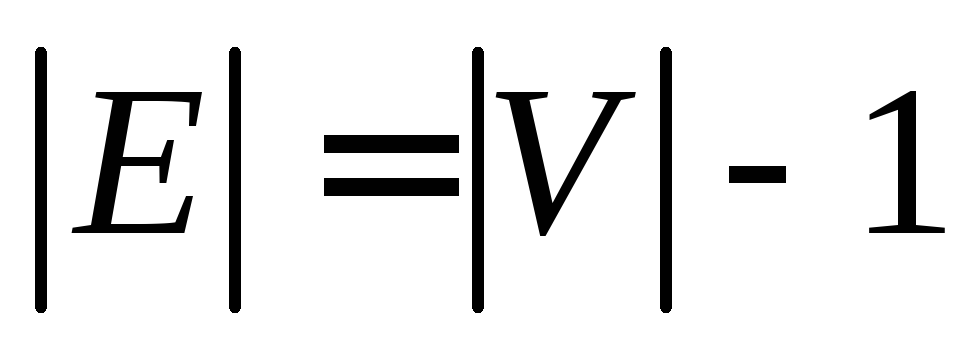



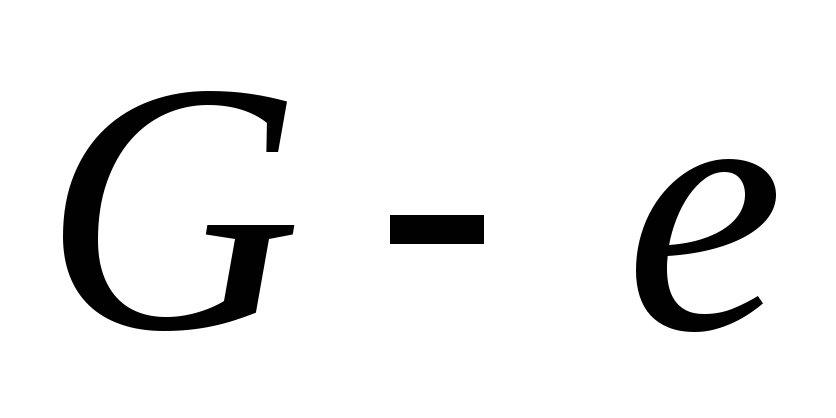
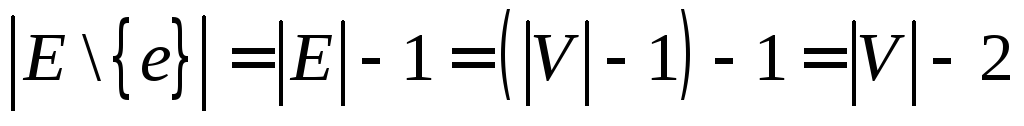
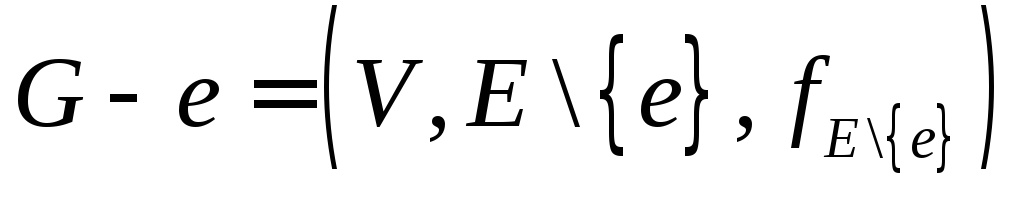



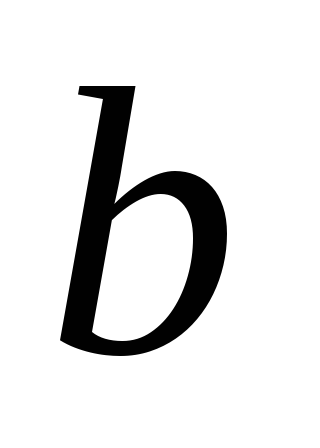








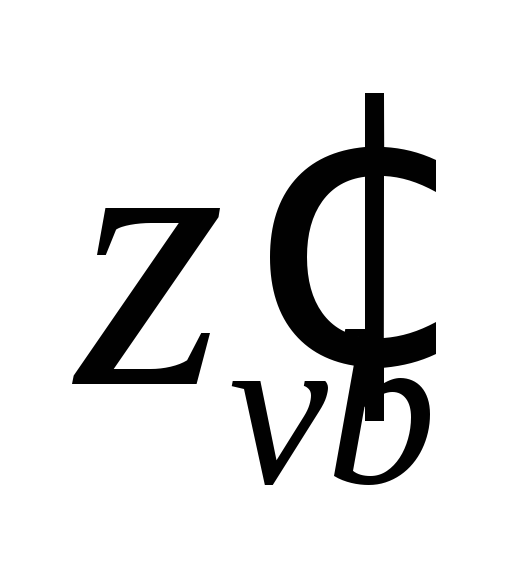
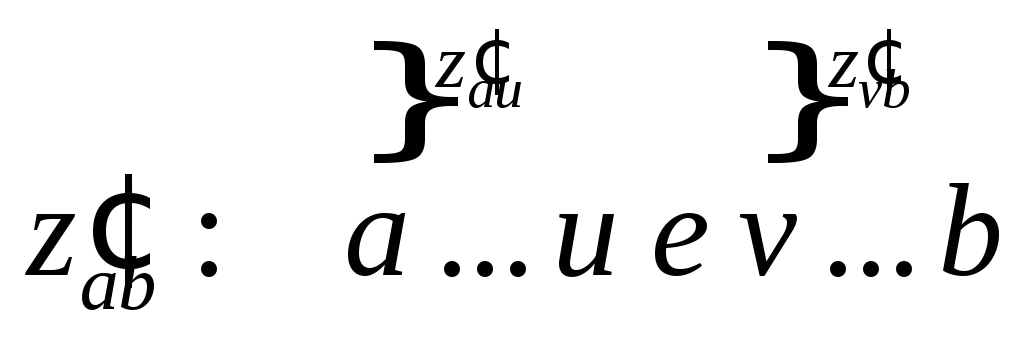



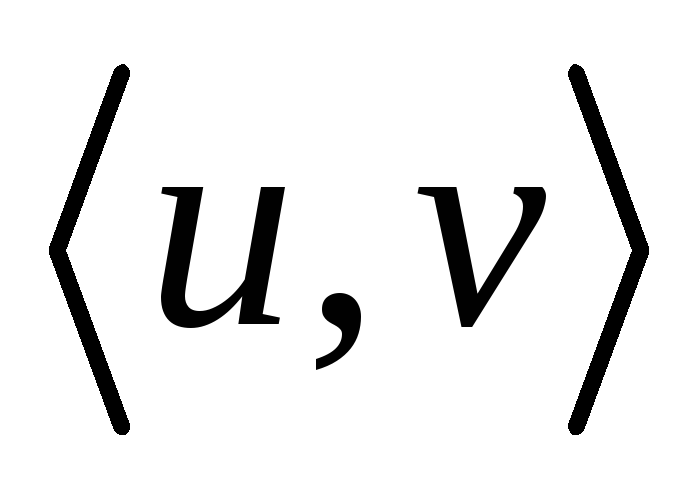

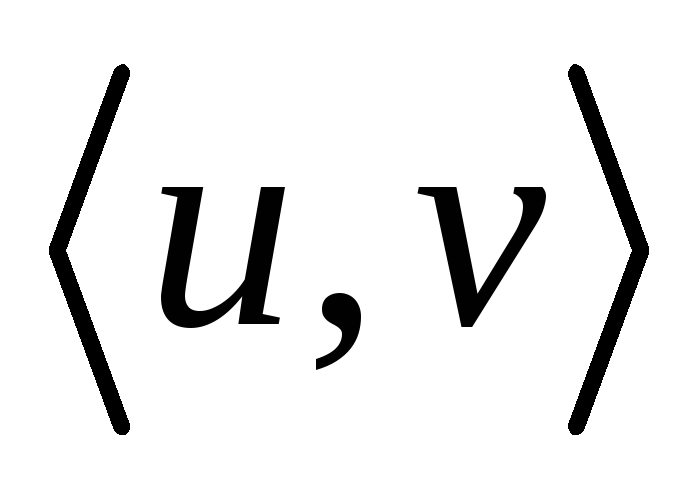
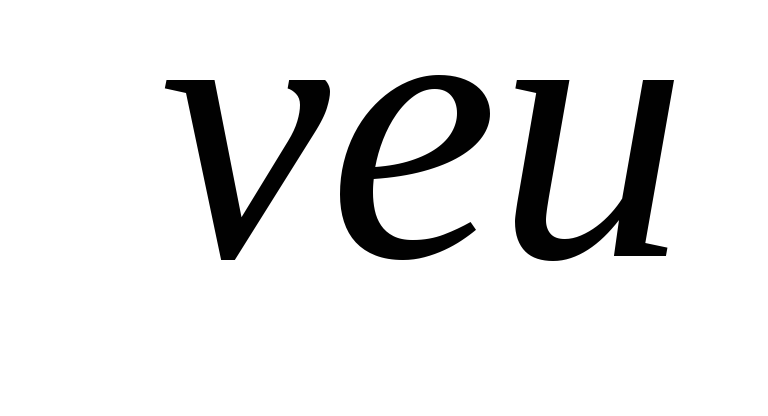

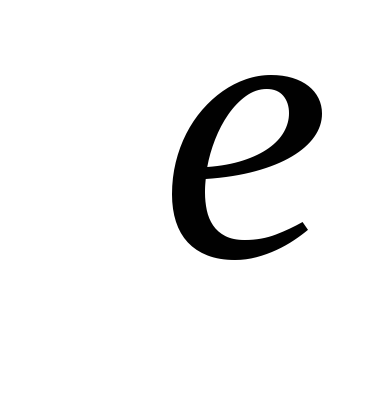






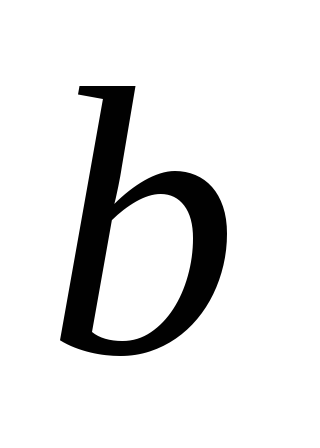







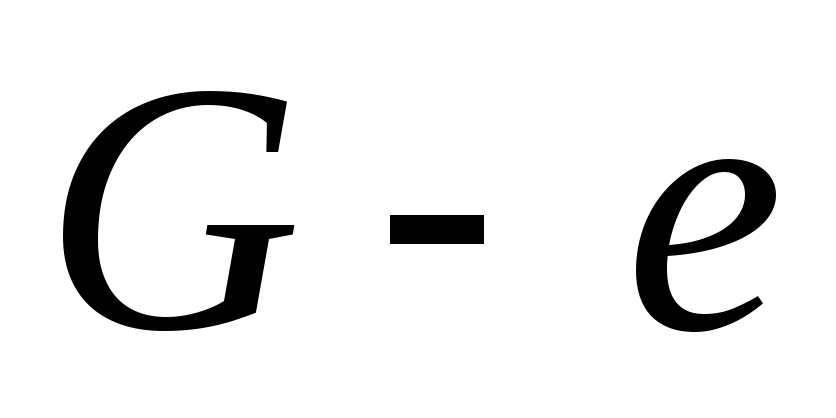

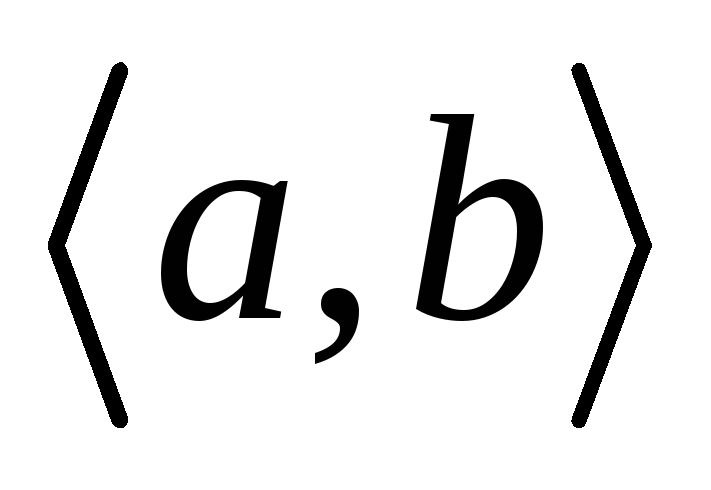
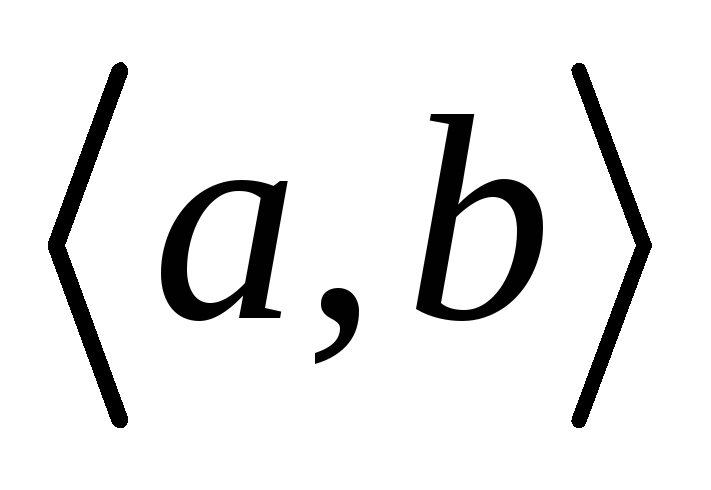



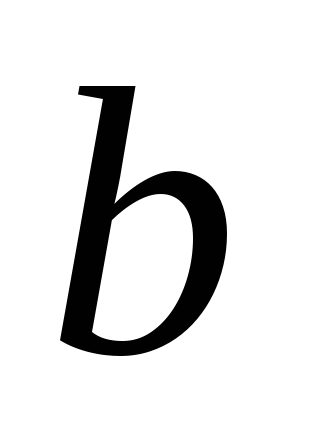





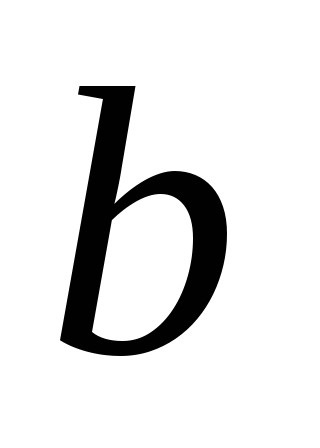
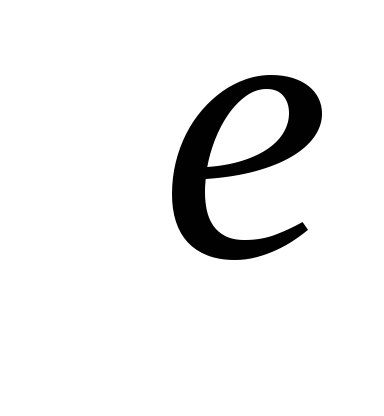
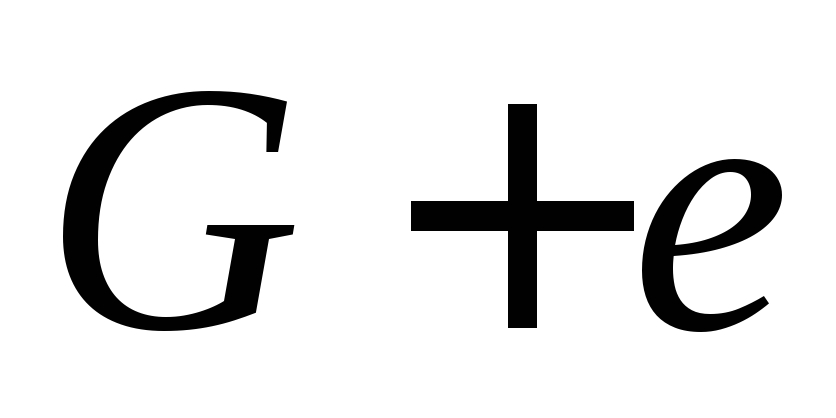

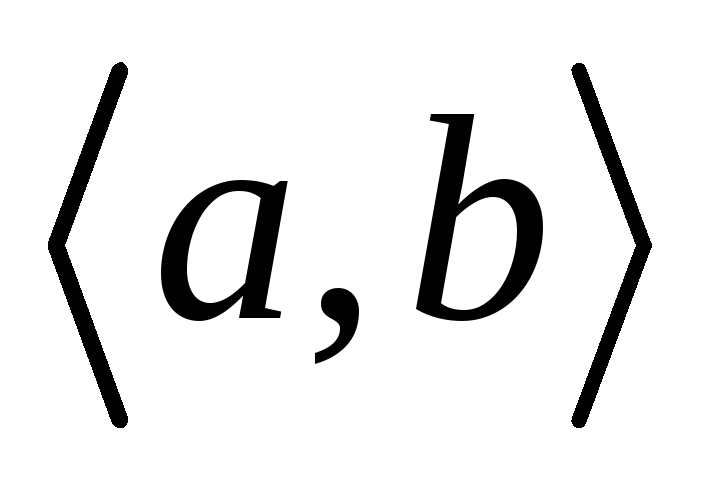

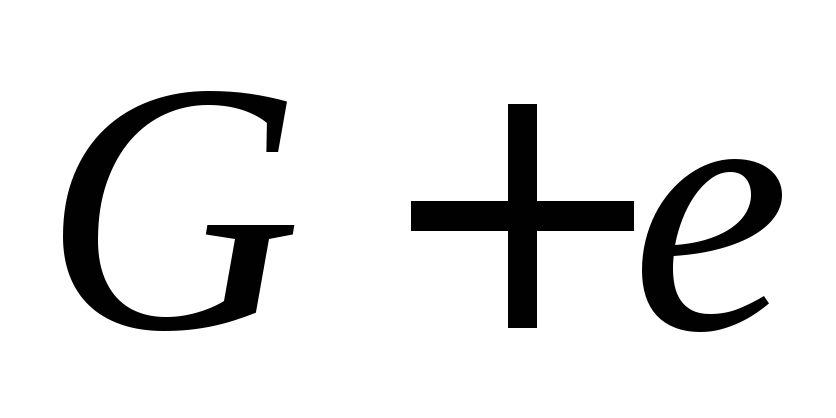
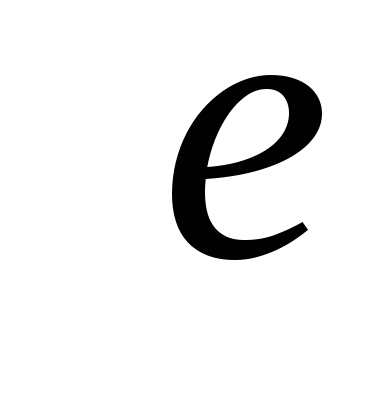
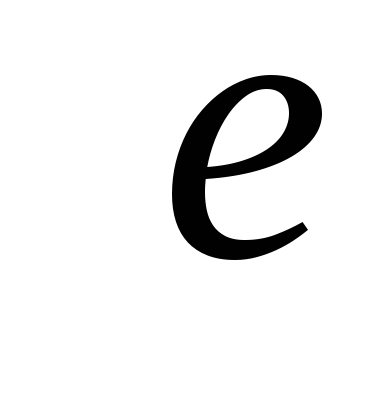

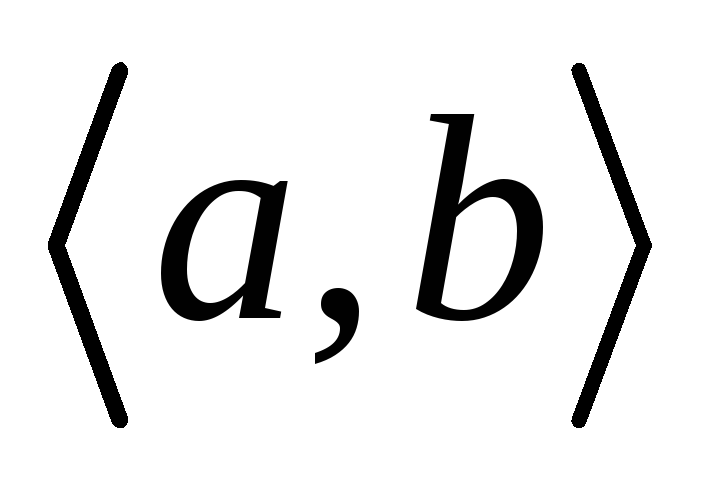







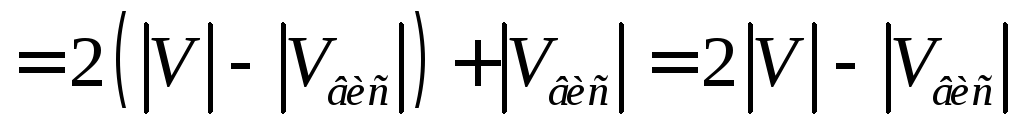




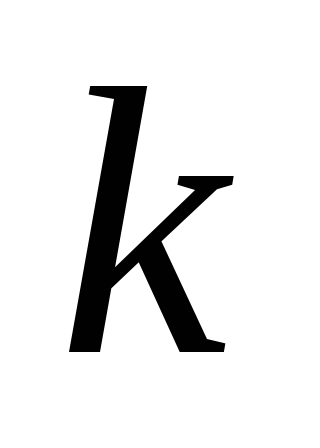

Источник
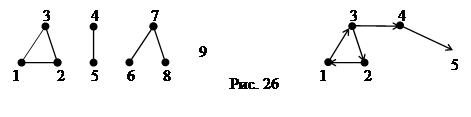
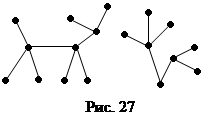
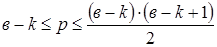
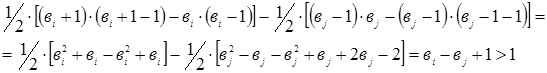
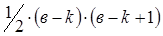
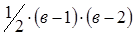

 — дерево.
— дерево. ациклический и
ациклический и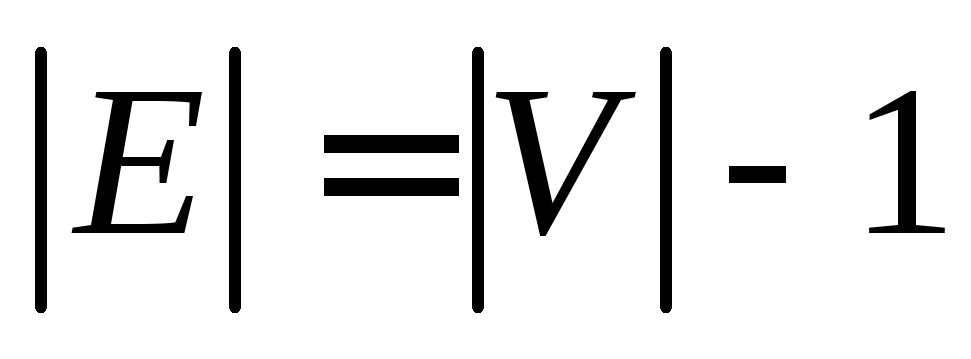 .
. связный и
связный и .
. связный и каждое его ребро является мостом.
связный и каждое его ребро является мостом. можно соединить, притом единственной, простой цепью.
можно соединить, притом единственной, простой цепью. ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.
ациклический, и добавление к нему нового ребра приводит к образованию единственного простого цикла.