Граф задан матрицей смежности дерево

Является ли граф деревом [закрыт]

Закрыт. На этот вопрос невозможно дать объективный ответ. Ответы на него в данный момент не принимаются.

Хотите улучшить этот вопрос? Переформулируйте вопрос так, чтобы на него можно было дать ответ, основанный на фактах и цитатах.

Задачка: Предложите алгоритм, который определяет, является ли граф деревом. Мое решение, которое, как оказалась, неверное

bool is_rec( int arr[SIZE][SIZE], int current, int root, int find ) < bool endFlag = true; for(int i = 0; i < SIZE; ++i)< if((arr[current][i] == 1)&&(i!=root))< if(i!=find)< endFlag = endFlag&&is_rec(arr,i,current,find); >else < return false; >> > return endFlag; > bool IsTree( int arr[SIZE][SIZE] )

4 ответа 4

Дерево — связный граф с n-1 ребром.

bool dfs(int i, int arr[SIZE][SIZE], bool col[SIZE]) < if (col[i]) < return 0; >col[i] = true; for (int j = 0; j < SIZE; ++j) < if (ar[i][j]) < dfs(j, arr, col); >> > bool IsTree(int arr[SIZE][SIZE]) < int edges = 0; for (int i = 0; i < SIZE; ++i) < for (int j = i + 1; j < SIZE; ++j) < if (arr[i][j]) < edges++; >> > if (edges != SIZE - 1) < return false; >bool col[SIZE]; memset(col, 0, sizeof(col)); dfs(0, arr, col); for (int i = 0; i < SIZE; ++i) < if (!col[i]) < return false; >> return true; > 

Моё решение на Pascal. Граф задаётся матрицей смежности (1 — есть ребро, 0 — иначе). maxV — максимальное число вершин maxE — максимальное число рёбер Храню граф списком рёбер.

const maxV = 111; maxE = 111111*2; var n,m,i,j,x : longint; ef,es,next : array [1..maxE] of longint; first,last : array [1..maxV] of longint; c : longint; used : array [1..maxV] of boolean; flag : boolean; procedure add(v1,v2 : longint); begin inc(c); ef[c] := v1; es[c] := v2; if last[v1] <> 0 then next[last[v1]] := c; if first[v1] = 0 then first[v1] := c; last[v1] := c; end; procedure dfs(v,dad : longint); var h,e : longint; begin used[v] := true; h := first[v]; while h > 0 do begin e := es[h]; if used[e] and (e <> dad) then begin flag := false; exit; end; if e <> dad then dfs(e,v); if not flag then exit; h := next[h]; end; end; begin assign(input,'input.txt'); reset(input); assign(output,'output.txt'); rewrite(output); readln(n); for i := 1 to n do for j := 1 to n do begin read(x); if x = 1 then add(i,j); end; flag := true; dfs(1,1); for i := 1 to n do if not used[i] then flag := false; if not flag then writeln('NO') else writeln('YES'); end. 

Источник

Анализ алгоритма

Неориентированный граф, состоящий из n вершин, будет деревом, если он связный и содержит n – 1 ребро. Запускаем поиск в глубину из первой вершины. Если существует обратное ребро, то граф имеет цикл и не является деревом. Одновременно в переменной с подсчитываем количество посещенных вершин в процессе поиска. Если по окончанию поиска в глубину оно не равно n, то граф не является связным.

Граф, приведенный в примере, является деревом.

Матрицу смежности графа храним в массиве m.

Функция dfs реализует поиск в глубину из вершины v. При этом в вершину v мы попали из вершины prev (prev = -1 если v – корень дерева поиска в глубину). В переменной с подсчитываем количество пройденных вершин в процессе поиска.

Ребро (v, i) будет обратным и образовывать цикл, если i ≠ prev и при этом вершина i уже была пройдена раньше (used[ i] = 1).

if (used[i]) flag = 1; else dfs(i,v);

Основная часть программы. Читаем входные данные.

Запускаем поиск в глубину из нулевой вершины. Поскольку она является корнем дерева поиска, то не имеет родителя. В качестве второго аргумента передаем функции dfs значение -1.

Граф не будет деревом, если существует обратное ребро (flag = 1) или граф не является связным (количество посещенных вершин c при поиске в глубину не равно n).

if (flag || (c != n)) printf( «NO\n» ); else printf( «YES\n» );

Если граф является деревом, то:

3. Граф не содержит циклов

Выполнение первых двух условий достаточно для того, чтобы граф являлся деревом.

Java реализация

public class Main

static int c = 0;

static int m [][], used [];

static void dfs( int v )

public static void main(String[] args ) //throws IOException

Scanner con = new Scanner(System. in );

//Scanner con = new Scanner(new FileReader («977.in»));

m = new int [ n ][ n ];

used = new int [ n ];

Arrays.fill( used , 0);

for ( int i = 0; i < n ; i ++)

for ( int j = 0; j < n ; j ++)

m [ i ][ j ] = con .nextInt();

if (( Edges == n — 1) && ( c == n ))

System. out .printf( «YES» );

System. out .printf( «NO» );

Источник

Бинарные деревья

Самым наглядным способом представления информации является ее представление рисунками или графиками. Поэтому при решении многих математических задач используются специальные рисунки (схемы), называемые графами.

Граф представляет собой множество точек – вершин графа, соединенных между собой отрезками – ребрами графа.

Термин граф впервые появился в работах венгерского математика Д.Кенига в 1936 году, хотя ряд задач по теории графов был решен еще Л.Эйлер в XVIII веке.

Примером графа может служить схема линии метрополитена, карта автомобильных или железных дорог. Эти дороги можно рассматривать как ребра, соединяющие города или станции – вершины такого графа.

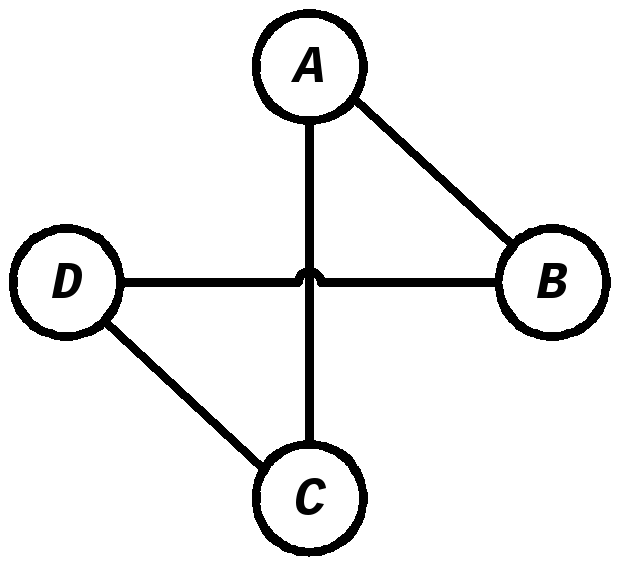
Вершины графа обычно нумеруются или обозначаются прописными латинскими буквами: A. B, C, … Любой граф можно описать или задать перечислением вершин и ребер. Наиболее удобный способ такого задания – с помощью матрицы смежности, в которой строки и столбцы соответствуют вершинам графа, а значения элементов – длине ребер, соединяющих эти вершины. Если длина ребер не задается, то наличие ребра обозначается единицей, а его отсутствие – нулем.

задается матрицей смежности:

Как видно, это симметричная матрица.

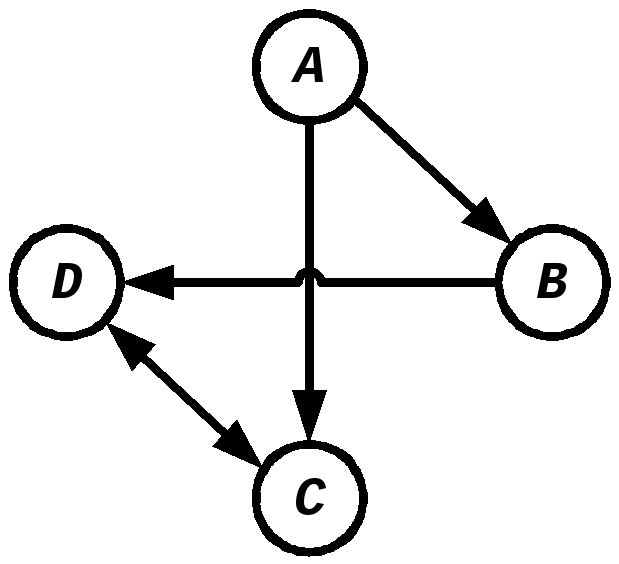
Граф называется ориентированным (орграф), если на каждом его ребре указано направление, то есть о каждой его вершине можно сказать, какие ребра из нее выходят, а какие входят:

Для этого ориентированного графа матрица смежности имеет вид:

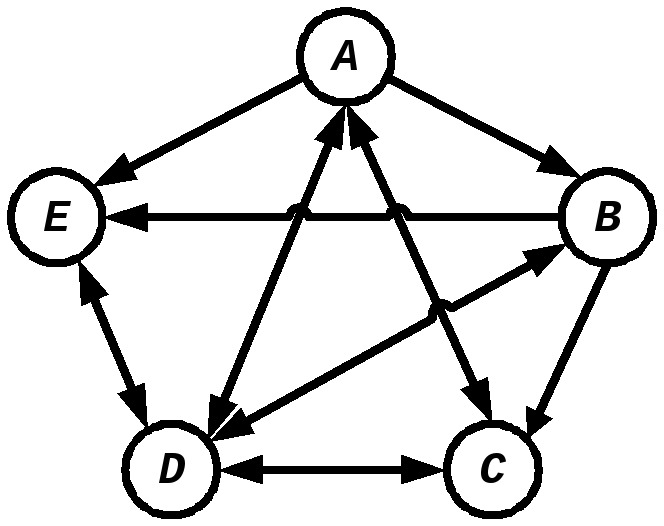
Говорят, что две вершины соединены путем, если из первой вершины можно пройти по ребрам во вторую вершину. Путей между вершинами может быть несколько, поэтому они обозначаются перечислением вершин, которые встречаются на данном пути. Например, вершины A и C графа:

соединены путями ABC, AC, ADC, AEDC, ABDC, AEDBC.

Граф называется связным, если любые две его вершины соединены некоторым путем. Если в графе можно найти замкнутый путь, то граф называется циклическим, а сам замкнутый путь – циклом.

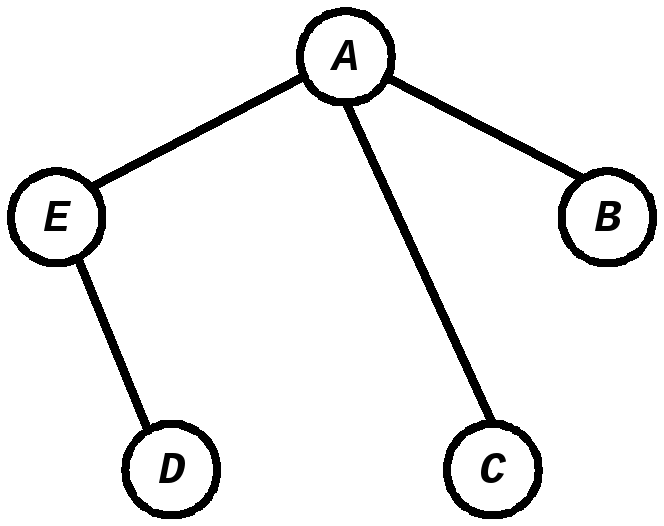
Связный граф, в котором нет циклов, называется деревом:

Одной из основных отличительных черт дерева является то, что в нем любые две вершины соединены единственным путем.

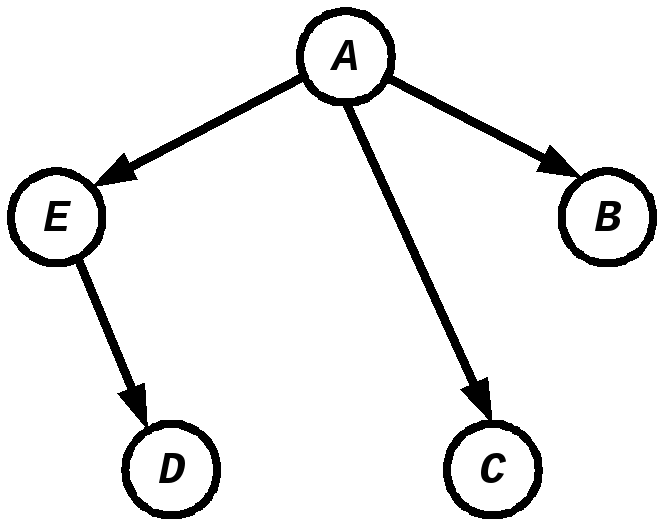
Дерево называется ориентированным, если на каждом его ребре указано направление. Следовательно, о каждой его вершине можно сказать, какие ребра в него входят, а какие из нее выходят. Точно так же о каждом ребре можно сказать, из какой вершины оно выходит, и в какую входит:

Из вершины A выходят три ребра – AB, AC и AЕ, в вершину D входит одно ребро – ED. Этот же граф можно описать следующей матрицей смежности:

A B C D E

В незаполненных ячейках должны стоять нули – связи между соответствующими вершинами нет.

Наименование строки – это имя вершины-источника, из которой ребро выходит, а столбца – вершины-приемника, в которую входит. Таким образом, количество ненулевых элементов в матрице смежности ориентированного графа равно количеству ребер в нем.

Среди деревьев наиболее широкое распространение в программировании получили бинарные деревья.

Бинарное дерево – это такое ориентированное дерево, в котором:

• из каждой вершины исходит не более двух ребер,
• имеется только одна вершина – корень дерева, в которую не входит ни одного ребра,
• в каждую вершину, кроме корня, входит только одно ребро.

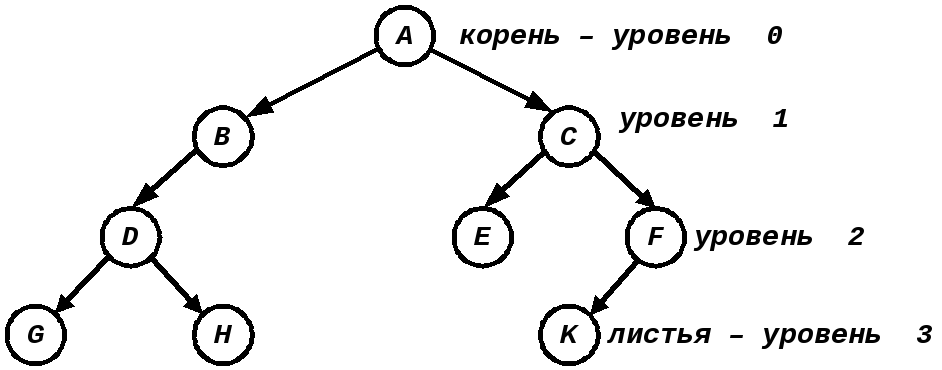
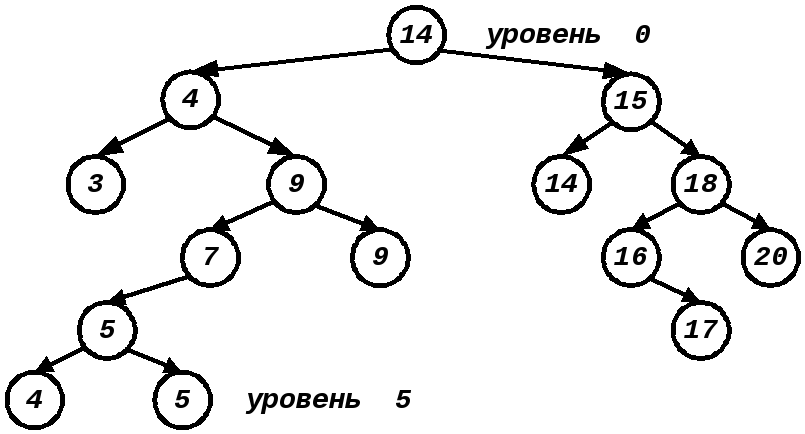
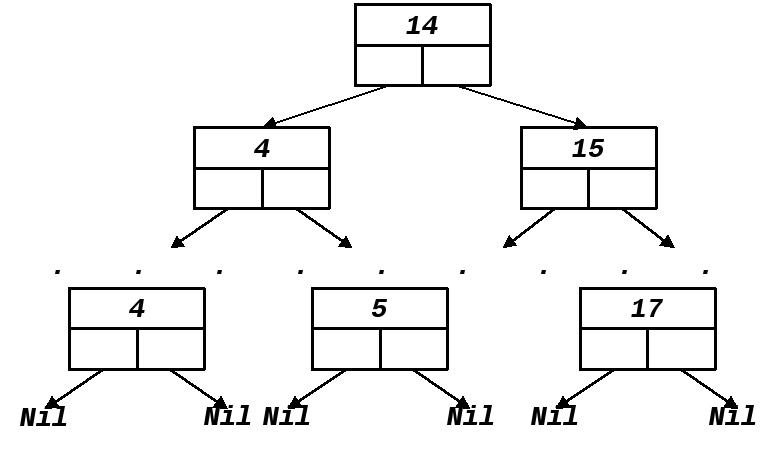
Бинарные деревья обычно изображаются корнем вверх: В этом бинарном дереве вершина A является корнем. Для ребер бинарного дерева, выходящих из одной вершины, имеются две возможности – быть направленными влево-вниз или вправо-вниз: ребро BD направлено влево-вниз, а ребро DH – вправо-вниз. Вершины бинарного дерева называются узлами. Каждый узел можно рассматривать как корень дерева, стоящего ниже него – поддерева, причем различают левое и правое поддеревья. Узел, не являющийся корнем ни одного поддерева, называется листом. В вышеприведенном дереве листьями являются узлы G,H,K. Характеристикой каждого узла является его уровень, определяемый следующим образом: корень дерева имеет нулевой уровень, уровень любого другого узла на единицу больше уровня узла-предшественника: узлы B,C имеют уровень 1, узлы D,E,F – уровень 2, узлы G,H,K (узлы) – уровень 3. Глубина бинарного дерева – это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева. Среди узлов различают предков и потомков: узел A является предком для узлов B и C, узлы G и H – потомками узла D. Поэтому корень дерева – это узел, не имеющий предков, а листья – это узлы, не имеющие потомков. Бинарные деревья – это полезная структура данных в тех случаях, когда в каждой точке вычислительного процесса должно быть принято одно решение из двух возможных (альтернатива), например, в алгоритмах сортировки, когда требуется сравнение каждого очередного элемента (числа, слова) со всеми предшествующими. Использование бинарных деревьев позволяет уменьшить количество таких сравнений: берется первый элемент и помещается в исходный узел бинарного дерева, который становится его корнем с пока пустыми левым и правым поддеревьями. Каждый последующий элемент сравнивается с элементом, стоящим в корне дерева: если новый элемент меньше его, то он образует левый узел следующего уровня, а если больше или равен – то правый. Так продолжается до тех пор, пока сортируемая последовательность элементов не закончится. При этом получается, что самый левый лист будет содержать минимальный элемент из введенной последовательности, а самый правый – максимальный. Любой левый узел будет содержать элемент, меньший, чем элемент в предшествующем узле, а правый – больший или равный элементу в предшествующем узле. Например, следующая последовательность чисел: 14 15 4 9 7 18 3 5 16 4 20 17 9 14 5 образует бинарное дерево: В этом дереве самый левый лист содержит наименьшее число 4, а самый правый – наибольшее 20. Если сейчас просмотреть это дерево в так называемом симметричном порядке – слева направо: левое поддерево — его корень – правое поддерево, то получим отсортированную последовательность: 3 4 4 5 5 7 9 9 14 14 15 16 17 18 20 Бинарное дерево можно представить связным списком, в котором каждое ссылочное поле каждого элемента (узла) должно содержать значения двух ссылок – на элемент (узел) слева внизу и элемент (узел) справа внизу. Если один из узлов отсутствует, то ссылка на него равна Nil. Самые нижние элементы списка (листья) имеют ссылки со значениями Nil: Если информационные поля элементов дерева являются данными целого типа, то дерево можно описать, например, следующим образом: Type TRebro = ^TUzel;TUzel = RecordData:Integer;информационное полеLeft,Right:TRebro;ссылочные поляEnd;

Источник

О деревьях

Аннотация: Представления деревьев. Представление с помощью матрицы смежности. Представление с помощью списков смежности. Представление с помощью списка ребер и кода Прюфера. Алгоритм построения кода Прюфера. Алгоритм раскодирования. Уровневые коды корневых деревьев. Перечисление и подсчет деревьев. Непомеченные деревья. Ориентированные деревья. Каркасы в неориентированном графе. Каркасы в ориентированных графах.

Представления деревьев

Каждому дереву можно поставить в соответствие некоторый код. С помощью этого кода можно восстановить дерево с точностью до изоморфизма . Существуют различные способы кодировки деревьев, которые позволяют решать конкретные задачи (подсчет деревьев, установление изоморфизма , генерирование всех неизоморфных деревьев и т.д.). Представлением дерева называется способ записи информации о нем, однозначно и полностью восстанавливающий структуру дерева и позволяющий вычислить его характеристики. Выбор представления зависит от решаемой задачи и способа ее решения. Рассмотрим наиболее распространенные способы задания деревьев.

Представление с помощью матрицы смежности

Это представление является общим для всех видов графов; оно задает граф с точностью до изоморфизма , но вместе с тем данное представление неэкономично, так как ненулевыми являются для -вершинного дерева только из

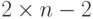
Для неориентированного графа матрица смежности симметрична относительно главной диагонали, поэтому можно задавать только верхнюю треугольную половину матрицы, но это не улучшает ситуацию. Другой недостаток этого представления заключается в том, что трудоемкость алгоритмов, работающих с таким представлением, не может быть ниже.