Оптимизация производительности дерева решений
Как вы можете видеть выше, дерево слишком обширно и не так точно. Это дерево также требует времени, поэтому для лучших результатов нам нужно оптимизировать дерево путем настройки параметра. Здесь я объясню только важный параметр Алгоритма дерева решений, для его настройки потребуется новый пост в блоге. Если вы посмотрите на параметры DecisionTreeClassifier может взять, вы можете быть удивлены, давайте посмотрим на некоторые из них.
критерий:Этот параметр определяет, как будет измеряться степень загрязнения. Значением по умолчанию является «Джини», но вы также можете использовать «энтропию» в качестве метрики для примесей.
разветвитель:Вот как дерево решений ищет функции для разделения. Значение по умолчанию установлено на «лучший». То есть для каждого узла алгоритм учитывает все функции и выбирает наилучшее разбиение. Если вы решите установить параметр разделителя на «случайный», то будет рассматриваться случайное подмножество объектов. Разделение будет затем выполнено наилучшей функцией в случайном подмножестве. Размер случайного подмножества определяется параметром max_features. Это частично, где Случайный Лес получает свое имя.
Максимальная глубина:Это определяет максимальную глубину дерева. В нашем случае мы используем глубину два, чтобы сделать наше дерево решений. По умолчанию установлено значение none. Это часто приводит к переопределенным деревьям решений. Параметр глубины является одним из способов, которыми мы можем упорядочить дерево или ограничить его рост, чтобы предотвратитьнад-фитинга,
min_samples_split:Минимальное количество выборок, которое должен содержать узел, чтобы рассмотреть расщепление. Значение по умолчанию равно двум. Вы можете использовать этот параметр, чтобы упорядочить ваше дерево.
min_samples_leaf:Минимальное количество выборок необходимо считать листовым узлом. Значение по умолчанию установлено в единицу. Используйте этот параметр, чтобы ограничить рост дерева.
max_features:Количество функций, которые следует учитывать при поиске лучшего разделения. Если это значение не установлено, дерево решений будет учитывать все функции, доступные для наилучшего разделения. В зависимости от вашего приложения, часто бывает полезно настроить этот параметр.
В целях синтаксиса, давайте установим некоторые из этих параметров:
Setting parameterstree = DecisionTreeClassifier(criterion = "entropy", splitter = "random", max_depth = 2, min_samples_split = 5,min_samples_leaf = 2, max_features = 2).fit(X,y)
Дополнительно: переоснащение и недостаточное оснащение
На практике дерево нередко имеет 10 разбиений между верхним уровнем (все данные) и листом. По мере того как дерево становится глубже, набор данных разбивается на листья с меньшим количеством данных. Если у дерева было только 1 разбиение, оно делит данные на 2 группы. Если каждая группа будет разделена снова, мы получим 4 группы данных. Разделение каждого из них снова создаст 8 групп. Если мы продолжим удваивать количество групп, добавляя больше разбиений на каждом уровне, к моменту перехода на 10-й уровень у нас будет 210 210 групп данных. Это 1024 листа.
Когда мы делим данные между многими листами, у нас также меньше данных на каждом листе. Листья с очень небольшим количеством данных сделают прогнозы, которые достаточно близки к фактическим значениям этих домов, но они могут сделать очень ненадежные прогнозы для новых данных (потому что каждое предсказание основано только на нескольких данных).
Это явление называетсяпереобучениягде модель почти полностью соответствует обучающим данным, но плохо проверяет и другие новые данные. С другой стороны, если мы сделаем наше дерево очень поверхностным, оно не разделит данные на очень четкие группы.
В крайнем случае, если дерево делит данные только на 2 или 4, каждая группа по-прежнему имеет широкий спектр данных. Результирующие прогнозы могут быть далеки от большинства данных, даже в данных обучения (и по той же причине они будут плохими в валидации). Когда модель не может зафиксировать важные различия и закономерности в данных, поэтому она плохо работает даже в обучающих данных, это называетсяunderfitting,
Поскольку мы заботимся о точности новых данных, которые мы оцениваем на основе наших данных валидации, мы хотим найти точку отсчета между недостаточным и избыточным соответствием Визуально нам нужна нижняя точка (красной) кривой проверки на изображении, показанном ниже.
Это все, ребята. Счастливого обучения . 🙂
Источник
8.10. Метод «дерево решений»
Для анализа рисков инновационных проектов часто применяют метод дерева решений. Он предполагает, что у проекта существует несколько вариантов развития. Каждое решение, принимаемое по проекту, определяет один из сценариев его дальнейшего развития. При помощи дерева решений решаются задачи классификации и прогнозирования. Дерево решений – это схематическое представление проблемы принятия решений. Ветви дерева решений представляют собой различные события (решения), а его вершины – ключевые состояния, в которых возникает необходимость выбора. Чаще всего дерево решений является нисходящим, т. е. строится сверху вниз. Выделяют следующие этапы построения дерева решений:
- Первоначально обозначают ключевую проблему. Это будет вершина дерева.
- Для каждого момента определяют все возможные варианты дальнейших событий, которые могут оказать влияние на ключевую проблему. Это будут исходящие от вершины дуги дерева.
- Обозначают время наступления событий.
- Каждой дуге прописывают денежную и вероятностную характеристики.
- Проводят анализ полученных результатов.
Основа наиболее простой структуры дерева решений – ответы на вопросы «да» и «нет». Пример 1. Рассмотрим пример дерева решений, задача которого – ответить на вопрос «Пойти ли гулять?». Чтобы решить эту задачу, необходимо ответить на ряд вопросов, которые находятся в узлах дерева (рис. 8.1). Вершина дерева «На улице солнечно» является узлом проверки. Если на этот вопрос получен положительный ответ, то переходим к левой ветви дерева, если отрицательный – то к правой. Движение продолжается до тех пор, пока не будет получен окончательный ответ.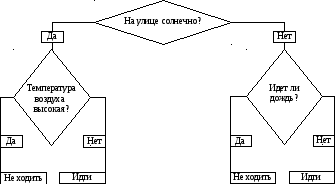 
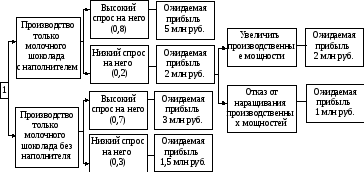
Рис. 8.1. Дерево решений «пойти ли гулять» Для каждой дуги дерева могут быть определены числовые характеристики, например величина прибыли по проекту и вероятность ее получения. В этом случае оно помогает учесть все возможные варианты действия и соотнести с ними финансовые результаты. Для формулирования сценариев развития проекта необходимо располагать достоверной информацией с учетом вероятности и времени наступления событий. Затем переходят к сравнению альтернатив. Пример 2. Компания «Конфетти» в настоящее время выпускает плитки молочного шоколада. Директор по развитию считает, что на рынке повысился спрос на молочный шоколад с наполнителями. Перед компанией стоит вопрос: переходить ли на производство молочного шоколада с наполнителем или не стоит этого делать? Если производить шоколад обоих типов, то потребуется увеличить производственные мощности. Информация об ожидаемых выигрышах и вероятности событий в случае того или иного решения представлена на дереве решений (рис. 8.2). Используя дерево решений, руководитель находит наиболее предпочтительное решение – увеличить производственные мощности. Это обусловлено ожидаемой прибылью – 2 млн руб., которая превышает прибыль 1 млн руб. при отказе от такого наращивания, если в точке «а» будет низкий спрос. Руководитель, двигаясь к первой точке принятия решения, рассчитывает предполагаемую прибыль в случае альтернативных действий. 
Рис. 8.2. Дерево решений «какой шоколад производить» Для производства только молочного шоколада с наполнителем она составит 4,4 млн руб. (5 × 0,8 + 0,2 × 2). Аналогично рассчитывается ожидаемое значение для варианта выпуска только молочного шоколада без наполнителя, которое равно всего 2,55. Таким образом, наращивание производственных мощностей является наиболее желательным решением и приносит наибольший выигрыш. Пример 3. Руководителю отдела нужно принять решение относительно закупки станков. Второй станок более экономичный, но и в то же время более дорогой и требует больших накладных расходов (рис. 8.3). Руководителю нужно выбрать тот станок, который обеспечит максимизацию прибыли.
| Оборудование | Постоянные расходы | Операционный расход на единицу техники |
| Станок 1 | 500 000 | 670 |
| Станок 2 | 700 000 | 940 |
Рис. 8.3. Дерево решений Руководитель оценивает вероятность спроса на продукцию, производимую на станках:
- 2 000 ед. с вероятностью 0,4;
- 3 000 ед. с вероятностью 0,6.
Станок 1: 840 000 × 0,4 + 1 510 000 × 0,6 = 1 242 000. Станок 2: 1 180 000 × 0,4 + 2 120 000 × 0,6 = 1 744 000. Таким образом, приобретение второго станка более экономично. Недостатками дерева решений является ограниченное число вариантов решения проблемы. В процессе построения дерева решений необходимо обращать внимание на его размер. Оно не должно быть слишком перегруженным, т. к. это уменьшает способность к обобщению и способность давать верные ответы.
Источник